Câu hỏi:
22/07/2024 137Tìm tập hợp các số nguyên n để \[A = \frac{{3n - 5}}{{n + 4}}\]có giá trị là số nguyên.
A. n∈{13}
B. n∈{−21; −5; −3; 13}
C. n∈{−17; −1; 1; 17}
D. n∈{−13; −3; 3; 13}
Trả lời:
Giải bởi Vietjack
Ta có:
\[A = \frac{{3n - 5}}{{n + 4}}\]
\[ = \frac{{3n + 12 - 12 - 5}}{{n + 4}}\]
\[ = \frac{{3\left( {n + 4} \right) + \left( { - 17} \right)}}{{n + 4}}\]
\[ = \frac{{3\left( {n + 4} \right)}}{{n + 4}} + \frac{{ - 17}}{{n + 4}}\]
\[ = 3 + \frac{{ - 17}}{{n + 4}}\]
Vì n∈Z nên để A∈Z thì n+4∈U(−17) = {±1; ±17}
Ta có bảng:
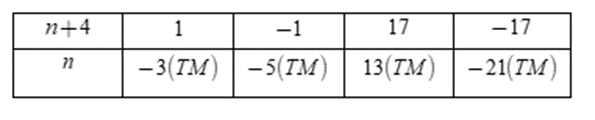
Vậy n∈{−21; −5; −3; 13}
Đáp án cần chọn là: B
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Có bao nhiêu giá trị nguyên dương của n để \[\frac{9}{{4n + 1}}\] đạt giá trị nguyên.
Câu 6:
Cho tập A = {1; −2; 3; 4}. Có bao nhiêu phân số có tử số và mẫu số thuộc A mà có tử số khác mẫu số và tử số trái dấu với mẫu số?
Câu 8:
Cho biểu thức \[C = \frac{{11}}{{2n + 1}}\]. Tìm tất cả các giá trị của n nguyên để giá trị của C là một số tự nhiên.
Câu 9:
Có bao nhiêu cặp số nguyên (x; y) thỏa mãn \[\frac{x}{5} = \frac{3}{y}\] và x >y?
Câu 10:
Cho các phân số: \[\frac{{15}}{{60}};\frac{{ - 7}}{5};\frac{6}{{15}};\frac{{28}}{{ - 20}};\frac{3}{{12}}\]. Số cặp phân số bằng nhau trong những phân số trên là:
Câu 12:
Tổng các số a, b, c thỏa mãn \[\frac{6}{9} = \frac{{12}}{a} = \frac{b}{{ - 54}} = \frac{{ - 738}}{c}\] là:
Câu 13:
Tìm x; y biết \[\frac{{x - 4}}{{y - 3}} = \frac{4}{3}\]và x – y = 5.
