Câu hỏi:
22/07/2024 137Cho biểu thức \[C = \frac{{11}}{{2n + 1}}\]. Tìm tất cả các giá trị của n nguyên để giá trị của C là một số tự nhiên.
A. n∈{−6; −1; 0; 5}
B. n∈{−1; 5}
C. n∈{0; 5}
D. n∈{1; 11}
Trả lời:
Giải bởi Vietjack
Vì C∈N nên C∈Z. Do đó ta tìm n∈Z để C∈Z
Vì n∈Z nên để C∈Z thì 2n+1∈U(11) = {±1; ±11}
Ta có bảng:
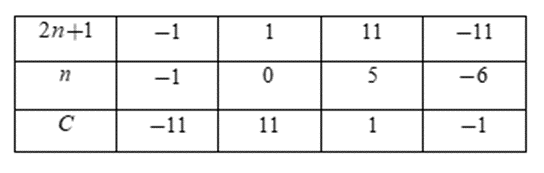
Vì C∈N nên ta chỉ nhận các giá trị n = 0; n = 5
Đáp án cần chọn là: C
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Có bao nhiêu giá trị nguyên dương của n để \[\frac{9}{{4n + 1}}\] đạt giá trị nguyên.
Câu 5:
Cho tập A = {1; −2; 3; 4}. Có bao nhiêu phân số có tử số và mẫu số thuộc A mà có tử số khác mẫu số và tử số trái dấu với mẫu số?
Câu 8:
Tìm tập hợp các số nguyên n để \[A = \frac{{3n - 5}}{{n + 4}}\]có giá trị là số nguyên.
Câu 9:
Có bao nhiêu cặp số nguyên (x; y) thỏa mãn \[\frac{x}{5} = \frac{3}{y}\] và x >y?
Câu 10:
Cho các phân số: \[\frac{{15}}{{60}};\frac{{ - 7}}{5};\frac{6}{{15}};\frac{{28}}{{ - 20}};\frac{3}{{12}}\]. Số cặp phân số bằng nhau trong những phân số trên là:
Câu 12:
Tổng các số a, b, c thỏa mãn \[\frac{6}{9} = \frac{{12}}{a} = \frac{b}{{ - 54}} = \frac{{ - 738}}{c}\] là:
Câu 13:
Tìm x; y biết \[\frac{{x - 4}}{{y - 3}} = \frac{4}{3}\]và x – y = 5.
