Câu hỏi:
18/07/2024 194Tập hợp các điểm cách đều ba đỉnh của tam giác ABC là:
A. tâm đường tròn ngoại tiếp tam giác ABC.
B. tâm đường tròn nội tiếp tam giác ABC.
C. đường thẳng vuông góc với mặt phẳng (ABC) và đi qua tâm đường tròn ngoại tiếp tam giác ABC.
D. đường thẳng vuông góc với mặt phẳng (ABC) và đi qua tâm đường tròn nội tiếp tam giác ABC.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
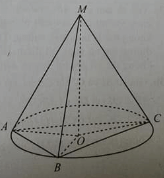
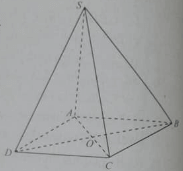
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, MO là đường thẳng vuông góc với mặt phẳng (ABC) tại O.
Ta có: OA, OB, OC lần lượt là hình chiếu của các đường xiên MA, MB, MC.
Vì OA = OB = OC
⇒ MA = MB = MC.
Vậy đường thẳng MO là tập hợp các điểm cách đều ba đỉnh A, B, C của tam giác ABC.
Đáp án C
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD, đáy là hình thoi tâm O và SA = SC, SB = SD
Đường thẳng AC vuông góc với mặt phẳng
Câu 3:
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa CM với mặt phẳng (BCD) bằng:
Câu 6:
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa AC với mặt phẳng (ABD) bằng:
Câu 8:
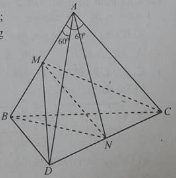
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng . Gọi M, N là trung điểm của AB và CD.
Đường thẳng CD vuông góc với mặt phẳng
Câu 9:
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng DB không vuông góc với đường thẳng nào sau đây?
Câu 10:
Cho hình tứ diện ABCD có ba cạnh AB, BC, CD đôi một vuông góc.
Đường thẳng AB vuông góc với :
Câu 11:
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng BC vuông góc với đường thẳng
Câu 13:
Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ (ABCD) Tam giác SBC là:
Câu 14:
Cho hình lập phương ABCD. A’B’C’D’. Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
Câu 15:
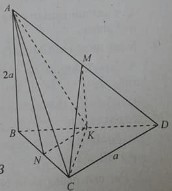
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Gọi M là trung điểm của AD và K là trung điểm của BD
Góc giữa CM với mặt phẳng (BCD) là: