Câu hỏi:
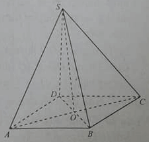
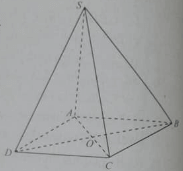
18/07/2024 1,358Cho hình chóp S.ABCD, đáy là hình thoi tâm O và SA = SC, SB = SD
Đường thẳng AC vuông góc với mặt phẳng
A. (SAC)
B. (SBD)
C. (ABCD)
D. (SDC)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
* Xét tam giác SAC có SA = SC nên tam giác cân tại S.
Lại có, SO là đường trung tuyến nên đồng thời là đường cao: (1)
* Vì đáy ABCD là hình thoi nên: (2)
Mà SO và BD là 2 đường thẳng cắt nhau, cùng thuộc mp (SBD) (3)
Từ (1); (2); (3) suy ra:
Đáp án B
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
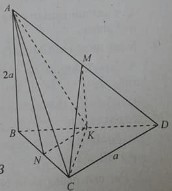
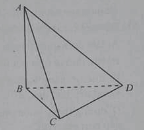
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa CM với mặt phẳng (BCD) bằng:
Câu 5:
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Tan của góc giữa AC với mặt phẳng (ABD) bằng:
Câu 7:
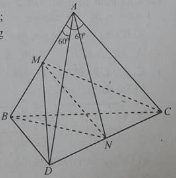
Cho tứ diện ABCD có AB = AC = AD; góc BAC bằng góc BAD bằng . Gọi M, N là trung điểm của AB và CD.
Đường thẳng CD vuông góc với mặt phẳng
Câu 8:
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng DB không vuông góc với đường thẳng nào sau đây?
Câu 9:
Cho hình tứ diện ABCD có ba cạnh AB, BC, CD đôi một vuông góc.
Đường thẳng AB vuông góc với :
Câu 10:
Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng BC vuông góc với đường thẳng
Câu 13:
Cho hình chóp S.ABCD có ABCD là hình vuông và SA ⊥ (ABCD) Tam giác SBC là:
Câu 14:
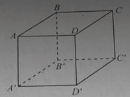
Cho hình lập phương ABCD. A’B’C’D’. Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:
Câu 15:
Cho tứ diện ABCD có BCD là tam giác đều cạnh bằng a, AB vuông góc với (BCD) và AB = 2a.
Gọi M là trung điểm của AD và K là trung điểm của BD
Góc giữa CM với mặt phẳng (BCD) là: