Một mặt cầu ngoại tiếp hình lập phương cạnh a. Tính diện tích mặt cầu đó

Đáp án đúng: A

*Lời giải:

Do hình lập phương cạnh a nên bán kính khối cầu = a 

Diện tích mặt cầu = 4.pi.a²

*Phương pháp giải:

- Tính bán kính khối cầu 

- Áp dụng công thức tính thể tích khối cầu để tính: S=4.pi.R² 

${}^{}$

Diện tích mặt cầu và thể tích khối cầu

Cho mặt cầu S(I; R).

Diện tích mặt cầu: $S=4\pi R^2$

Thể tích khối cầu: $V=\frac{4}{3}\pi R^3$

Dạng 1: Mặt cầu ngoại tiếp hình chóp

* Phương pháp giải:

- Xác định trục d của đường tròn ngoại tiếp đa giác đáy (d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).

- Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục ∆ của đường tròn ngoại tiếp một đa giác của mặt bên).

- Giao điểm I của (P) và d (hoặc của ∆ và d) là tâm mặt cầu ngoại tiếp.

- Kết luận: I là tâm mặt cầu ngoại tiếp chóp.

Dạng 1.1: Hình chóp có các điểm cùng nhìn một cạnh của hình chóp dưới một góc vuông.

+) Hình chóp tam giác:

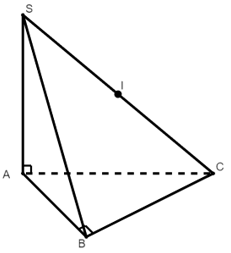
A, B cùng nhìn SC dưới một góc vuông

Tâm mặt cầu ngoại tiếp hình chóp S.ABC là trung điểm I của SC

Bán kính là: $R=\frac{SC}{2}$

+) Hình chóp tứ giác

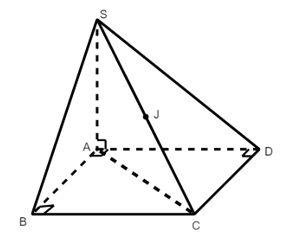
A, B, D cùng nhìn SC dưới một góc vuông

Tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm J của SC

Bán kính mặt cầu là: $R=\frac{SC}{2}$

Dạng 1.2: Hình chóp có mặt bên vuông góc với mặt phẳng đáy

* Phương pháp giải: Gọi h là chiều cao hình chóp và $R_b,R_d$ là bán kính của đường tròn ngoại tiếp mặt bên, mặt đáy và $\partial$ là độ dài cạnh chung của mặt bên vuông góc với đáy thì bán kính mặt cầu là:

$R=\sqrt{{R_b}^2+{R_d}^2-{\left(\frac{\partial }{2}\right)}^2}$

Dạng 1.3: Mặt cầu nội tiếp khối đa diện

* Phương pháp giải: Nếu đặt V là thể tích khối chóp và $S_{tp}$ là tổng diện tích mặt đáy và các mặt bên của chóp thì bán kính r của mặt cầu nội tiếp khối chóp: $r=\frac{3V}{S_{tp}}$

Xem thêm các bài viết liên quan hay, chi tiết

Bài tập Mặt cầu Toán 12

Các bài toán thực tế hình không gian (có đáp án)

Phương trình mặt cầu (lý thuyết và cách giải các dạng bài tập)