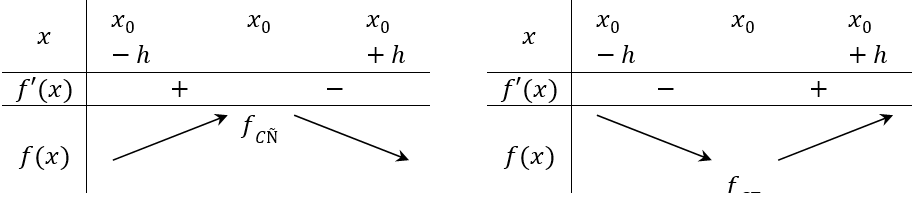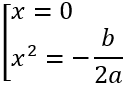Hàm số nào sau đây không có cực trị?

Đáp án đúng: D

*Lời giải:

 

$\Rightarrow$nên hàm số không có cực trị

*Phương pháp giải:

- Để xét điểm cực trị hàm số, ta sẽ: 

   Bước 1. Tìm tập xác định của hàm số.

   Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.

   Bước 3. Lập bảng biến thiên.

   Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.

* Các lý thuyết thêm và các dạng bài toán về cực trị hàm số:

1.Định nghĩa: Cho hàm số y = f(x)xác định và liên tục trên khoảng (a;b) (có thể a là -∞; b là +∞) và điểm x0∈(a;b).

Nếu tồn tại số h > 0 sao cho f(x)< f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x≠x_0 thì ta nói hàm số f(x) đạt cực đại tại x0.

Nếu tồn tại số h >0 sao cho f(x) >f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x ≠ x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.

2.Điều kiện đủ để hàm số có cực trị: Giả sử hàm số y=f(x) liên tục trên

K=(x0 - h;x0 + h)và có đạo hàm trên K hoặc trên K\{x0}, với h >0.

Nếu f'(x)> 0 trên khoảng (x0 - h;x0) và f'(x) <0 trên (x0;x0 + h) thì x0 là một điểm cực đại của hàm số f(x).

Nếu f'(x) < 0 trên khoảng (x0 - h;x0) và f'(x) >0 trên (x0;x0+ h) thì x0 là một điểm cực tiểu của hàm số f(x).

Minh họa bằng bảng biến thiến

Chú ý.

Nếu hàm sốy=f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCÑ (fCT), còn điểm M(x0;f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

DẠNG 1:Tìm cực trị của hàm số

Quy tắc 1:

   Bước 1. Tìm tập xác định của hàm số.

   Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.

   Bước 3. Lập bảng biến thiên.

   Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.

Quy tắc 2:

   Bước 1. Tìm tập xác định của hàm số.

   Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệuxi (i=1,2,3,...)là các nghiệm của nó.

   Bước 3. Tính f''(x) và f''(xi ) .

   Bước 4. Dựa vào dấu của f''(xi )suy ra tính chất cực trị của điểm xi.

DẠNG 2:Tìm tham số m để hàm số đạt cực trị tại một điểm 

Trong dạng toán này ta chỉ xét trường hợp hàm số có đạo hàm tại x0.

Khi đó để giải bài toán này, ta tiến hành theo hai bước.

Bước 1. Điều kiện cần để hàm số đạt cực trị tại x0 là y'(x0) = 0, từ điều kiện này ta tìm được giá trị của tham số .

Bước 2. Kiểm lại bằng cách dùng một trong hai quy tắc tìm cực trị ,để xét xem giá trị của tham số vừa tìm được có thỏa mãn yêu cầu của bài toán hay không?

DẠNG 3:Biện luận theo m số cực trị của hàm số

1. Cực trị của hàm số bậc ba

Cho hàm số y = ax3 + bx2 + cx + d, a ≠ 0.

y' = 0 ⇔ 3ax2 + 2bx + c = 0 (1) ; Δ'y' = b2 - 3ac

    Phương trình (1) vô nghiệm hoặc có nghiệm kép thì hàm số đã cho không có cực trị.

    Hàm số bậc 3 không có cực trị ⇔ b2 - 3ac ≤ 0

    Phương trình (1) có hai nghiệm phân biệt thì hàm số đã cho có 2 cực trị.

     Hàm số bậc 3 có 2 cực trị ⇔ b2 - 3ac > 0

2. Cực trị của hàm số bậc bốn trùng phương

Cho hàm số: y = ax4 + bx2 + c (a ≠ 0) có đồ thị là (C).

y' = 4ax3 + 2bx; y' = 0 ⇔ 

    (C)có một điểm cực trị y' = 0 có 1 nghiệm x = 0 ⇔ -b/2a ≤ 0 ⇔ ab ≥ 0.

    (C)có ba điểm cực trị y' = 0 có 3 nghiệm phân biệt ⇔ -b/2a > 0 ⇔ ab < 0.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Cực trị của hàm số (mới 2024 + Bài Tập) – Toán 12 

Cực trị của hàm số và cách giải các dạng bài tập (2024) mới nhất 

Trắc nghiệm Cực trị của hàm số có đáp án (P1) (Vận dụng)