Câu hỏi:
17/07/2024 101
Hai đường thẳng phân biệt a và b cắt nhau tại điểm O. Trên a, b lấy lần lượt hai điểm M, N khác O. Gọi (P) là mặt phẳng đi qua ba điểm M, N, O (Hình 25). Mặt phẳng (P) có chứa cả hai đường thẳng a và b không? Giải thích.
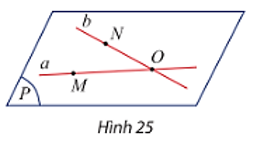
Hai đường thẳng phân biệt a và b cắt nhau tại điểm O. Trên a, b lấy lần lượt hai điểm M, N khác O. Gọi (P) là mặt phẳng đi qua ba điểm M, N, O (Hình 25). Mặt phẳng (P) có chứa cả hai đường thẳng a và b không? Giải thích.

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có:
Hai điểm O và M thuộc mặt phẳng (P) nên đường thẳng a thuộc (P).
Hai điểm O và N thuộc mặt phẳng (P) nên đường thẳng b thuộc (P).
Vậy mặt phẳng (P) chứa cả hai đường thẳng a và b.
Ta có:
Hai điểm O và M thuộc mặt phẳng (P) nên đường thẳng a thuộc (P).
Hai điểm O và N thuộc mặt phẳng (P) nên đường thẳng b thuộc (P).
Vậy mặt phẳng (P) chứa cả hai đường thẳng a và b.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
c) Gọi N là một điểm tùy ý trên cạnh AB. Tìm giao điểm của đường thẳng MN và mặt phẳng (SBD).
c) Gọi N là một điểm tùy ý trên cạnh AB. Tìm giao điểm của đường thẳng MN và mặt phẳng (SBD).
Câu 4:
Cho bốn điểm A, B, C, D phân biệt, trong đó không có ba điểm nào thẳng hàng. Có bao nhiêu đường thẳng đi qua hai trong bốn điểm đã cho.
Cho bốn điểm A, B, C, D phân biệt, trong đó không có ba điểm nào thẳng hàng. Có bao nhiêu đường thẳng đi qua hai trong bốn điểm đã cho.
Câu 5:
Cho hai đường thẳng a và b cắt nhau tại O và điểm M không thuộc mặt phẳng (a, b).
a) Tìm giao tuyến của hai mặt phẳng (M, a) và (M, b).
Cho hai đường thẳng a và b cắt nhau tại O và điểm M không thuộc mặt phẳng (a, b).
a) Tìm giao tuyến của hai mặt phẳng (M, a) và (M, b).
Câu 6:
Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D).
a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD), (EFG) và (ACD).
Cho tứ diện ABCD. Gọi E, F, G lần lượt là ba điểm trên ba cạnh AB, AC, BD sao cho EF cắt BC tại I (I ≠ C), EG cắt AD tại H (H ≠ D).
a) Tìm giao tuyến của các mặt phẳng (EFG) và (BCD), (EFG) và (ACD).
Câu 7:
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?

b) Tìm diểm giống nhau của các hình trong Hình 31.
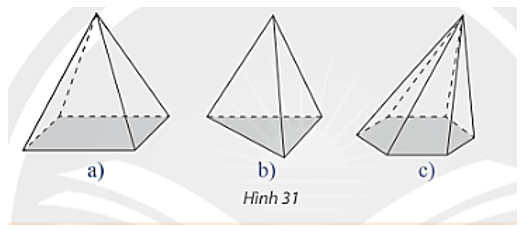
a) Các công trình kiến trúc, đồ vật trong Hình 30 có mặt bên là hình gì?

b) Tìm diểm giống nhau của các hình trong Hình 31.

Câu 8:
Cho mặt phẳng (Q) đi qua bốn đỉnh của tứ giác ABCD. Các điểm nằm trên đường chéo của tứ giác ABCD có thuộc mặt phẳng (Q) không? Giải thích.
Cho mặt phẳng (Q) đi qua bốn đỉnh của tứ giác ABCD. Các điểm nằm trên đường chéo của tứ giác ABCD có thuộc mặt phẳng (Q) không? Giải thích.
Câu 9:
c) Gọi I, J, K lần lượt là giao điểm của QM và AB, QP và AC, QN và AD. Chứng minh I, J, K thẳng hàng.
c) Gọi I, J, K lần lượt là giao điểm của QM và AB, QP và AC, QN và AD. Chứng minh I, J, K thẳng hàng.
Câu 11:
Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Lấy M, N lần lượt thuộc các cạnh SA, SC.
a) Chứng minh đường thẳng MN nằm trong mặt phẳng (SAC).
Cho hình chóp S.ABCD, gọi O là giao điểm của AC và BD. Lấy M, N lần lượt thuộc các cạnh SA, SC.
a) Chứng minh đường thẳng MN nằm trong mặt phẳng (SAC).
Câu 12:
c) Lấy điểm A’ trên đoạn MA và điểm B’ trên đoạn MB sao cho đường thẳng A’B’ cắt mp(a, b) tại C. Chứng minh ba điểm A, B, C thẳng hàng.
c) Lấy điểm A’ trên đoạn MA và điểm B’ trên đoạn MB sao cho đường thẳng A’B’ cắt mp(a, b) tại C. Chứng minh ba điểm A, B, C thẳng hàng.
Câu 13:
Cho đường thẳng a và điểm A không nằm trên a. Trên a lấy hai điểm B, C. Đường thẳng a có nằm trong mặt phẳng (ABC) không? Giải thích.
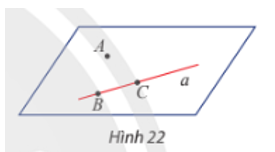
Cho đường thẳng a và điểm A không nằm trên a. Trên a lấy hai điểm B, C. Đường thẳng a có nằm trong mặt phẳng (ABC) không? Giải thích.

Câu 14:
Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà. Tìm giao tuyến của mặt phẳng tạo bởi các tia laser OA và OB của các mặt tường trong Hình 29.
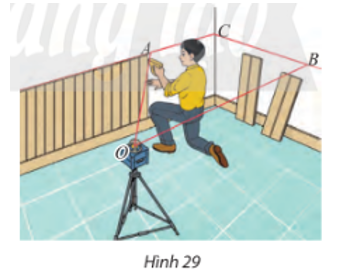
Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà. Tìm giao tuyến của mặt phẳng tạo bởi các tia laser OA và OB của các mặt tường trong Hình 29.

Câu 15:
Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không.
Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không.



