Câu hỏi:
16/07/2024 626
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng (−π;3π2) để:
Hàm số y = tanx nhận giá trị bằng ‒1;
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng (−π;3π2) để:
Hàm số y = tanx nhận giá trị bằng ‒1;
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Xét đồ thị hàm số y = ‒1 và đồ thị hàm số y = tanx trên khoảng (−π;3π2):
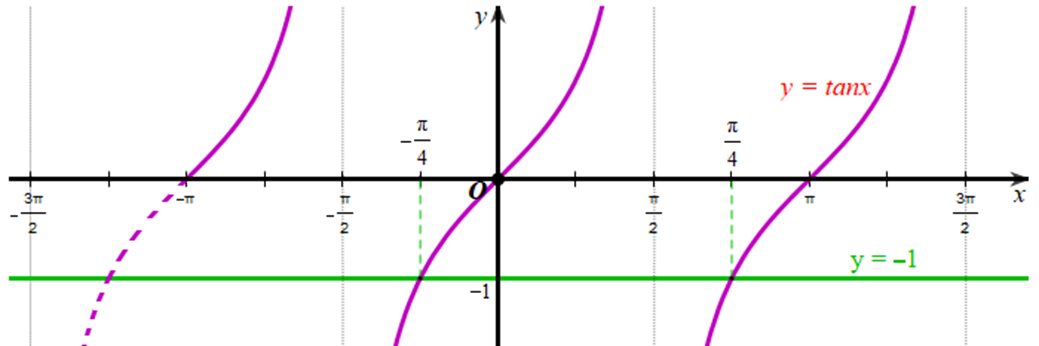
Quan sát đồ thị của hai hàm số, ta thấy hàm số y = tanx trên khoảng (−π;3π2) nhận giá trị bằng ‒1 tại x∈{−π4;π4}.
Xét đồ thị hàm số y = ‒1 và đồ thị hàm số y = tanx trên khoảng (−π;3π2):

Quan sát đồ thị của hai hàm số, ta thấy hàm số y = tanx trên khoảng (−π;3π2) nhận giá trị bằng ‒1 tại x∈{−π4;π4}.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Quan sát đồ thị hàm số y = cotx ở Hình 31.
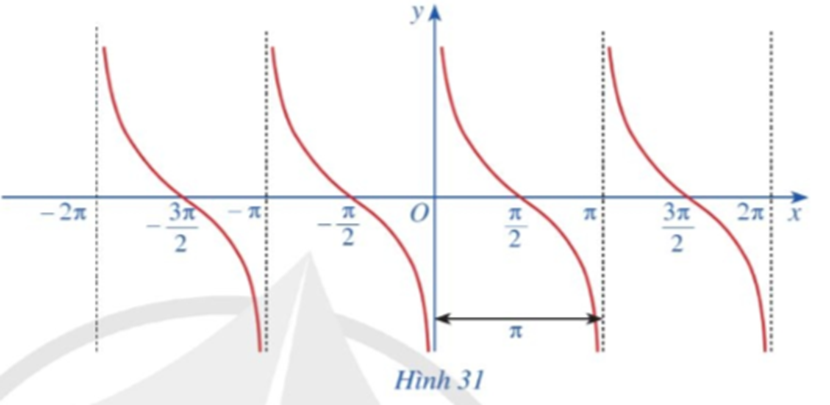
Tìm khoảng đồng biến, nghịch biến của hàm số y = cotx.
Quan sát đồ thị hàm số y = cotx ở Hình 31.

Tìm khoảng đồng biến, nghịch biến của hàm số y = cotx.
Câu 2:
Quan sát đồ thị hàm số y = sinx ở Hình 24.
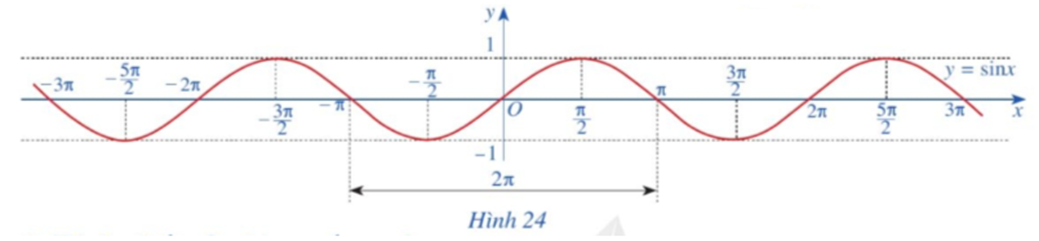
Tìm khoảng đồng biến, nghịch biến của hàm số y = sinx.
Quan sát đồ thị hàm số y = sinx ở Hình 24.

Tìm khoảng đồng biến, nghịch biến của hàm số y = sinx.
Câu 3:
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = sinx nhận giá trị bằng 1;
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = sinx nhận giá trị bằng 1;Câu 4:
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = cosx nhận giá trị bằng 0.
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn [‒2π; 2π] để:
Hàm số y = cosx nhận giá trị bằng 0.
Câu 6:
Dùng đồ thị hàm số, hãy cho biết:
Với mỗi m ∈ [‒1;1], có bao nhiêu giá trị α∈[−π2;π2] sao cho sinα = m;
Dùng đồ thị hàm số, hãy cho biết:
Với mỗi m ∈ [‒1;1], có bao nhiêu giá trị α∈[−π2;π2] sao cho sinα = m;
Câu 7:
Quan sát đồ thị hàm số y = cosx ở Hình 27.
![Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [-pi; pi] song song với trục (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid27-1689051716.png)
Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta nhận được đồ thị hàm số y = cosx trên đoạn [π; 3π] hay không? Hàm số y = cosx có tuần hoàn hay không?
Quan sát đồ thị hàm số y = cosx ở Hình 27.
![Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [-pi; pi] song song với trục (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid27-1689051716.png)
Bằng cách dịch chuyển đồ thị hàm số y = cosx trên đoạn [‒π; π] song song với trục hoành sang phải theo đoạn có độ dài 2π, ta nhận được đồ thị hàm số y = cosx trên đoạn [π; 3π] hay không? Hàm số y = cosx có tuần hoàn hay không?
Câu 8:
Dùng đồ thị hàm số, hãy cho biết:
Với mỗi m ∈ [‒1;1], có bao nhiêu giá trị α ∈ [0; π] sao cho cosα = m
Dùng đồ thị hàm số, hãy cho biết:
Câu 9:
Làm tương tự như trên đối với các khoảng (π2;3π2),(−3π2;−π2), …, ta có đồ thị hàm số y = tan x trên D được biểu diễn ở Hình 29.
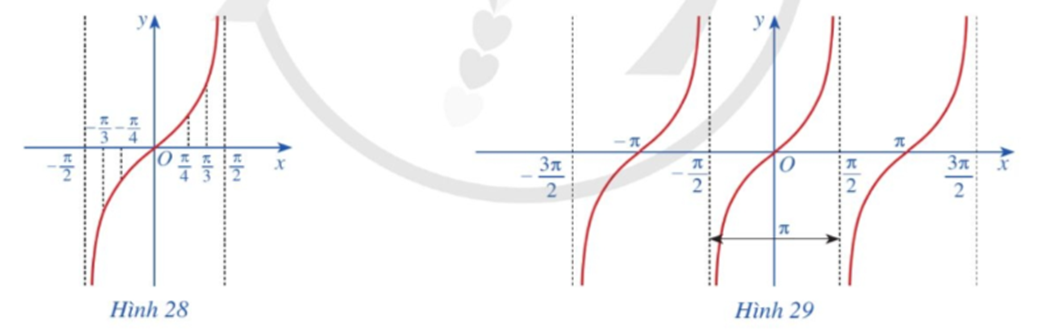
Câu 10:
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng (−π;3π2) để:
Hàm số y = cotx nhận giá trị bằng 0.
Dùng đồ thị hàm số, tìm giá trị của x trên khoảng (−π;3π2) để:
Hàm số y = cotx nhận giá trị bằng 0.Câu 12:
Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = tanx trên khoảng (−π2;π2).
Với mỗi số thực m, tìm số giao điểm của đường thẳng y = m và đồ thị hàm số y = tanx trên khoảng (−π2;π2).
Câu 13:
Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], ta có đồ thị hàm số y = cosx trên ℝ được biểu diễn ở Hình 27.
![Làm tương tự như trên đối với các đoạn [-3pi; -pi], [pi; 3pi], ta có đồ thị hàm số y (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid23-1689051624.png)
Làm tương tự như trên đối với các đoạn [‒3π; ‒π], [π; 3π], ta có đồ thị hàm số y = cosx trên ℝ được biểu diễn ở Hình 27.
![Làm tương tự như trên đối với các đoạn [-3pi; -pi], [pi; 3pi], ta có đồ thị hàm số y (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/07/blobid23-1689051624.png)
Câu 14:
Dùng đồ thị hàm số, hãy cho biết:
Với mỗi m ∈ ℝ, có bao nhiêu giá trị α∈(−π2;π2) sao cho tanα = m;
Dùng đồ thị hàm số, hãy cho biết:
Với mỗi m ∈ ℝ, có bao nhiêu giá trị α∈(−π2;π2) sao cho tanα = m;
Câu 15:
Quan sát đồ thị hàm số y = tanx ở Hình 29.

Tìm khoảng đồng biến, nghịch biến của hàm số y = tanx.
Quan sát đồ thị hàm số y = tanx ở Hình 29.

Tìm khoảng đồng biến, nghịch biến của hàm số y = tanx.


