Câu hỏi:
16/07/2024 93
Chứng minh rằng phương trình x5 + 3x2 ‒ 1 = 0 trong mỗi khoảng (‒2; ‒1), (‒1; 0) và (0; 1) đều có ít nhất một nghiệm.
Chứng minh rằng phương trình x5 + 3x2 ‒ 1 = 0 trong mỗi khoảng (‒2; ‒1), (‒1; 0) và (0; 1) đều có ít nhất một nghiệm.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Xét hàm số f(x) = x5 + 3x2 ‒ 1. Hàm số này liên tục trên ℝ.
Ta có:
f(‒2) = (‒2)5 + 3.(‒2)2 ‒ 1 = ‒32 + 12 ‒ 1 = ‒21.
f(‒1) = (‒1)5 + 3.(‒1)2 ‒ 1 = ‒1 + 3 ‒ 1 = 1.
f(0) = 05 + 3.02 ‒ 1 = ‒1.
f(1) = 15 + 3.12 ‒ 1 = 3.
Do f(‒2).f(‒1) = ‒21 < 0 nên phương trình f(x) có nghiệm thuộc (‒2; ‒1).
Do f(‒1).f(0) < 0 nên phương trình f(x) = 0 có nghiệm thuộc (‒1; 0).
Do f(0).f(1) = ‒3 < 0 nên phương trình f(x) = 0 có nghiệm thuộc (0; 1).
Vậy trong mỗi khoảng (‒2; ‒1), (‒1; 0) và (0; 1) phương trình f(x) = 0 hay x5 + 3x2 ‒ 1 = 0 đều có ít nhất một nghiệm.
Xét hàm số f(x) = x5 + 3x2 ‒ 1. Hàm số này liên tục trên ℝ.
Ta có:
f(‒2) = (‒2)5 + 3.(‒2)2 ‒ 1 = ‒32 + 12 ‒ 1 = ‒21.
f(‒1) = (‒1)5 + 3.(‒1)2 ‒ 1 = ‒1 + 3 ‒ 1 = 1.
f(0) = 05 + 3.02 ‒ 1 = ‒1.
f(1) = 15 + 3.12 ‒ 1 = 3.
Do f(‒2).f(‒1) = ‒21 < 0 nên phương trình f(x) có nghiệm thuộc (‒2; ‒1).
Do f(‒1).f(0) < 0 nên phương trình f(x) = 0 có nghiệm thuộc (‒1; 0).
Do f(0).f(1) = ‒3 < 0 nên phương trình f(x) = 0 có nghiệm thuộc (0; 1).
Vậy trong mỗi khoảng (‒2; ‒1), (‒1; 0) và (0; 1) phương trình f(x) = 0 hay x5 + 3x2 ‒ 1 = 0 đều có ít nhất một nghiệm.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho hàm số f(x)=x2−3x|x−3|. Đặt a=limx→3+f(x) và b=limx→3−f(x). Giá trị của a ‒ 2b bằng
A. 0.
B. 9.
C. ‒3.
D. ‒9.
Cho hàm số f(x)=x2−3x|x−3|. Đặt a=limx→3+f(x) và b=limx→3−f(x). Giá trị của a ‒ 2b bằng
A. 0.
B. 9.
C. ‒3.
D. ‒9.
Câu 3:
Biết rằng limx→+∞2ax√x2+ax+x=3. Giá trị của a là
A. 34
B. 6.
C. 32
D. 3.
Biết rằng limx→+∞2ax√x2+ax+x=3. Giá trị của a là
A. 34
B. 6.
C. 32
D. 3.
Câu 4:
Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau:
Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích 14 ).
Bước 2: Làm tương tự như Bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác, mỗi tam giác có diện tích 142 ).
Cứ tiếp tục quá trình như vậy (ở bước thứ n, bỏ đi 3n‒1 tam giác, mỗi tam giác diện tích 14n ). Tính tổng diện tích các tam giác đã bỏ đi.

Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau:
Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích 14 ).
Bước 2: Làm tương tự như Bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác, mỗi tam giác có diện tích 142 ).
Cứ tiếp tục quá trình như vậy (ở bước thứ n, bỏ đi 3n‒1 tam giác, mỗi tam giác diện tích 14n ). Tính tổng diện tích các tam giác đã bỏ đi.

Câu 5:
Biết rằng, từ vị trí A, một mũi tên bay với tốc độ 10 m/s hướng thẳng tới bia mục tiêu đặt ở vị trí B cách vị trí A một khoảng bằng 10 m (Hình 2). Một nhà thông thái lập luận như sau: “Để đến được B, trước hết mũi tên phải đến trung điểm A1 của AB. Tiếp theo, nó phải đến trung điểm A2 của A1B. Tiếp nữa, nó phải đến trung điểm A3 của A2B. Cứ tiếp tục như vậy, vì không bao giờ hết các trung điểm nên mũi tên không thể bay đến được bia mục tiêu ở B”.
Lập luận trên có đúng không? Nếu không, hãy chỉ ra chỗ sai lầm.

Biết rằng, từ vị trí A, một mũi tên bay với tốc độ 10 m/s hướng thẳng tới bia mục tiêu đặt ở vị trí B cách vị trí A một khoảng bằng 10 m (Hình 2). Một nhà thông thái lập luận như sau: “Để đến được B, trước hết mũi tên phải đến trung điểm A1 của AB. Tiếp theo, nó phải đến trung điểm A2 của A1B. Tiếp nữa, nó phải đến trung điểm A3 của A2B. Cứ tiếp tục như vậy, vì không bao giờ hết các trung điểm nên mũi tên không thể bay đến được bia mục tiêu ở B”.
Lập luận trên có đúng không? Nếu không, hãy chỉ ra chỗ sai lầm.

Câu 6:
Cho hàm số f(x)={x2−9|x+3| khi x≠−3a khi x=−3.
a) Tìm limx→−3+f(x)−limx→−3−f(x).
b) Với giá trị nào của a thì hàm số liên tục tại x = ‒3?
Cho hàm số f(x)={x2−9|x+3| khi x≠−3a khi x=−3.
a) Tìm limx→−3+f(x)−limx→−3−f(x).
b) Với giá trị nào của a thì hàm số liên tục tại x = ‒3?
Câu 7:
Biết limx→1x2−3x+ax−1=b với a và b là hai số thực. Giá trị của a + b bằng
A. 1.
B. 2.
C. 4.
D. 5.
Biết limx→1x2−3x+ax−1=b với a và b là hai số thực. Giá trị của a + b bằng
A. 1.
B. 2.
C. 4.
D. 5.
Câu 8:
Biết rằng phương trình x3 ‒ 2x ‒ 3 = 0 chỉ có một nghiệm. Phương trình này có nghiệm trong khoảng nào sau đây?
A. (‒1; 0).
B. (0; 1).
C. (1; 2).
D. (2; 3).
Biết rằng phương trình x3 ‒ 2x ‒ 3 = 0 chỉ có một nghiệm. Phương trình này có nghiệm trong khoảng nào sau đây?
A. (‒1; 0).
B. (0; 1).
C. (1; 2).
D. (2; 3).
Câu 9:
Cho hai dãy số (un) và (vn) thoả mãn limun = 4, lim(vn – 3) = 0.
lim[un(un – vn)] bằng
A. 7.
B. 12.
C. 4.
D. 28.
Cho hai dãy số (un) và (vn) thoả mãn limun = 4, lim(vn – 3) = 0.
lim[un(un – vn)] bằng
A. 7.
B. 12.
C. 4.
D. 28.
Câu 10:
Cho các dãy số (un) và (vn) thoả mãn limun = 2, lim(un – vn) = 4. Tìm lim3un−vnunvn+3.
Cho các dãy số (un) và (vn) thoả mãn limun = 2, lim(un – vn) = 4. Tìm lim3un−vnunvn+3.
Câu 11:
Cho điểm M thay đổi trên parabol y = x2; H là hình chiếu vuông góc của M trên trục hoành. Gọi x là hoành độ của điểm H.
Tìm limx→+∞(OM−MH).
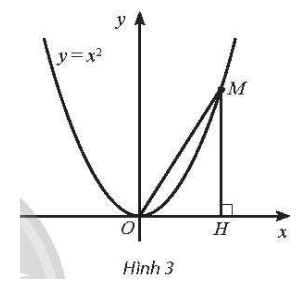
Cho điểm M thay đổi trên parabol y = x2; H là hình chiếu vuông góc của M trên trục hoành. Gọi x là hoành độ của điểm H.
Tìm limx→+∞(OM−MH).

Câu 12:
Cho hàm số f(x)={tanxkhi 0≤x≤π4k−cotx khi π4<x≤π2 liên tục trên đoạn [0;π2].Giá trị của k bằng:
A. 0.
B. 1.
C. 2.
D. π2
Cho hàm số f(x)={tanxkhi 0≤x≤π4k−cotx khi π4<x≤π2 liên tục trên đoạn [0;π2].Giá trị của k bằng:
A. 0.
B. 1.
C. 2.
D. π2
Câu 13:
Tại một bể bơi có dạng hình tròn có đường kính AB = 10 m, một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc α(0<α<π2), rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi S(α) là quãng đường người đó đã di chuyển.
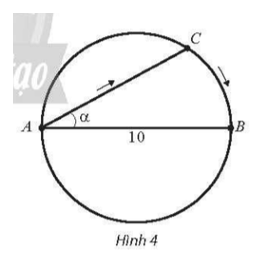
a) Viết công thức tính S(α) theo α(0<α<π2) .
b) Xét tính liên tục của hàm số y = S(α) trên khoảng (0;π2) .
c) Tính các giới hạn limx→0+S(α) và limx→π2+S(α).
Tại một bể bơi có dạng hình tròn có đường kính AB = 10 m, một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc α(0<α<π2), rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi S(α) là quãng đường người đó đã di chuyển.

a) Viết công thức tính S(α) theo α(0<α<π2) .
b) Xét tính liên tục của hàm số y = S(α) trên khoảng (0;π2) .
c) Tính các giới hạn limx→0+S(α) và limx→π2+S(α).
Câu 14:
Biết rằng hàm số f(x)={2−√x+1x−3 khi x≠3a khi x=3 liên tục tại điểm x = 3. Giá trị của a bằng
A. -14
B. 14
C. ‒2.
D. 3.
Biết rằng hàm số f(x)={2−√x+1x−3 khi x≠3a khi x=3 liên tục tại điểm x = 3. Giá trị của a bằng
A. -14
B. 14
C. ‒2.
D. 3.


