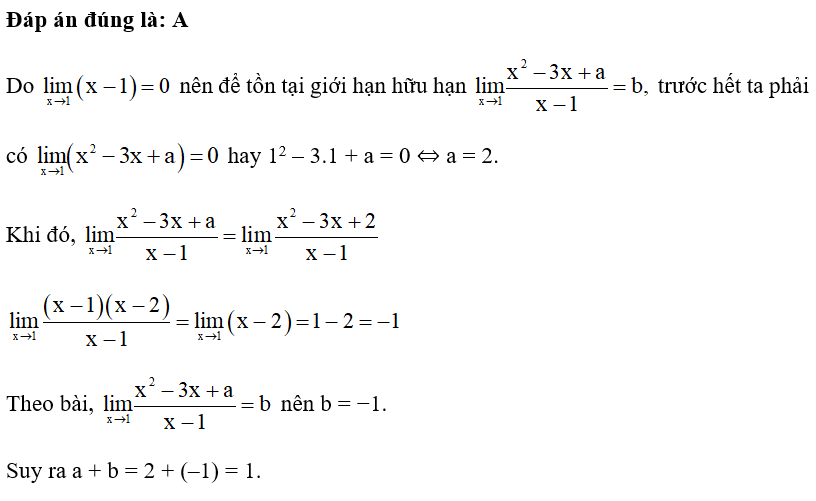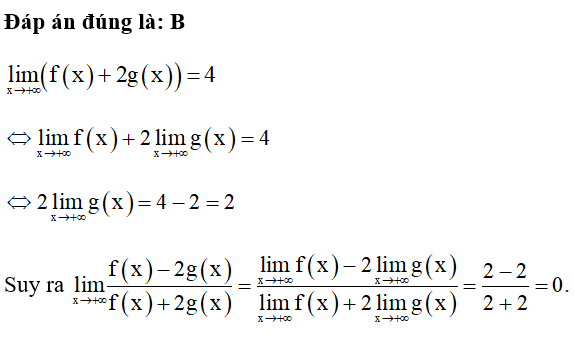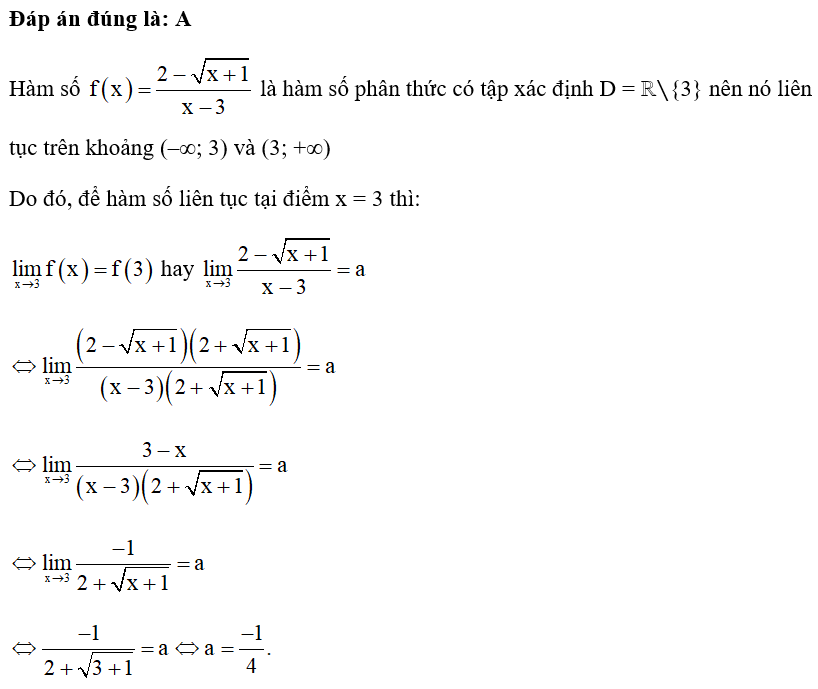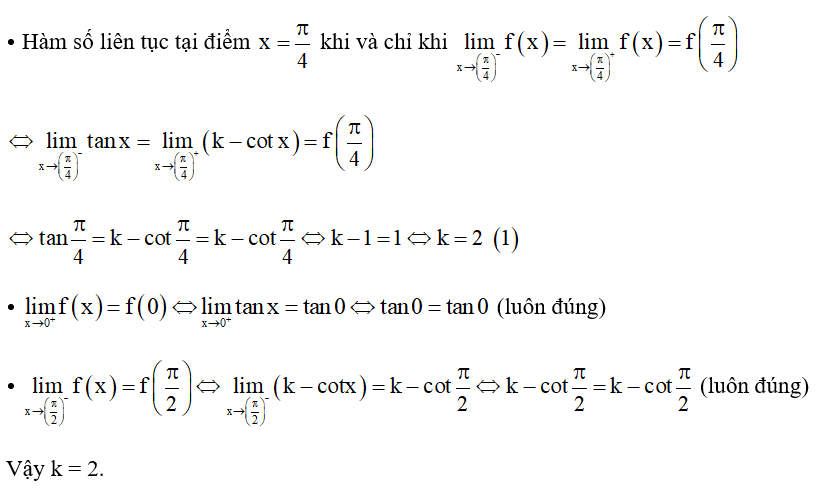27 câu hỏi trắc nghiệm thuộc Giải SBT Toán 11 CTST Bài tập cuối chương 3

Câu 1:

17/06/2026

$lim \frac{3 n^{2} + 2 n}{2 - n^{2}}$ bằng

A. $\frac{3}{2}$

B. ‒2.

C. 3.

D. ‒3.

Xem đáp án

Đáp án đúng là: D

Ta có: $lim \frac{3 n^{2} + 2 n}{2 - n^{2}} = \lim \frac{3 + \frac{2}{n}}{\frac{2}{n^{2}} - 1} = \frac{3}{- 1} = - 3.$

Câu 2:

17/06/2026

$lim \frac{\sqrt{4 n^{2} + 4 n + 1}}{4 n + 1}$ bằng

A. $\frac{1}{2}$

B. 1.

C. 2.

D. +∞.

Xem đáp án

Đáp án đúng là: A

$lim \frac{\sqrt{4 n^{2} + 4 n + 1}}{4 n + 1} = \lim \frac{\sqrt{4 + \frac{4}{n} + \frac{1}{n^{2}}}}{4 + \frac{1}{n}} = \frac{\sqrt{4}}{4} = \frac{1}{2} .$

Câu 3:

17/06/2026

$lim \frac{2 n + 1}{\sqrt{9 n^{2} + 1} - n}$ bằng

A. $\frac{2}{3}$

B. 1.

C. $\frac{1}{4}$

D. 2.

Xem đáp án

Đáp án đúng là: B

$lim \frac{2 n + 1}{\sqrt{9 n^{2} + 1} - n} = \lim \frac{2 + \frac{1}{n}}{\sqrt{9 + \frac{1}{n^{2}}} - 1} = \frac{2}{3 - 1} = 1.$

Câu 4:

17/06/2026

Cho hai dãy số (u_n) và (v_n) thoả mãn limu_n = 4, lim(v_n – 3) = 0.

lim[u_n(u_n – v_n)] bằng

A. 7.

B. 12.

C. 4.

D. 28.

Xem đáp án

Đáp án đúng là: C

Ta có lim(v_n ‒ 3) = 0 ⇔ limv_n = 3

Khi đó $lim [u_{n} (u_{n} - v_{n})] = \lim (u_{n}^{2} - u_{n} v_{n}) = 4^{2} - (4 \cdot 3) = 4.$

Câu 5:

17/06/2026

$lim \frac{4^{n}}{2 \cdot 4^{n} + 3^{n}}$ bằng

A. $\frac{1}{2}$

B. 1.

C. 4.

D. 0.

Xem đáp án

Đáp án đúng là: A

Ta có: $lim \frac{4^{n}}{2 \cdot 4^{n} + 3^{n}} = \lim \frac{1}{2 + {(\frac{3}{4})}^{n}} = \frac{1}{2} .$

Câu 6:

17/06/2026

$\lim_{x \to 2} \frac{x^{2} - x - 2}{2 x - 4}$ bằng

A. $\frac{3}{2}$

B. $\frac{1}{2}$

C. 1.

D. $\frac{- 1}{2}$

Xem đáp án

Đáp án đúng là: A

Ta có $\lim_{x \to 2} \frac{x + 1}{2} = \lim_{x \to 2} \frac{(x - 2) (x + 1)}{2 (x - 2)} = \lim_{x \to 2} \frac{x + 1}{2} = \frac{2 + 1}{2} = \frac{3}{2} .$

Câu 7:

17/06/2026

$\lim_{x \to 1} \frac{2 x - 2}{\sqrt{x + 3} - 2}$ bằng

A. 0.

B. +∞.

C. 2.

D. 8.

Xem đáp án

Đáp án đúng là: D

Ta có $\frac{2 x - 2}{\sqrt{x + 3} - 2} = \frac{(2 x - 2) (\sqrt{x + 3} + 2)}{(x + 3 - 4)}$ $= \frac{2 (x - 1) (\sqrt{x + 3} + 2)}{x - 1} = 2 (\sqrt{x + 3} + 2) .$

Khi đó $\lim_{x \to 1} \frac{2 x - 2}{\sqrt{x + 3} - 2} = \lim_{x \to 1} [2 (\sqrt{x + 3} + 2)] = 2 \cdot (\sqrt{1 + 3} + 2) = 8.$

Câu 8:

17/06/2026

Biết $\lim_{x \to 1} \frac{x^{2} - 3 x + a}{x - 1} = b$ với a và b là hai số thực. Giá trị của a + b bằng

A. 1.

B. 2.

C. 4.

D. 5.

Xem đáp án

Biết lim x^2 - 3x +a/ x -1= b với a và b là hai số thực. Giá trị của a + b bằng A. 1. B. 2. C. 4. D. 5. (ảnh 1)

Câu 9:

17/06/2026

Cho hàm số $f (x) = \frac{x^{2} - 3 x}{|x - 3|} .$ Đặt $a = \lim_{x \to 3^{+}} f (x)$ và $b = \lim_{x \to 3^{-}} f (x) .$ Giá trị của a ‒ 2b bằng

A. 0.

B. 9.

C. ‒3.

D. ‒9.

Xem đáp án

Đáp án đúng là: B

Ta có: $a = \lim_{x \to 3^{+}} f (x) = \lim_{x \to 3^{+}} \frac{x^{2} - 3 x}{|x - 3|} = \lim_{x \to 3^{+}} \frac{x^{2} - 3 x}{x - 3} = \lim_{x \to 3^{+}} x = 3.$ $b = \lim_{x \to 3^{-}} f (x) = \lim_{x \to 3^{-}} \frac{x^{2} - 3 x}{|x - 3|} = \lim_{x \to 3^{-}} \frac{x^{2} - 3 x}{3 - x} = \lim_{x \to 3^{-}} (- x) = - 3.$

Khi đó a ‒ 2b = 3 ‒ 2.(‒3) = 9.

Câu 10:

17/06/2026

Biết rằng $\lim_{x \to + \infty} f (x) = 2, \lim_{x \to + \infty} (f (x) + 2 g (x)) = 4$ . Giới hạn $\lim_{x \to + \infty} \frac{f (x) - 2 g (x)}{f (x) + 2 g (x)}$ bằng

A. ‒1.

B. 0.

C. $\frac{1}{2}$

D. $\frac{- 1}{2}$

Xem đáp án

Biết rằng lim f(x) = 2; lim( f(x) + 2g(x))= 4 . Giới hạn (ảnh 1)

Câu 11:

17/06/2026

Biết rằng $\lim_{x \to + \infty} \frac{2 a x}{\sqrt{x^{2} + a x} + x} = 3.$ Giá trị của a là

A. $\frac{3}{4}$

B. 6.

C. $\frac{3}{2}$

D. 3.

Xem đáp án

Đáp án đúng là: D

Ta có $\lim_{x \to + \infty} \frac{2 a x}{\sqrt{x^{2} + a x} + x} = 3 \Leftrightarrow \lim_{x \to + \infty} \frac{2 a}{\sqrt{1 + \frac{a}{x}} + 1} = 3 \Leftrightarrow \frac{2 a}{2} = 3 \Leftrightarrow a = 3.$

Câu 12:

17/06/2026

$\lim_{x \to - 2^{-}} \frac{1 - 3 x}{x + 2}$ bằng

A. +∞.

B. ‒∞.

C. ‒3 .

D. $\frac{7}{4}$

Xem đáp án

Đáp án đúng là: B

Do $\lim_{x \to - 2^{-}} (1 - 3 x) = 1 - 3 \cdot (- 2) = 1 + 6 = 7; \lim_{x \to - 2^{-}} \frac{1}{x + 2} = - \infty$

Nên $\lim_{x \to - 2^{-}} \frac{1 - 3 x}{x + 2} = \lim_{x \to - 2^{-}} [(1 - 3 x) \cdot \frac{1}{x + 2}] = - \infty .$

Câu 13:

17/06/2026

Biết rằng hàm số $f (x) = \{\begin{matrix} \frac{2 - \sqrt{x + 1}}{x - 3} & khi x \neq 3 \\ a & khi x = 3 \end{matrix}$ liên tục tại điểm x = 3. Giá trị của a bằng

A. $\frac{- 1}{4}$

B. $\frac{1}{4}$

C. ‒2.

D. 3.

Xem đáp án

Biết rằng hàm số f(x)= 2- căn x+1 khi x khác 3; a khi x = 3 liên tục tại điểm x = 3. Giá trị của a bằng (ảnh 1)

Câu 14:

17/06/2026

Cho hàm số $f (x) = \{\begin{matrix} tan x & khi 0 \leq x \leq \frac{π}{4} \\ k - cot x & khi \frac{π}{4} < x \leq \frac{π}{2} \end{matrix}$ liên tục trên đoạn $[0; \frac{π}{2}] .$ Giá trị của k bằng:

A. 0.

B. 1.

C. 2.

D. $\frac{π}{2}$

Xem đáp án

Cho hàm số f(x) = tan x khi 0 khi 0 nhỏ hơn hoặc bằng x nhỏ hơn hoặc bằng pi/4; k- cot x khi pi/4 nhỏ hơn x nhỏ hơn hoặc bằng pi/2 (ảnh 2)

Câu 15:

17/06/2026

Biết rằng phương trình x³ ‒ 2x ‒ 3 = 0 chỉ có một nghiệm. Phương trình này có nghiệm trong khoảng nào sau đây?

A. (‒1; 0).

B. (0; 1).

C. (1; 2).

D. (2; 3).

Xem đáp án

Đáp án đúng là: C

Xét hàm số f(x) = x³ ‒ 2x ‒3 liên tục trên ℝ.

f(‒1) = (‒1)³ ‒ 2.(‒1) ‒ 3 = ‒2.

f(0) = 0³ ‒ 2.0 ‒ 3 = ‒ 3.

f(1) = 1³ ‒ 2.1 ‒ 3 = ‒4.

f(2) = 2³ ‒ 2.2 ‒ 3 = 1.

f(3) = 3³ ‒ 2.3 ‒ 3 = 18.

Ta thấy f(1).f(2) < 0 nên hàm số có nghiệm trong các khoảng (1; 2).

Câu 16:

17/06/2026

Tìm các giới hạn sau:

a) $lim \frac{n (2 n^{2} + 3)}{4 n^{3} + 1}$ ; b) $lim [\sqrt{n} (\sqrt{n + 5} - \sqrt{n + 1})]$ .

Xem đáp án

Câu 17:

17/06/2026

Cho các dãy số (u_n) và (v_n) thoả mãn limu_n = 2, lim(u_n– v_n) = 4. Tìm $lim \frac{3 u_{n} - v_{n}}{u_{n} v_{n} + 3} .$

Xem đáp án

Ta có lim(u_n– v_n) = 4

Suy ra limu_n – limv_n = 4, hay limv_n = limu_n – 4 = 2 – 4 = −2.

Do đó $lim \frac{3 u_{n} - v_{n}}{u_{n} v_{n} + 3} = \frac{3 lim u_{n} - lim v_{n}}{lim u_{n} \cdot lim v_{n} + 3} = \frac{3 \cdot 2 - (- 2)}{2 \cdot (- 2) + 3} = - 8.$

Câu 18:

17/06/2026

Tìm $lim \frac{6^{n} + 4^{n}}{(2^{n} + 1) (3^{n} + 1)}$ .

Xem đáp án

Ta có $\frac{6^{n} + 4^{n}}{(2^{n} + 1) (3^{n} + 1)} = \frac{1 + {(\frac{2}{3})}^{n}}{(1 + \frac{1}{2^{n}}) (1 + \frac{1}{3^{n}})}$ (chia cả tử và mẫu cho 6ⁿ = 2ⁿ.3ⁿ).

Do đó $lim \frac{6^{n} + 4^{n}}{(2^{n} + 1) (3^{n} + 1)} = \lim \frac{1 + {(\frac{2}{3})}^{n}}{(1 + \frac{1}{2^{n}}) (1 + \frac{1}{3^{n}})} = \frac{1}{1 \cdot 1} = 1.$

Câu 19:

17/06/2026

Cho a > b > 0 và

lim \frac{a^{n + 1} + b^{n}}{2 a^{n} + b^{n + 1}} = 1.

Tìm giá trị của a

Xem đáp án

Cho a > b > 0 và lim a^ n +1 +b^n / 2. a^n + b^ n +1 = 1. Tìm giá trị của a (ảnh 1)

Câu 20:

17/06/2026

Cho dãy số (u_n) thoả mãn $\lim n u_{n} = \frac{1}{2} .$ Tìm lim(3n – 4)u_n.

Xem đáp án

Ta có $lim u_{n} = lim (\frac{1}{n} \cdot n u_{n}) = lim \frac{1}{n} \cdot lim n u_{n} = 0 \cdot \frac{1}{2} = 0$ .

Từ đó, $lim (3 n - 4) u_{n} = lim (3 n u_{n} - 4 u_{n}) = 3 \lim n u_{n} - 4 lim u_{n} = 3 \cdot \frac{1}{2} - 4 \cdot 0 = \frac{3}{2}$ .

Câu 21:

17/06/2026

Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau:

Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích $\frac{1}{4}$ ).

Bước 2: Làm tương tự như Bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác, mỗi tam giác có diện tích $\frac{1}{4^{2}}$ ).

Cứ tiếp tục quá trình như vậy (ở bước thứ n, bỏ đi 3^n‒1 tam giác, mỗi tam giác diện tích $\frac{1}{4^{n}}$ ). Tính tổng diện tích các tam giác đã bỏ đi.

Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau: Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích ). Bước 2: Làm tương tự như Bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác, mỗi tam giác có diện tích ). Cứ tiếp tục quá trình như vậy (ở bước thứ n, bỏ đi 3n‒1 tam giác, mỗi tam giác diện tích ). Tính tổng diện tích các tam giác đã bỏ đi. (ảnh 1)

Xem đáp án

Câu 22:

17/06/2026

Biết rằng, từ vị trí A, một mũi tên bay với tốc độ 10 m/s hướng thẳng tới bia mục tiêu đặt ở vị trí B cách vị trí A một khoảng bằng 10 m (Hình 2). Một nhà thông thái lập luận như sau: “Để đến được B, trước hết mũi tên phải đến trung điểm A₁ của AB. Tiếp theo, nó phải đến trung điểm A₂ của A₁B. Tiếp nữa, nó phải đến trung điểm A₃ của A₂B. Cứ tiếp tục như vậy, vì không bao giờ hết các trung điểm nên mũi tên không thể bay đến được bia mục tiêu ở B”.

Lập luận trên có đúng không? Nếu không, hãy chỉ ra chỗ sai lầm.

Xem đáp án

Câu 23:

17/06/2026

Cho hàm số $f (x) = \{\begin{matrix} \frac{x^{2} - 9}{|x + 3|} & khi x \neq - 3 \\ a & khi x = - 3. \end{matrix}$

a) Tìm $\lim_{x \to - 3^{+}} f (x) - \lim_{x \to - 3^{-}} f (x) .$

b) Với giá trị nào của a thì hàm số liên tục tại x = ‒3?

Xem đáp án

Cho hàm số f(x)= x^2 -9/ trị x+3 khi x khác -3; a khi x = -3 a) Tìm (ảnh 1)

Câu 24:

17/06/2026

Cho hàm số $f (x) = \frac{2 x + 1}{x - 3}$ .

a) Xét tính liên tục của hàm số đã cho.

b) Tìm các giới hạn $\lim_{x \to + \infty} f (x); \lim_{x \to - \infty} f (x); \lim_{x \to 3^{+}} f (x); \lim_{x \to 3} f (x) .$

Xem đáp án

Cho hàm số f(x)= 2x +1/ x - 3 . a) Xét tính liên tục của hàm số đã cho. b) Tìm các giới hạn (ảnh 1)

Câu 25:

17/06/2026

Cho điểm M thay đổi trên parabol y = x²; H là hình chiếu vuông góc của M trên trục hoành. Gọi x là hoành độ của điểm H.

Tìm $\lim_{x \to + \infty} (O M - M H) .$

Cho điểm M thay đổi trên parabol y = x^2; H là hình chiếu vuông góc của M trên trục hoành. Gọi x là hoành độ của điểm H. Tìm (ảnh 1)

Xem đáp án

Cho điểm M thay đổi trên parabol y = x^2; H là hình chiếu vuông góc của M trên trục hoành. Gọi x là hoành độ của điểm H. Tìm (ảnh 2)

Câu 26:

17/06/2026

Chứng minh rằng phương trình x⁵ + 3x² ‒ 1 = 0 trong mỗi khoảng (‒2; ‒1), (‒1; 0) và (0; 1) đều có ít nhất một nghiệm.

Xem đáp án

Xét hàm số f(x) = x⁵ + 3x² ‒ 1. Hàm số này liên tục trên ℝ.

Ta có:

f(‒2) = (‒2)⁵ + 3.(‒2)² ‒ 1 = ‒32 + 12 ‒ 1 = ‒21.

f(‒1) = (‒1)⁵ + 3.(‒1)² ‒ 1 = ‒1 + 3 ‒ 1 = 1.

f(0) = 0⁵ + 3.0² ‒ 1 = ‒1.

f(1) = 1⁵ + 3.1² ‒ 1 = 3.

Do f(‒2).f(‒1) = ‒21 < 0 nên phương trình f(x) có nghiệm thuộc (‒2; ‒1).

Do f(‒1).f(0) < 0 nên phương trình f(x) = 0 có nghiệm thuộc (‒1; 0).

Do f(0).f(1) = ‒3 < 0 nên phương trình f(x) = 0 có nghiệm thuộc (0; 1).

Vậy trong mỗi khoảng (‒2; ‒1), (‒1; 0) và (0; 1) phương trình f(x) = 0 hay x⁵ + 3x² ‒ 1 = 0 đều có ít nhất một nghiệm.

Câu 27:

17/06/2026

Tại một bể bơi có dạng hình tròn có đường kính AB = 10 m, một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc $α (0 < α < \frac{π}{2}),$ rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi S(α) là quãng đường người đó đã di chuyển.

Tại một bể bơi có dạng hình tròn có đường kính AB = 10 m, một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi S(α) là quãng đường người đó đã di chuyển. (ảnh 1)

a) Viết công thức tính S(α) theo $α (0 < α < \frac{π}{2})$ .

b) Xét tính liên tục của hàm số y = S(α) trên khoảng $(0; \frac{π}{2})$ .

c) Tính các giới hạn $\lim_{x \to 0^{+}} S (α)$ và $\lim_{x \to {\frac{π}{2}}^{+}} S (α) .$

Xem đáp án

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3