Câu hỏi:
17/07/2024 178
Cho tứ diện đều ABCD. Chứng minh rằng AB ⊥ CD.
Cho tứ diện đều ABCD. Chứng minh rằng AB ⊥ CD.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
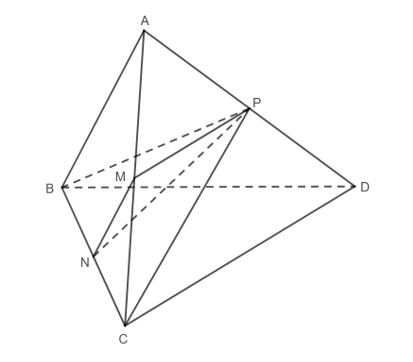
Gọi a là độ dài cạnh của tứ diện đều ABCD.
Gọi M, N, P lần lượt là trung điểm của các cạnh AC, BC và AD.
Xét tam giác ABC:
M là trung điểm của AC.
N là trung điểm của BC.
Nên MN là đường trung bình của tam giác ABC.
⇒ MN // AB; MN = 12 AB = a2 (1)
Tương tự: MP là đường trung bình tam giác ACD:
⇒ MP // CD; MP = 12 CD = a2 (2)
Từ (1) và (2) ⇒MN = MP = a2
Tam giác ABD đều có BP là trung tuyến nên BP = a√32
Tam giác ACD đều có CP là trung tuyến nên CP = a√32
Xét tam giác BCP có: BP = CP = a√32
⇒ Tam giác BCP cân tại P.
Mà N là trung điểm của BC ⇒ PN là đường trung tuyến nên PN ⊥ CN
PN = √CP2−CN2=√(a√32)2−(a2)2=a√22
Xét tam giác MNP:
MP2 + MN2 = ; PN2 =
MP2 + MN2 = PN2
Tam giác MNP vuông tại M.
Ta có: (AB, CD) = (MN, MP) = .
Vậy AB ⊥ CD.

Gọi a là độ dài cạnh của tứ diện đều ABCD.
Gọi M, N, P lần lượt là trung điểm của các cạnh AC, BC và AD.
Xét tam giác ABC:
M là trung điểm của AC.
N là trung điểm của BC.
Nên MN là đường trung bình của tam giác ABC.
⇒ MN // AB; MN = 12 AB = a2 (1)
Tương tự: MP là đường trung bình tam giác ACD:
⇒ MP // CD; MP = 12 CD = a2 (2)
Từ (1) và (2) ⇒MN = MP = a2
Tam giác ABD đều có BP là trung tuyến nên BP = a√32
Tam giác ACD đều có CP là trung tuyến nên CP = a√32
Xét tam giác BCP có: BP = CP = a√32
⇒ Tam giác BCP cân tại P.
Mà N là trung điểm của BC ⇒ PN là đường trung tuyến nên PN ⊥ CN
PN = √CP2−CN2=√(a√32)2−(a2)2=a√22
Xét tam giác MNP:
MP2 + MN2 = ; PN2 =
MP2 + MN2 = PN2
Tam giác MNP vuông tại M.
Ta có: (AB, CD) = (MN, MP) = .
Vậy AB ⊥ CD.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:
a) AB và BB′;
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:
a) AB và BB′;
Câu 2:
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông M, N, E, F lần lượt là trung điểm các cạnh BC, BA, AA′, A′D′. Tính góc giữa các cặp đường thẳng:
a) MN và DD′;
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông M, N, E, F lần lượt là trung điểm các cạnh BC, BA, AA′, A′D′. Tính góc giữa các cặp đường thẳng:
a) MN và DD′;
Câu 3:
Cho hình chóp S.ABC có SA = SB = SC = a, Cho I và J lần lượt là trung điểm của SA và BC. Chứng minh rằng IJ ⊥ SA và IJ ⊥ BC.
Cho hình chóp S.ABC có SA = SB = SC = a, Cho I và J lần lượt là trung điểm của SA và BC. Chứng minh rằng IJ ⊥ SA và IJ ⊥ BC.
Câu 4:
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và AD. Biết AB = CD = 2a và MN = . Tính góc giữa AB và CD.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và AD. Biết AB = CD = 2a và MN = . Tính góc giữa AB và CD.
Câu 5:
Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm CD. Tính góc giữa hai đường thẳng AK và BC.
Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm CD. Tính góc giữa hai đường thẳng AK và BC.
Câu 6:
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông.
a) Tìm các đường thẳng đi qua hai đỉnh của hình lập phương và vuông góc với AC.
Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông.
a) Tìm các đường thẳng đi qua hai đỉnh của hình lập phương và vuông góc với AC.
Câu 7:
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a. Cho biết SA = , SA ⊥ AB và SA ⊥ AD. Tính góc giữa SB và CD, SD và CB.
Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a. Cho biết SA = , SA ⊥ AB và SA ⊥ AD. Tính góc giữa SB và CD, SD và CB.
Câu 8:
Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác OMN vuông cân tại O. Tính góc giữa hai thanh gỗ a và b.
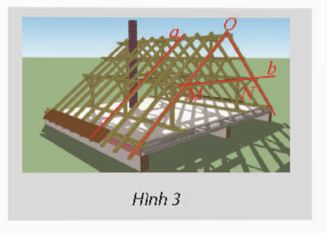
Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác OMN vuông cân tại O. Tính góc giữa hai thanh gỗ a và b.

Câu 9:
Một ô che nắng có viền khung hình lục giác đều ABCDEF song song với mặt bàn và có cạnh AB song song với cạnh bàn a (Hình 5). Tính số đo góc hợp bởi đường thẳng a lần lượt với các đường thẳng AF, AE và AD.
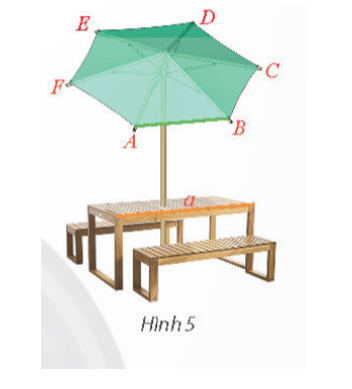
Một ô che nắng có viền khung hình lục giác đều ABCDEF song song với mặt bàn và có cạnh AB song song với cạnh bàn a (Hình 5). Tính số đo góc hợp bởi đường thẳng a lần lượt với các đường thẳng AF, AE và AD.

Câu 11:
Cho hai đường thẳng chéo nhau a và b trong không gian. Qua một điểm M tuỳ ý vẽ a // a′ và vẽ b // b′. Khi thay đổi vị trí của điểm M, có nhận xét gì về góc giữa a′ và b′?
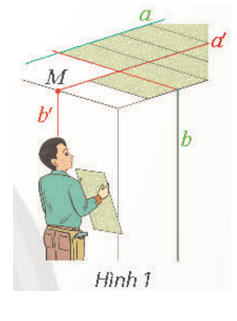
Cho hai đường thẳng chéo nhau a và b trong không gian. Qua một điểm M tuỳ ý vẽ a // a′ và vẽ b // b′. Khi thay đổi vị trí của điểm M, có nhận xét gì về góc giữa a′ và b′?

Câu 14:
b) Trong các đường thẳng tìm được ở câu a, tìm đường thẳng chéo với AC.
b) Trong các đường thẳng tìm được ở câu a, tìm đường thẳng chéo với AC.
Câu 15:
Ta đã biết cách xác định góc giữa hai đường thẳng cùng thuộc một mặt phẳng. Có góc giữa hai đường thẳng chéo nhau không? Nếu có, làm thế nào để xác định?
Ta đã biết cách xác định góc giữa hai đường thẳng cùng thuộc một mặt phẳng. Có góc giữa hai đường thẳng chéo nhau không? Nếu có, làm thế nào để xác định?



