Câu hỏi:
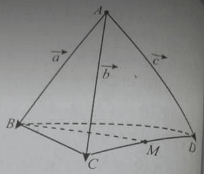
18/07/2024 207Cho tứ diện ABCD và đặt . Gọi M là trung điểm của CD.
Vecto bằng:
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ba vecto . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng?
Câu 2:
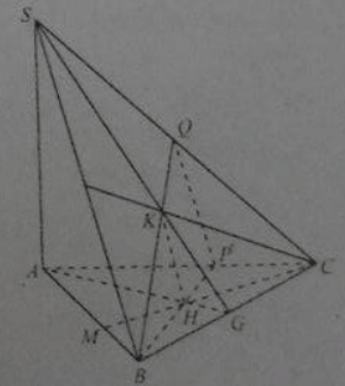
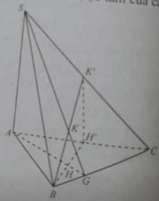
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Mặt phẳng (BKH) vuông góc với mặt phẳng:
Câu 4:
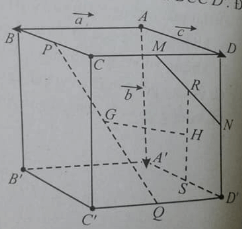
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt .
Đường thẳng GG’ song song với mặt phẳng (AA’B’B) vì:
Câu 5:
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC:
Đường thẳng HK vuông góc với mặt phẳng:
Câu 7:
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt .
Vecto bằng:
Câu 9:
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC:
Mặt phẳng (BKH) vuông góc với đường thẳng:
Câu 10:
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Đường thẳng BH vuông góc với đường thẳng:
Câu 11:
Cho tứ diện ABCD và đặt . Gọi M là trung điểm của CD.
Vecto bằng:
Câu 12:
Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC.
Mặt phẳng (BKH) vuông góc với đường thẳng: