Câu hỏi:
21/07/2024 172Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.
Vecto cùng với hai vecto nào sau đây là ba vecto đồng phẳng?
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Cách 1:
Ta có: M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC
suy ra: MN// AC và (1)
Tương tự: QP là đường trung bình của tam giác ACD nên QP // AC và (2)
Từ (1) và (2) suy ra: tứ giác MNPQ là hình bình hành (có các cạnh đối song song và bằng nhau)
* Cách 2:
Tam giác ABC có MN là đường trung bình nên MN // AC và
Do đó, 3 vecto đồng phẳng
Đáp án C
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc và đều có độ dài là l. Gọi M là trung điểm của các cạnh AB. Góc giữa hai vecto và bằng:
Câu 2:
Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, BC, CD, và DA.
Vecto cùng với hai vecto nào sau đây là ba vecto không đồng phẳng?
Câu 3:
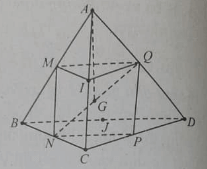
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
Những vecto khác bằng nhau là:
Câu 4:
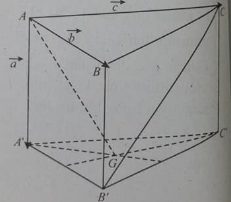
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt
Vecto bằng:
Câu 6:
Cho hình lăng trụ ABC.A’B’C’ với G là trọng tâm của tam giác A’B’C’. Đặt
Vecto bằng:
Câu 7:
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho và , với m khác 1. Vecto bằng:
Câu 8:
Cho tứ diện ABCD với G là trọng tâm và các điểm M, N, P, Q, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, AD, AC, BD.
bằng:
Câu 9:
Cho ba vecto . Điều kiện nào sau đây không kết luận được ba vecto đó đồng phẳng.