Câu hỏi:
23/07/2024 1,221
Cho tam giác ABC có ˆA=40o , ˆB − ˆC = 30°. Tính ˆB và ˆC .
Cho tam giác ABC có ˆA=40o , ˆB − ˆC = 30°. Tính ˆB và ˆC .
A. ˆB = 70°; ˆC = 40°;
B. ˆB = 65°; ˆC = 35°;
C. ˆB = 85°; ˆC = 55°;
D. ˆB = 75°; ˆC = 45°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Áp dụng định lý về tổng số đo ba góc của tam giác ta có:
ˆA + ˆB + ˆC = 180°
Suy ra ˆB= 180° − ˆA − ˆC = 180° − 40° − ˆC = 140° − ˆC
Ta có ˆB − ˆC = 30°
Suy ra 140° − ˆC − ˆC= 30°
Suy ra 140° − 2ˆC = 30°
Suy ra 2ˆC = 110°
Suy ra ˆC = 55°
Suy ra ˆB = 140° − ˆC = 85°
Vậy ˆB = 85°; ˆC = 55°.
Hướng dẫn giải
Đáp án đúng là: C
Áp dụng định lý về tổng số đo ba góc của tam giác ta có:
ˆA + ˆB + ˆC = 180°
Suy ra ˆB= 180° − ˆA − ˆC = 180° − 40° − ˆC = 140° − ˆC
Ta có ˆB − ˆC = 30°
Suy ra 140° − ˆC − ˆC= 30°
Suy ra 140° − 2ˆC = 30°
Suy ra 2ˆC = 110°
Suy ra ˆC = 55°
Suy ra ˆB = 140° − ˆC = 85°
Vậy ˆB = 85°; ˆC = 55°.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Cho tam giác ABC có AB = 2, BC = 8 cm. Biết độ dài cạnh AC là một số nguyên tố. Chu vi tam giác ABC là:
Cho tam giác ABC có AB = 2, BC = 8 cm. Biết độ dài cạnh AC là một số nguyên tố. Chu vi tam giác ABC là:
Câu 5:
Cho tam giác MNP có số đo như hình vẽ:
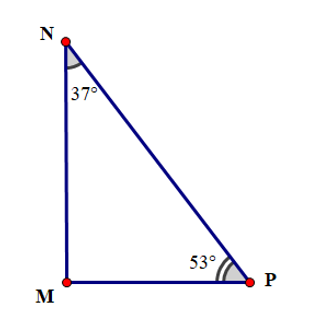
Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I). ˆM = 80°.
(II). Tam giác MNP là tam giác nhọn.
(III). Tam giác MNP là tam giác vuông.
(IV). NP là cạnh huyền của tam giác MNP.
Cho tam giác MNP có số đo như hình vẽ:

Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I). ˆM = 80°.
(II). Tam giác MNP là tam giác nhọn.
(III). Tam giác MNP là tam giác vuông.
(IV). NP là cạnh huyền của tam giác MNP.
Câu 6:
Điền vào chỗ trống:
“Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng … độ dài cạnh còn lại”
Điền vào chỗ trống:
“Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng … độ dài cạnh còn lại”
Câu 7:
Cho tam giác ABC có độ dài ba cạnh là ba số nguyên. Biết AB = 3 cm; AC = 7 cm. Khi đó độ dài cạnh BC không thể bằng
Cho tam giác ABC có độ dài ba cạnh là ba số nguyên. Biết AB = 3 cm; AC = 7 cm. Khi đó độ dài cạnh BC không thể bằng
Câu 8:
Cho tam giác MNP có ˆM = 2 ˆN = 13ˆP . Tia phân giác góc P cắt MN tại Q. Số đo ^MPQ là:
Cho tam giác MNP có ˆM = 2 ˆN = 13ˆP . Tia phân giác góc P cắt MN tại Q. Số đo ^MPQ là:
Câu 13:
Trong các bộ ba đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?
Trong các bộ ba đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?