Câu hỏi:
22/07/2024 216Cho hình thang cân ABCD (AB // CD); CD = 2AD = 2AB = 8. Tính diện tích của hình thang đó.
A.
B.
C. 12
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
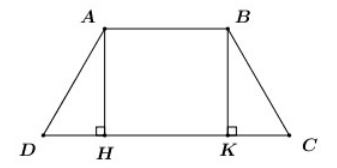
Kẻ AH, BK cùng cuông góc với CD (H, K CD)
Xét tứ giác ABKH có:, suy ra ABKH là hình bình hành.
Lại có nên ABKH là hình chữ nhật, do đó HK = AB = 4
AD = BC (tính chất hình thang cân)
= ACK (tính chất hình thang cân)
(cạnh huyền – góc nhọn)
=> DH = CK (hai cạnh tương ứng)
Mà DH + CK = CD – HK = 8 – 4 = 4
Do đó DH = CK = 2
Áp dụng định lý Py-ta-go trong tam giác vuông ADH ta có:
Vậy diện tích hình thang ABCD là:
Đáp án cần chọn là: B
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
Câu 2:
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 4,5cm
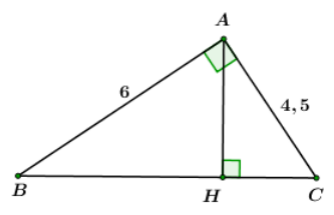
Tính các góc B, C và đường cao AH của tam giác?
Câu 3:
Cho ABC vuông tại A có đường cao AH và đường trung tuyến AM. Biết AH = 3cm; HB = 4cm. Hãy tính AB, AC, AM và diện tích tam giác ABC.
Câu 4:
Cho MNP vuông tại M có đường cao MH. Gọi I, K lần lượt là hình chiếu vuông góc của H trên MN, MP. Biết HK = 9cm, HI = 6cm. Khi đó tính độ dài các cạnh của MNP.
Câu 5:
Cho tam giác ABC có AB = 4cm, AC = , BC = 8cm.Tính số đo , và độ dài đường cao AH của ABC
Câu 6:
Cho tam giác ABC vuông tại A có AB = 21cm; , phân . Độ dài phân giác BD là? (kết quả làm tròn đến chữ số thập phân thứ nhất).
Câu 7:
Cạnh bên của tam giác ABC cân tại A dài 20cm, góc ở đáy là . Độ dài cạnh đáy của tam giác cân là? (kết quả làm tròn đến chữ số thập phân thứ nhất).
Câu 8:
Giải tam giác vuông ABC, biết và BC = 50cm; (làm tròn đến chữ số thập phân thứ nhất).
Câu 9:
Cho ABC vuông tại A, AB = 12cm, AC = 16cm, tia phân giác AD, đường cao AH. Tính HD.
Câu 12:
Cho tam giác ABC vuông tại A, và AB = 6cm. Vẽ đường cao AH và trung tuyến AM của tam giác ABC
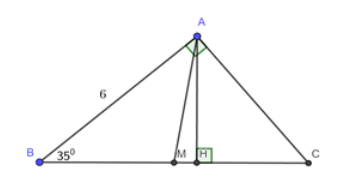
Giải tam giác ABC.
Câu 13:
Cho tam giác ABC vuông tại A, AB = 15cm; AC = 20cm. Phân giác của góc A cắt BC tại E.
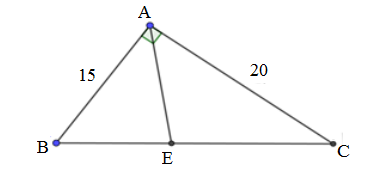
Giải tam giác ABC: