Câu hỏi:
11/10/2024 454
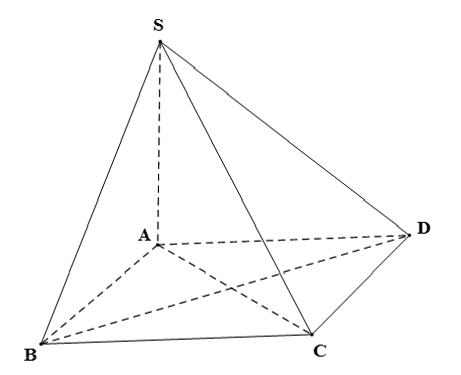
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA ⊥ (ABCD). Chứng minh rằng (SAC) ⊥ (SBD).
Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA ⊥ (ABCD). Chứng minh rằng (SAC) ⊥ (SBD).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
*Phương pháp giải:
* Chứng minh hai mặt phẳng vuông góc
Để chứng minh (P) ⊥ (Q), ta có thể chứng minh bởi một trong các cách sau:
- Chứng minh trong (P) có một đường thẳng a mà a ⊥ (Q).
- Chứng minh ((P), (Q)) = 90°
* Chứng minh đường thẳng vuông góc với mặt phẳng
Để chứng minh d ⊥ (P), ta có thể chứng minh bởi một trong các cách sau:
- Chứng minh d ⊂ (Q) với (Q) ⊥ (P) và d vuông góc với giao tuyến c của (P) và (Q).
- Chứng minh d = (Q) ∩ (R) với (Q) ⊥ (P) và (R) ⊥ (P).
- Sử dụng các cách chứng minh đã biết ở phần trước.
*Lời giải:
* Chứng minh hai mặt phẳng vuông góc
Để chứng minh (P) ⊥ (Q), ta có thể chứng minh bởi một trong các cách sau:
- Chứng minh trong (P) có một đường thẳng a mà a ⊥ (Q).
- Chứng minh ((P), (Q)) = 90°
* Chứng minh đường thẳng vuông góc với mặt phẳng
Để chứng minh d ⊥ (P), ta có thể chứng minh bởi một trong các cách sau:
- Chứng minh d ⊂ (Q) với (Q) ⊥ (P) và d vuông góc với giao tuyến c của (P) và (Q).
- Chứng minh d = (Q) ∩ (R) với (Q) ⊥ (P) và (R) ⊥ (P).
- Sử dụng các cách chứng minh đã biết ở phần trước.

Ta có: SA ⊥ (ABCD) và BD ⊂ (ABCD) nên SA ⊥ BD.
Vì ABCD là hình thoi nên BD ⊥ AC.
Ta có: BD ⊥ SA, BD ⊥ AC và SA ∩ AC = A trong (SAC).
Suy ra BD ⊥ (SAC).
Mà BD ⊂ (SBD) nên (SAC) ⊥ (SBD).
*Một số lý thuyết cần nhớ về hai mặt phẳng vuông góc:
1. Định nghĩa
Hai mặt phẳng vuông góc là hai mặt phẳng có góc giữa của chúng bằng
2. Điều kiện
Hai mặt phẳng vuông góc với nhau khi và chỉ khi một mặt phẳng có chứa đường thẳng vuông góc với mặt phẳng còn lại
3. Tính chất
- Trong trường hợp nếu 2 mặt phẳng vuông góc với nhau thì bất kì đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến của 2 mặt phẳng thì sẽ vuông góc với mặt phẳng kia
- Nếu mặt phẳng (A), (B) vuông góc với nhau thì đường thẳng a đi qua điểm H (với điểm H nằm trên mặt phẳng A) và vuông góc với (B) sẽ nằm trong (A).
- Nếu hai mặt phẳng cắt nhau và 2 mặt phẳng này cùng vuông góc với mặt phẳng thứ 3 thì giao tuyến của chúng vuông góc với mặt phẳng còn lại.
Xem thêm các bài viết liên quan hay, chi tiết:
50 Bài tập Mặt phẳng vuông góc Toán 11 mới nhất
Trắc nghiệm Hai mặt phẳng vuông góc có đáp án (Thông hiểu)
TOP 40 câu Trắc nghiệm Hai mặt phẳng vuông góc (có đáp án 2023) – Toán 11
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho hình chóp S.ABC có SA ⊥ SB, SB ⊥ SC, SC ⊥ SA. Chứng minh rằng:
a) (SAB) ⊥ (SBC);
Cho hình chóp S.ABC có SA ⊥ SB, SB ⊥ SC, SC ⊥ SA. Chứng minh rằng:
a) (SAB) ⊥ (SBC);
Câu 3:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt phẳng (SAB) vuông góc với mặt đáy, tam giác SAB vuông cân tại S. Gọi M là trung điểm của AB. Chứng minh rằng:
a) SM ⊥ (ABCD);
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt phẳng (SAB) vuông góc với mặt đáy, tam giác SAB vuông cân tại S. Gọi M là trung điểm của AB. Chứng minh rằng:
a) SM ⊥ (ABCD);
Câu 4:
Nêu ví dụ trong thực tiễn minh họa hình ảnh hai mặt phẳng vuông góc.
Nêu ví dụ trong thực tiễn minh họa hình ảnh hai mặt phẳng vuông góc.
Câu 5:
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hai mặt phẳng (A’AB) và (A’AC) cùng vuông góc với (ABC).
a) Chứng minh rằng AA’ ⊥ (ABC).
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh cùng bằng a, hai mặt phẳng (A’AB) và (A’AC) cùng vuông góc với (ABC).
a) Chứng minh rằng AA’ ⊥ (ABC).
Câu 6:
Cho một đường thẳng không vuông góc với mặt phẳng cho trước. Chứng minh rằng tồn tại duy nhất một mặt phẳng chứa đường thẳng đó và vuông góc với mặt phẳng đã cho.
Cho một đường thẳng không vuông góc với mặt phẳng cho trước. Chứng minh rằng tồn tại duy nhất một mặt phẳng chứa đường thẳng đó và vuông góc với mặt phẳng đã cho.
Câu 7:
Chứng minh: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Chứng minh: Nếu hai mặt phẳng vuông góc với nhau thì mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
Câu 8:
Để công trình xây dựng được an toàn và bền vững, người ta thường xây tường nhà vuông góc với nền nhà (Hình 44).

Hình ảnh tường nhà vuông góc với nền nhà gợi nên khái niệm nào trong hình học?
Để công trình xây dựng được an toàn và bền vững, người ta thường xây tường nhà vuông góc với nền nhà (Hình 44).

Hình ảnh tường nhà vuông góc với nền nhà gợi nên khái niệm nào trong hình học?
Câu 9:
Trong Hình 54, hai bìa của cuốn sách gợi nên hình ảnh hai mặt phẳng vuông góc với mặt bàn. Hãy dự đoán xem gáy sách có vuông góc với mặt bàn hay không.
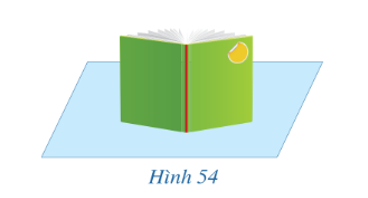
Trong Hình 54, hai bìa của cuốn sách gợi nên hình ảnh hai mặt phẳng vuông góc với mặt bàn. Hãy dự đoán xem gáy sách có vuông góc với mặt bàn hay không.

Câu 10:
Quan sát ba mặt phẳng (P), (Q), (R) ở Hình 57, chỉ ra hai cặp mặt phẳng mà mỗi cặp gồm hai mặt phẳng vuông góc với nhau. Hãy sử dụng kí hiệu để viết những kết quả đó.

Quan sát ba mặt phẳng (P), (Q), (R) ở Hình 57, chỉ ra hai cặp mặt phẳng mà mỗi cặp gồm hai mặt phẳng vuông góc với nhau. Hãy sử dụng kí hiệu để viết những kết quả đó.

Câu 11:
Cho hình chóp S.OAB thoả mãn (AOS) ⊥ (AOB), (Hình 51).
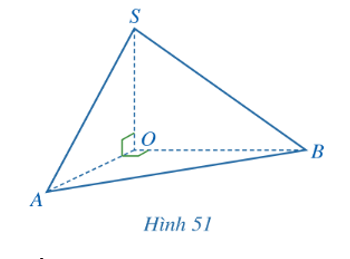
a) Giao tuyến của hai mặt phẳng (AOS) và (AOB) là đường thẳng nào?
Cho hình chóp S.OAB thoả mãn (AOS) ⊥ (AOB), (Hình 51).

a) Giao tuyến của hai mặt phẳng (AOS) và (AOB) là đường thẳng nào?
Câu 12:
b) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt phẳng còn lại.
b) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt phẳng còn lại.
Câu 14:
Cho tứ diện ABCD có (ABD) ⊥ (BCD) và CD ⊥ BD. Chứng minh rằng tam giác ACD vuông.
Cho tứ diện ABCD có (ABD) ⊥ (BCD) và CD ⊥ BD. Chứng minh rằng tam giác ACD vuông.
Câu 15:
Chứng minh các định lí sau:
a) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó;
Chứng minh các định lí sau:
a) Nếu hai mặt phẳng (phân biệt) cùng vuông góc với mặt phẳng thứ ba thì song song với nhau hoặc cắt nhau theo một giao tuyến vuông góc với mặt phẳng thứ ba đó;


