Câu hỏi:
11/10/2024 1,618Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a; AD = 2a (a > 0). Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy. Biết mặt phẳng (SAC) hợp với (ABCD) một góc . Tính khoảng cách giữa CD và SB.
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
*Phương pháp giải:
Phương pháp 1: Chọn mặt phẳng (α) chứa đường thẳng và song song với '. Khi đó d(, ') = d(', (α)).
Phương pháp 2: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.
Phương pháp 3: Dựng đoạn vuông góc chung và tính độ dài đoạn đó.
*Lời giải:
*Một số lý thuyết thêm về khoảng cách:
Đường thẳng cắt hai đường thẳng chéo nhau a, b và vuông góc với cả hai đường thẳng đó được gọi là đường vuông góc chung của a và b.
Nếu đường vuông góc chung cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b.
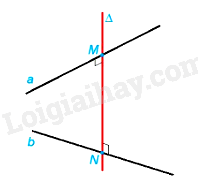
Nhận xét:
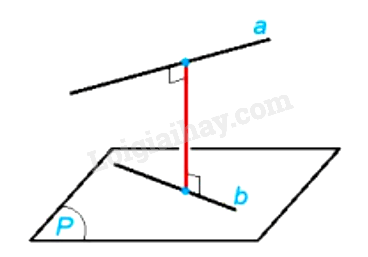
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
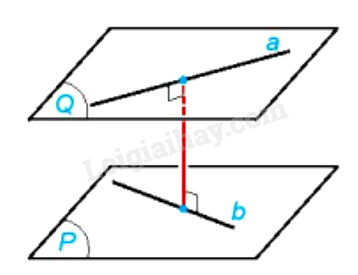
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song, tương ứng chứa hai đường thẳng đó.
Xem thêm các bài viết liên quan hay, chi tiết:
50 bài toán về khoảng cách trong không gian (có đáp án 2024) – Toán 12
TOP 40 câu Trắc nghiệm Khoảng cách (có đáp án 2023) – Toán 11
Trắc nghiệm Hình học 11 có đáp án
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc . Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Góc giữa mặt phẳng (SAB) và (ABCD) bằng . Khoảng cách từ B đến mặt phẳng (SCD) bằng
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a, DC = a. Điểm I là trung điểm đoạn AD, mặt phẳng (SIB) và (SIC) cùng vuông góc với mặt phẳng (ABCD) . Mặt phẳng (SBC) tạo với mặt phẳng (ABCD) một góc . Tính khoảng cách từ D đến (SBC) theo a.
Câu 3:
Cho hình chóp S.ABCD, đáy là hình thang vuông tại A và B, biết AB = BC = a, AD = 2a, SA = và SA(ABCD). Gọi M và N lần lượt là trung điểm của SB, SA. Tính khoảng cách từ M đến (NCD) theo a.
Câu 4:
Cho tứ diện ABCD có DA = DB = DC tam giác ABC vuông tại A, AB = a, . Ngoài ra DBC là tam giác vuông. Tính khoảng cách giữa hai đường thẳng AM và CD với M là trung điểm của BC.
Câu 5:
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AD = 2a, AA' = a. Gọi M là điểm trên đoạn AD với = 3. Gọi x là độ dài khoảng cách giữa hai đường thẳng AD', B'C và y là độ dài khoảng cách từ M đến mặt phẳng (AB'C). Tính giá trị xy.
Câu 6:
Cho hình chóp S.ABCD có đáy là hình bình hành với AB = 2a; ; . Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trọng tâm G của tam giác BCD, biết SG = 2a. Khoảng cách giữa hai đường thẳng AC và SB theo a là:
Câu 7:
Cho hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết AC = 2a; BD = 4a. Tính theo a khoảng cách giữa hai đường thẳng AD và SC.
Câu 8:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = a, SA vuông góc với mặt phẳng (ABC), góc giữa đường thẳng SC và mặt phẳng (ABC) bằng . Khoảng cách giữa hai đường thẳng SB và AC.
Câu 9:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = 4a, BC = 3a. Gọi I là trung điểm của AB, hai mặt phẳng (SIC) và (SIB) cùng vuông góc với (ABC), góc giữa hai mặt phẳng (SAC) và (ABC) bằng . Khoảng cách giữa hai đường thẳng SB và AC theo a là:


