Câu hỏi:
22/07/2024 187
Cho hình chóp S.ABCD có ABCD là hình thang đáy lớn AD. Gọi E, F lần lượt là hai điểm trên hai cạnh SB, SD.
a) Tìm giao điểm của EF với (SAC).
b) Tìm giao điểm của BC với (AEF).
Cho hình chóp S.ABCD có ABCD là hình thang đáy lớn AD. Gọi E, F lần lượt là hai điểm trên hai cạnh SB, SD.
a) Tìm giao điểm của EF với (SAC).
b) Tìm giao điểm của BC với (AEF).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
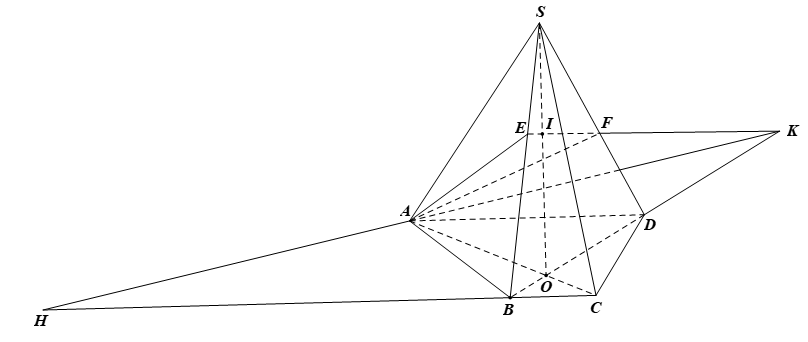
a) ⦁ Trong mặt phẳng (ABCD), gọi O = AC ∩ BD.
Ta có O ∈ AC, AC ⊂ (SAC) nên O ∈ (SAC)
O ∈ BD, BD ⊂ (SBD) nên O ∈ (SBD)
Do đó O ∈ (SAC) ∩ (SBD)
⦁ Lại có S ∈ (SAC) và S ∈ (SBD) nên S ∈ (SAC) ∩ (SBD)
Suy ra (SAC) ∩ (SBD) = SO.
Trong mặt phẳng (SBD), gọi I = EF ∩ SO.
Ta có I ∈ SO, SO ⊂ (SAC) nên I ∈ (SAC)
Vậy EF ∩ (SAC) = I.
b) ⦁ Trong mặt phẳng (SBD), gọi K = EF ∩ BD.
Ta có K ∈ EF, EF ⊂ (AEF) nên K ∈ (AEF);
K ∈ BD, BD ⊂ (ABCD) nên K ∈ (ABCD)
Do đó K ∈ (ABCD) ∩ (AEF).
Lại có A ∈ (ABCD) và ∈ (AEF) nên A = (ABCD) ∩ (AEF).
Suy ra (ABCD) ∩ (AEF) = AK.
⦁ Trong mặt phẳng (ABCD), gọi H = BC ∩ AK.
Ta có H ∈ AK, AK ⊂ (AEF) nên H ∈ (AEF).
Vậy BC ∩ (AEF) = H.

a) ⦁ Trong mặt phẳng (ABCD), gọi O = AC ∩ BD.
Ta có O ∈ AC, AC ⊂ (SAC) nên O ∈ (SAC)
O ∈ BD, BD ⊂ (SBD) nên O ∈ (SBD)
Do đó O ∈ (SAC) ∩ (SBD)
⦁ Lại có S ∈ (SAC) và S ∈ (SBD) nên S ∈ (SAC) ∩ (SBD)
Suy ra (SAC) ∩ (SBD) = SO.
Trong mặt phẳng (SBD), gọi I = EF ∩ SO.
Ta có I ∈ SO, SO ⊂ (SAC) nên I ∈ (SAC)
Vậy EF ∩ (SAC) = I.
b) ⦁ Trong mặt phẳng (SBD), gọi K = EF ∩ BD.
Ta có K ∈ EF, EF ⊂ (AEF) nên K ∈ (AEF);
K ∈ BD, BD ⊂ (ABCD) nên K ∈ (ABCD)
Do đó K ∈ (ABCD) ∩ (AEF).
Lại có A ∈ (ABCD) và ∈ (AEF) nên A = (ABCD) ∩ (AEF).
Suy ra (ABCD) ∩ (AEF) = AK.
⦁ Trong mặt phẳng (ABCD), gọi H = BC ∩ AK.
Ta có H ∈ AK, AK ⊂ (AEF) nên H ∈ (AEF).
Vậy BC ∩ (AEF) = H.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ diện ABCD. Gọi E, F, G lần lượt là các điểm thuộc ba cạnh AB, AC, BD sao cho EF cắt BC tại I, AD cắt EG tại H. Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Cho tứ diện ABCD. Gọi E, F, G lần lượt là các điểm thuộc ba cạnh AB, AC, BD sao cho EF cắt BC tại I, AD cắt EG tại H. Chứng minh ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Câu 2:
Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho EB > AE, AF > FC, BG > GD. Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD).
Cho tứ diện ABCD. Trên các cạnh AB, AC, BD lần lượt lấy các điểm E, F, G sao cho EB > AE, AF > FC, BG > GD. Tìm giao tuyến của các cặp mặt phẳng (EFG) và (ACD), (EFG) và (BCD), (EFG) và (ABD).
Câu 3:
Cho hình chóp S.ABCD. Gọi D, E, F lần lượt là ba điểm trên ba cạnh SA, SB, SC sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I, J, K thẳng hàng.
Cho hình chóp S.ABCD. Gọi D, E, F lần lượt là ba điểm trên ba cạnh SA, SB, SC sao cho DE cắt AB tại I, EF cắt BC tại J, FD cắt CA tại K. Chứng minh ba điểm I, J, K thẳng hàng.


