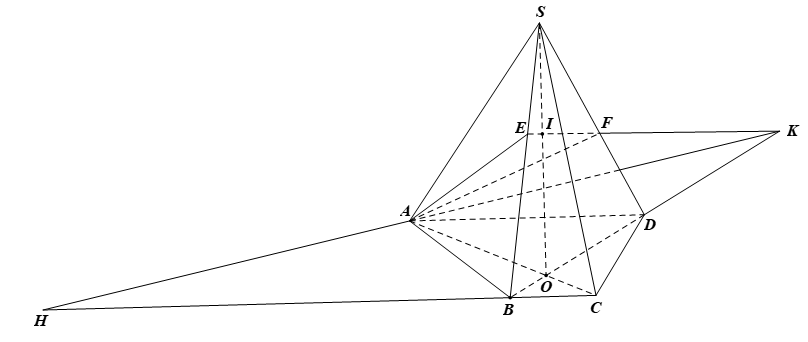
a) ⦁ Trong mặt phẳng (ABCD), gọi O = AC ∩ BD.

Ta có O ∈ AC, AC ⊂ (SAC) nên O ∈ (SAC)

          O ∈ BD, BD ⊂ (SBD) nên O ∈ (SBD)

Do đó O ∈ (SAC) ∩ (SBD)

⦁ Lại có S ∈ (SAC) và S ∈ (SBD) nên S ∈ (SAC) ∩ (SBD)

Suy ra (SAC) ∩ (SBD) = SO.

Trong mặt phẳng (SBD), gọi I = EF ∩ SO.

Ta có I ∈ SO, SO ⊂ (SAC) nên I ∈ (SAC)

Vậy EF ∩ (SAC) = I.

b) ⦁ Trong mặt phẳng (SBD), gọi K = EF ∩ BD.

Ta có K ∈ EF, EF ⊂ (AEF) nên K ∈ (AEF);

          K ∈ BD, BD ⊂ (ABCD) nên K ∈ (ABCD)

Do đó K ∈ (ABCD) ∩ (AEF).

Lại có A ∈ (ABCD) và ∈ (AEF) nên A = (ABCD) ∩ (AEF).

Suy ra (ABCD) ∩ (AEF) = AK.

⦁ Trong mặt phẳng (ABCD), gọi H = BC ∩ AK.

Ta có H ∈ AK, AK ⊂ (AEF) nên H ∈ (AEF).

Vậy BC ∩ (AEF) = H.

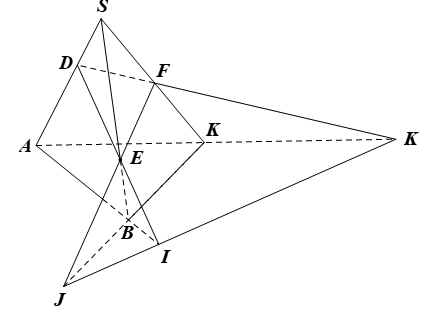
Ta có: I là giao điểm của DE và AB.

Suy ra:

⦁ I ∈ DE, mà DE ⊂ (DEF) nên I ∈ (DEF);

⦁ I ∈ AB, mà AB ⊂ (ABC) nên I ∈ (ABC).

Do đó I ∈ (DEF) ∩ (ABC).

Tương tự, ta có J, K cũng thuộc giao tuyến của hai mặt phẳng (DEF), (ABC).

Vậy I, J, K thẳng hàng.

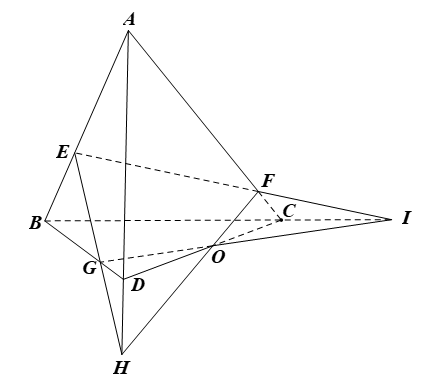
Gọi O là giao điểm của HF và IG.

Ta có:

⦁ O ∈ HF, mà HF ⊂ (ACD), suy ra O ∈ (ACD);

⦁ O ∈ IG, mà IG ⊂ (BCD), suy ra O ∈ (BCD).

Do đó, O ∈ (ACD) ∩ (BCD) (1)

Mặt khác, (ACD) ∩ (BCD) = CD (2)

Từ (1) và (2), suy ra O ∈ CD.

Lại có O = HF ∩ IG nên O là giao điểm của ba đường thẳng CD, IG, HF.

Vậy ba đường thẳng CD, IG, HF cùng đi qua một điểm.

* Một số lý thuyết và bài tập liên quan: 

- Định nghĩa về ba đường thẳng đồng quy được diễn giải như sau: “Cho ba đường thẳng lần lượt là a, b, c không trùng với nhau. Nếu ba đường thẳng a,b,c cùng đi qua một điểm O nào đó thì ta sẽ gọi đó là đồng quy.

VD: Cho ba đường thẳng d₁, d₂, d₃ không cùng nằm trong một mặt phẳng và cắt nhau từng đôi một. Chứng minh ba đường thẳng trên đồng quy.

Lời giải:

Gọi d₁, d₂, d₃ là ba đường thẳng đã cho.

Gọi $I=d_1\cap d_2$ suy ra  $\left\{\begin{array}{l}I\in d_1\\ I\in d_2\end{array}\right.$

Ta chứng minh $I\in d_3$. Thật vậy,

Gọi (β) là mặt phẳng chứa hai đường thẳng cắt nhau d₁, d₃.

(γ) là mặt phẳng chứa hai đường thẳng cắt nhau d₂, d₃.

Do ba đường thẳng không cùng nằm trong một mặt phẳng nên (β) và (γ) phân biệt.

Ngoài ra $\left\{\begin{array}{l}{d}_3\subset \left(\beta \right)\\ d_3\subset \left(\gamma \right)\end{array}\right.$ suy ra $\left(\beta \right)\cap \left(\gamma \right)=d_3$

$I\in d_1\subset \left(\beta \right)$ suy ra  $I\in \left(\beta \right)=\left(d_1,d_3\right)$

$I\in d_2\subset \left(\gamma \right)$ suy ra  $I\in \left(\gamma \right)=\left(d_2,d_3\right)$

Từ đó suy ra,  $I\in \left(\beta \right)\cap \left(\gamma \right)=d_3$

Vậy d₁, d₂, d₃ đồng quy.

Cách khác:

Gọi (P) là mặt phẳng chứa hai đường thẳng cắt nhau d₁, d₂

Goi $d_3\cap d_1=M;d_3\cap d_2=N$.

$M\in d_1$, mà $d_1\subset \left(P\right)$ suy ra $M\in \left(P\right)$

$N\in {\text{d}}_2$, mà ${\text{d}}_2\subset \left(\text{P}\right)$ suy ra $\text{N}\in \left(\text{P}\right)$

Nếu $\text{M}\ne \text{N}$ suy ra d₃ có hai điểm M, N cùng thuộc (P)

Suy ra $d_3\subset \left(P\right)$

Suy ra d₁, d₂, d₃ đồng phẳng (trái với giả thiết d₁, d₂, d₃ không đồng phẳng)

Suy ra $M\equiv N$ là điểm thuộc cả d₁, d₂, d₃

Vậy d₁, d₂, d₃ đồng quy.

Xem thêm các bài viết liên quan hay, chi tiết:

Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Nhận biết)

100 câu trắc nghiệm Đường thẳng, Mặt phẳng trong không gian nâng cao (phần 1) 

50 bài tập Đại cương về đường thẳng (có đáp án 2024) và cách giải

 

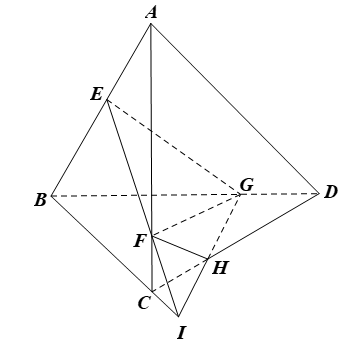
⦁ Ta có EF ⊂ (ABC) và EF ⊂ (EFG) nên (EFG) ∩ (ABC) = EF.

⦁ Trong mặt phẳng (ABC), gọi I là giao điểm của EF và BC.

Trong mặt phẳng (BCD), gọi H là giao điểm của IG và CD.

Ta có H ∈ IG, mà IG ⊂ (EFG) nên H ∈ (EFG)

Lại có F ∈ (EFG) nên FH ⊂ (EFG) (1)

Ta cũng có F ∈ AC, mà AC ⊂ (ACD)

                  H ∈ CD, mà CD ⊂ (ACD)

Do đó FH ⊂ (ACD) (2)

Từ (1) và (2) suy ra (EFG) ∩ (ACD) = FH.

⦁ Tương tự, ta cũng có:

HG ⊂ (EFG) và HG ⊂ (BCD) nên (EFG) ∩ (BCD) = HG;

GE ⊂ (EFG) và GE ⊂ (ABD) nên (EFG) ∩ (ABD) = GE.

Vậy (EFG) ∩ (ACD) = FH, (EFG) ∩ (BCD) = HG, (EFG) ∩ (ABD) = GE.