Câu hỏi:
23/07/2024 268
Cho hai hàm số f(x) và g(x) có limx→+∞f(x)=3 và limx→+∞[f(x)+2g(x)]=7.
Tìm limx→+∞2f(x)+g(x)2f(x)−g(x).
Cho hai hàm số f(x) và g(x) có limx→+∞f(x)=3 và limx→+∞[f(x)+2g(x)]=7.
Tìm limx→+∞2f(x)+g(x)2f(x)−g(x).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm giá trị của các tham số a và b, biết rằng:
a) limx→2ax+bx−2=5; b)limx→1a√x+bx−1=3.
Tìm giá trị của các tham số a và b, biết rằng:
a) limx→2ax+bx−2=5; b)limx→1a√x+bx−1=3.
Câu 2:
Cho hàm số f(x)={2x+1, x≤1√x2+a, x>1.
Tìm giá trị của tham số a sao cho tồn tại giới hạn limx→1f(x).
Cho hàm số f(x)={2x+1, x≤1√x2+a, x>1.
Tìm giá trị của tham số a sao cho tồn tại giới hạn limx→1f(x).
Câu 3:
Mỗi giới hạn sau có tồn tại không? Nếu có, hãy tìm giới hạn đó.
a) limx→0x2|x|; b)limx→2x2−2x|x−2|.
Mỗi giới hạn sau có tồn tại không? Nếu có, hãy tìm giới hạn đó.
a) limx→0x2|x|; b)limx→2x2−2x|x−2|.
Câu 4:
Sử dụng định nghĩa, tìm các giới hạn sau:
a) limx→−1(x3−3x); b) limx→2√2x+5; c)limx→+∞4−x2x+1.
Sử dụng định nghĩa, tìm các giới hạn sau:
a) limx→−1(x3−3x); b) limx→2√2x+5; c)limx→+∞4−x2x+1.
Câu 5:
Cho hai hàm số f(x) và g(x) có limx→4f(x)=2 và limx→4g(x)=−3.Tìm các giới hạn:
a)limx→4[g(x)−3f(x)]; b)limx→42f(x)⋅g(x)[f(x)+g(x)]2.
Cho hai hàm số f(x) và g(x) có limx→4f(x)=2 và limx→4g(x)=−3.Tìm các giới hạn:
a)limx→4[g(x)−3f(x)]; b)limx→42f(x)⋅g(x)[f(x)+g(x)]2.
Câu 6:
Tính các giới hạn sau:
a)limx→−∞(x3+2x2−1); b) limx→+∞x3+2x23x2+1; c)limx→−∞√x2−2x+3.
Tính các giới hạn sau:
a)limx→−∞(x3+2x2−1); b) limx→+∞x3+2x23x2+1; c)limx→−∞√x2−2x+3.
Câu 7:
Tìm các giới hạn sau:
a) limx→−2x2−4x+2; b) limx→1x3−11−x;
c) limx→3x2−4x+3x−3; d)limx→−22−√x+6x+2;
e) limx→0x√x+1−1; g)limx→2x2−4x+4x2−4.
Tìm các giới hạn sau:
a) limx→−2x2−4x+2; b) limx→1x3−11−x;
c) limx→3x2−4x+3x−3; d)limx→−22−√x+6x+2;
e) limx→0x√x+1−1; g)limx→2x2−4x+4x2−4.
Câu 8:
Cho hàm số f(x)={3x+4, x≤−13−2x2, x>−1.
Tìm các giới hạn limx→−1+f(x),limx→−1−f(x) và limx→−1f(x).
Cho hàm số f(x)={3x+4, x≤−13−2x2, x>−1.
Tìm các giới hạn limx→−1+f(x),limx→−1−f(x) và limx→−1f(x).
Câu 9:
Tìm các giới hạn sau:
a) limx→+∞xx+4; b)limx→−∞2x2+1(2x+1)2;
c) limx→−∞3x+1√x2−2x; d)limx→+∞(x−√x2+2x).
Tìm các giới hạn sau:
a) limx→+∞xx+4; b)limx→−∞2x2+1(2x+1)2;
c) limx→−∞3x+1√x2−2x; d)limx→+∞(x−√x2+2x).
Câu 10:
Trong mặt phẳng toạ độ Oxy, cho điểm M(t, t2), t > 0, nằm trên đường parabol y = x2. Đường trung trực của đoạn thẳng OM cắt trục tung tại N. Điểm N dần đến điểm nào khi điểm M dần đến điểm O?
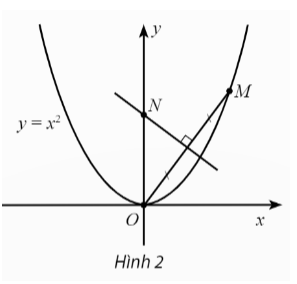
Trong mặt phẳng toạ độ Oxy, cho điểm M(t, t2), t > 0, nằm trên đường parabol y = x2. Đường trung trực của đoạn thẳng OM cắt trục tung tại N. Điểm N dần đến điểm nào khi điểm M dần đến điểm O?

Câu 11:
Tìm các giới hạn sau:
a) limx→−3(8+3x−x2); b)limx→2[(5x−1)(2−4x)];
c)limx→−2x2−x(2x+1)2; d)limx→−1√10−2x2.
Tìm các giới hạn sau:
a) limx→−3(8+3x−x2); b)limx→2[(5x−1)(2−4x)];
c)limx→−2x2−x(2x+1)2; d)limx→−1√10−2x2.


