Câu hỏi:
08/01/2025 814
Cho cos2x=14. Tính: A=cos(x+π6)cos(x−π6); B=sin(x+π3)sin(x−π3).
Cho cos2x=14. Tính: A=cos(x+π6)cos(x−π6); B=sin(x+π3)sin(x−π3).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
*Lời giải:
Ta có:
A=cos(x+π6)cos(x−π6)
=12[cos(x+π6+x−π6)+cos(x+π6−x+π6)]
=12[cos2x+cosπ3]
=12[14+12]=38.
B=sin(x+π3)sin(x−π3)
=−12[cos(x+π3+x−π3)−cos(x+π3−x+π3)]
=−12[cos2x−cos2π3]
=−12[14−(−12)]=−38.
Vậy A=38,B=−38.
*Phương pháp giải:
áp dụng công thức biến đổi lượng giác để biến đổi: Công thức biến đổi tích thành tổng
*Lý thuyết nắm thêm
I. Công thức cộng
sin(a+b)=sinacosb+cosasinbsin(a−b)=sinacosb−cosasinbcos(a+b)=cosacosb−sinasinbcos(a−b)=cosacosb+sinasinbtan(a+b)=tana+tanb1−tanatanbtan(a−b)=tana−tanb1+tanatanb
II. Công thức nhân đôi
sin2a=2sinacosacos2a=cos2a−sin2a=2cos2a−1=1−2sin2atan2a=2tana1−tan2a
Suy ra, công thức hạ bậc:
sin2a=1−cos2a2,cos2a=1+cos2a2
III. Công thức biến đổi tích thành tổng
cosacosb=12[cos(a+b)+cos(a−b)]sinasinb=12[cos(a−b)−cos(a+b)]sinacosb=12[sin(a+b)+sin(a−b)]
IV. Công thức biến đổi tổng thành tích
cosa+cosb=2cosa+b2cosa−b2cosa−cosb=−2sina+b2sina−b2sina+sinb=2sina+b2cosa−b2sina−sinb=2cosa+b2sina−b2
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Các phép biến đổi lượng giác – Toán 11 Cánh diều
TOP 12 câu Trắc nghiệm Các phép biến đổi lượng giác (Cánh diều 2024) có đáp án - Toán 11
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 9:
Sử dụng công thức cộng, rút gọn mỗi biểu thức sau:
cos(a + b) + cos(a – b); cos(a + b) – cos(a – b); sin(a + b) + sin(a – b).
Sử dụng công thức cộng, rút gọn mỗi biểu thức sau:
cos(a + b) + cos(a – b); cos(a + b) – cos(a – b); sin(a + b) + sin(a – b).
Câu 10:
Có hai chung cư cao tầng I và II xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư II người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư I mà camera có thể quan sát được (Hình 18). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư I). Biết rằng chiều cao của chung cư II là CK = 32 m, AH = 6 m, BH = 24 m (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
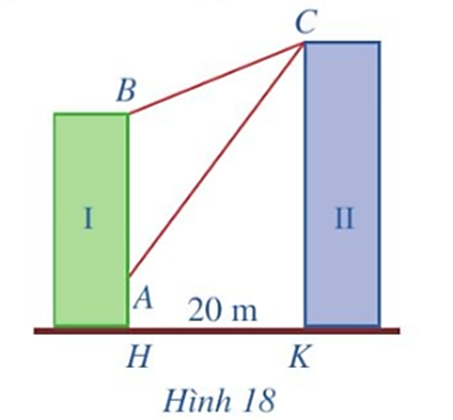
Có hai chung cư cao tầng I và II xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư II người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư I mà camera có thể quan sát được (Hình 18). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư I). Biết rằng chiều cao của chung cư II là CK = 32 m, AH = 6 m, BH = 24 m (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Câu 11:
Tính:
A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°);
B=cos(b+π3)cos(π6−b)−sin(b+π3)sin(π6−b).
Tính:
A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°);
B=cos(b+π3)cos(π6−b)−sin(b+π3)sin(π6−b).
Câu 14:
Khi các biểu thức đều có nghĩa, hãy tính tan (a – b) bằng cách biến đổi tan(a−b)=tan[a+(−b)] và sử dụng công thức tan(a + b) có được ở bài trước
Khi các biểu thức đều có nghĩa, hãy tính tan (a – b) bằng cách biến đổi tan(a−b)=tan[a+(−b)] và sử dụng công thức tan(a + b) có được ở bài trước
Câu 15:
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m (Hình 17).
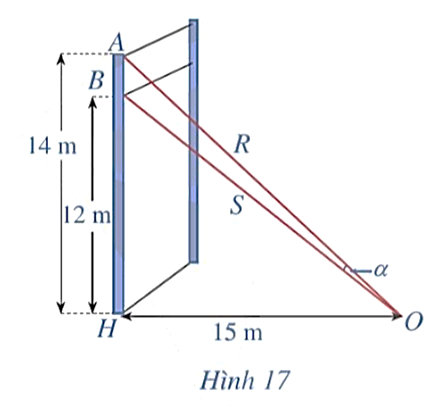 Tính tanα, ở đó α là góc giữa hai sợi cáp trên.
Tính tanα, ở đó α là góc giữa hai sợi cáp trên.
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m (Hình 17).



