Nội dung bài viết

    Xem thêm

    Vẽ đồ thị của các hàm số sau: y = 2x – 3

    Với giải câu hỏi 3 trang 51 sgk Toán lớp 9 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 2,812 05/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải toán 9 Bài 3: Đồ thị của hàm số y = ax + b

    Video Giải Câu hỏi 3 trang 51 Toán lớp 9 Tập 1

    Câu hỏi 3 trang 51 Toán lớp 9 Tập 1: Vẽ đồ thị của các hàm số sau:

    a) y = 2x – 3;

    b) y = -2x + 3.

    *Lời giải:

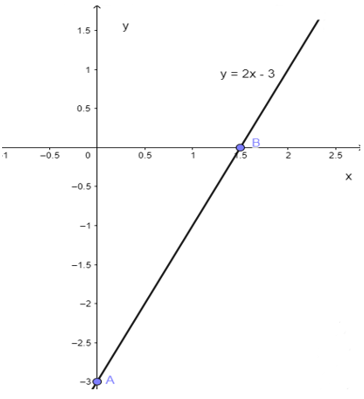
    a) y = 2x – 3

    Cho x = 0 ⇒y = -3 Điểm A (0; -3)

    Cho y = 0 ⇒x = 32. Điểm B(32;0)

    Đồ thị hàm số y = 2x – 3 là đường thẳng đi qua hai điểm A (0; -3) và B( 32;0)

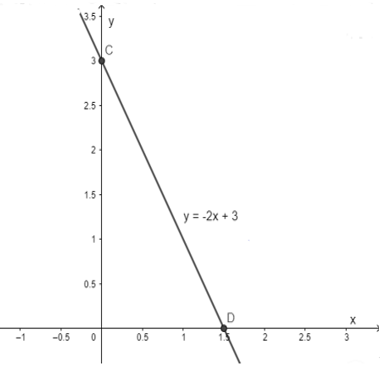
    Tài liệu VietJack

    b) y = -2x + 3

    Cho x = 0 ⇒y = 3 Điểm C (0; 3)

    Cho y = 0 ⇒x = Điểm D (32;0)

    Đồ thị hàm số y = 2x – 3 là đường thẳng đi qua hai điểm C (0; 3) và D (32;0 ).

    Tài liệu VietJack

    *Phương pháp giải:

    + Điểm M(xo; yo) thuộc đồ thị hàm số bậc nhất y = ax + b ⇔ yo = axo + b.

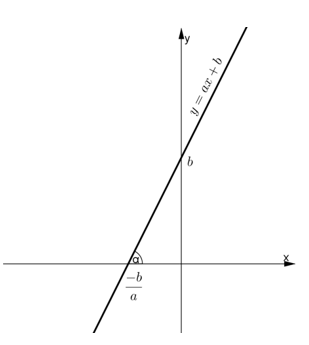
    + Đồ thị hàm số y = ax + b là một đường thẳng đi qua hai điểm A(0; b) và B(-b/a;0) .

    + a được gọi là hệ số góc của đường thẳng y = ax + b.

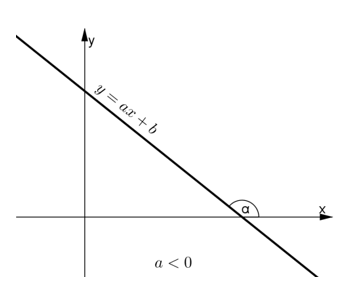
    Góc α là góc tạo bởi đường thẳng y = ax + b và hướng dương của trục Ox.

    Cách làm bài toán Đồ thị hàm số lớp 9 cực hay (có lời giải) | Chuyên đề Toán 9

    Nếu a > 0 thì α < 90o

    Cách làm bài toán Đồ thị hàm số lớp 9 cực hay (có lời giải) | Chuyên đề Toán 9

    Nếu a < 0 thì α > 90o

    Cách làm bài toán Đồ thị hàm số lớp 9 cực hay (có lời giải) | Chuyên đề Toán 9

    *Lý thuyết cần nắm và các dạng bài toán về hàm số bậc nhất và cách vẽ đồ thị:

    Đồ thị hàm số bậc nhất

    Hàm số bậc nhất y = ax + b với a≠0 có đồ thị là một đường thẳng.

    - Cắt trục tung tại điểm có tung độ bằng b;

    - Song song với đường thẳng y = ax nếu b ≠ 0; trùng với y = ax nếu b = 0.

    Kí hiệu là d: y = ax + b.

    Cách vẽ đồ thị hàm số bậc nhất

    Xét đường thẳng d: y = ax + b với a≠0

    Bước 1: Xét hệ số b

    - Nếu b = 0 ta có d: y = ax đi qua gốc tọa độ O(0; 0) và điểm A(1; a)

    - Nếu b≠0 thì d đi qua hai điểm A(0; b) và B−ba;0

    Bước 2:

    - Nếu b = 0, ta vẽ đường thẳng d đi qua hai điểm O(0; 0) và A(1; a). Đường thẳng d là đồ thị hàm số.

    - Nếu b ≠ 0, ta vẽ đường thẳng đi qua hai điểm A(0; b) và B−ba;0. Đường thẳng d là đồ thị hàm số.

    Các dạng bài tập

    Dạng 1: Vẽ đồ thị hàm số bậc nhất

    Phương pháp giải: Xét đường thẳng d: y = ax + b với a≠0

    - Nếu b = 0 ta có d: y = ax đi qua gốc tọa độ O(0; 0) và điểm A(1; a)

    - Nếu b≠0 thì d đi qua hai điểm A(0; b) và B−ba;0.

    Dạng 2: Xác định điểm thuộc hay không thuộc đồ thị hàm số

    Phương pháp giải: Cho hàm số y = ax + b và M(m, n) với a≠ 0

    Cách 1: Ta biểu diễn điểm M và đồ thị hàm số d: y = ax +b trên cùng một hệ trục tọa độ

    Nếu điểm M thuộc đồ thị hàm số thì điểm đó nằm trên đường thẳng d

    Nếu điểm M không thuộc đồ thị hàm số thì điểm M không nằm trên đường thẳng d.

    Cách 2: Ta thay tọa độ điểm M vào hàm số

    Nếu am + b = n thì M thuộc đồ thị hàm số

    Nếu am + b ≠n thì M không thuộc đồ thị hàm số.

    Dạng 3: Xác định tọa độ giao điểm của hai đường thẳng

    Phương pháp giải: Cho hai đường thẳng d: y = ax + b và d’: y = a’x + b’ với a, a’≠ 0

    Để tìm tọa độ giao điểm d và d’ ta làm như sau:

    Cách 1: Phương pháp đại số:

    Bước 1: Xét phương trình hoành độ giao điểm của d và d’

    ax + b = a’x + b’

    Bước 2: Từ phương trình hoành độ giao điểm ta tìm được x, thay x vào d hoặc d’ để tìm y

    Bước 3: Kết luận giao điểm

    Cách 2: Dùng phương pháp tọa độ

    Bước 1: Vẽ d và d’ trên cùng một hệ trục tọa độ

    Bước 2 Từ hình vẽ xác định tọa độ giao điểm

    Bước 3: Kết luận giao điểm

    Xem thêm các bài viết liên quan hay, chi tiết:

    Hàm số bậc nhất và cách vẽ đồ thị hàm số bậc nhất (có đáp án 2024) - Toán 9

    Lý thuyết Đồ thị hàm số y = ax (mới 2024 + Bài Tập) – Toán 9

    TOP 40 câu Trắc nghiệm Đồ thị của hàm số y = ax + b (có đáp án 2024) – Toán 9

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 1 trang 49 Toán 9 Tập 1: Biểu diễn các điểm sau trên cùng một mặt phẳng...

    Câu hỏi 2 trang 49 Toán 9 Tập 1: Tính giá trị y tương ứng của các hàm số...

    Bài 15 trang 51 Toán 9 Tập 1: a) Vẽ đồ thị của các hàm số y = 2x...

    Bài 16 trang 51 Toán 9 Tập 1: a) Vẽ đồ thị của các hàm số y = x...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,812 05/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: