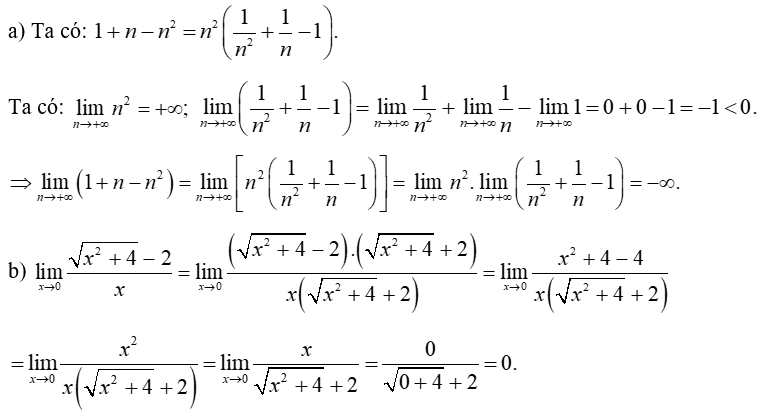TOP 10 đề thi Học kì 1 Toán lớp 11 (Chân trời sáng tạo) 2024 có đáp án

Chỉ từ 150k mua trọn bộ Đề thi Toán 11 Học kì 1 Chân trời sáng tạo bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi Học kì 1 Toán 11 (Chân trời sáng tạo) 2024 có đáp án

Sở Giáo dục và Đào tạo ...

Đề thi Học kì 1 - Chân trời sáng tạo

Năm học ....

Môn: Toán lớp 11

Thời gian làm bài: phút

Đề thi Học kì 1 Toán 11 Chân trời sáng tạo - (Đề số 1)

I. Trắc nghiệm (7 điểm)

Câu 1. Đổi góc \(\alpha \) có số đo \(\frac{{3\pi }}{5}\) sang độ ta được số đo bằng độ là

A. \(150^\circ .\)

B. \(135^\circ .\)

C. \(144^\circ .\)

D. \(108^\circ .\)

Câu 2. Đẳng thức nào dưới đây là đúng?

Câu 3. Tập giá trị của hàm số \(y = 2\cos 2x + 1\) là

A. \(\left[ { - 3;1} \right].\)

B. \(\left[ {1;3} \right].\)

C. \(\left[ { - 3; - 1} \right].\)

D. \(\left[ { - 1;3} \right].\)

Câu 4. Trong các hàm số sau, hàm số nào là hàm số lẻ?

A. \(y = \sqrt 3 \cos 3x.\)

B. \(y = \cos x.\)

C. \(y = \tan x.\)

D. \(y = {x^2}.\)

Câu 5. Nghiệm của phương trình \(\cot x = \sqrt 3 \) là

A. $x=-\frac{\pi }{3}+k\pi ,k\in \mathbb{Z}.$

B. $x=-\frac{\pi }{6}+k\pi ,k\in \mathbb{Z}.$

C. \(x = \frac{\pi }{3} + k\pi ,k \in \mathbb{Z}.\)

D. \(x = \frac{\pi }{6} + k\pi ,k \in \mathbb{Z}.\)

Câu 6. Nghiệm của phương trình \(\sin x = 0\) là

A. \(x = \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}.\)

B. \(x = k\pi ,k \in \mathbb{Z}.\)

C. \(x = k2\pi ,k \in \mathbb{Z}.\)

D. \(x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}.\)

Câu 7. Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {n^2} + 1.\) Dãy số \(\left( {{u_n}} \right)\) là dãy số

A. Không đổi.

B. Giảm.

C. Không tăng không giảm.

D. Tăng.

Câu 8. Cho dãy số \(\left( {{u_n}} \right)\), biết $\left\{\begin{array}{l}{u}_1=-1\\ u_{n+1}=u_n+3\end{array}\right.$ với \(n \ge 0\). Ba số hạng đầu tiên của dãy số đó lần lượt là những số nào dưới đây?

A. \( - 1;\,\,2;\,\,5\).

B. \( - 1;\,\,3;\,\,7\).

C. \(1;\,\,4;\,\,7\).

D. \(4;\,\,7;\,\,10\).

Câu 9. Cho dãy số \(\left( {{u_n}} \right)\), biết \({u_n} = \frac{{2n + 5}}{{5n - 4}}\). Số \(\frac{7}{{12}}\) là số hạng thứ mấy của dãy số?

A. \(9\).

B. \(6\).

C. \(10\).

D. \(8\).

Câu 10. Trong các dãy số sau, dãy số nào là một cấp số cộng?

A. \(1;\,\, - 4;\,\, - 9;\,\, - 14;\,\, - 19.\)

B. \(1;\,\,4;\,\,6;\,\,7;\,\,10.\)

C. \(1;\,\,0;\,\,0;\,\,0;\,\,0.\)

D. \(3;\,\,9;\,\,27;\,\,81;\,\,243.\)

Câu 11. Cho hình vẽ dưới đây. Các số hạng được viết trong các ô vuông từ trái sang phải tạo thành cấp số cộng. Giá trị của \(x\) trong hình vẽ đã cho là

A. \( - 4.\)

B. 7.

C. 4.

D. \( - 7.\)

Câu 12. Cho cấp số cộng \(\left( {{u_n}} \right)\) có $u_4=-12$ và \({u_{14}} = 18\). Tìm số hạng đầu tiên \({u_1}\) và công sai \(d\) của cấp số cộng đã cho.

A. $u_1=-22;d=3.$

B. $u_1=-21;d=3.$

C. $u_1=-21;d=-3.$

D. $u_1=-20;d=-3.$

Câu 13. Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{3}{2} \cdot {5^n}\). Khẳng định nào sau đây đúng?

A. \(\left( {{u_n}} \right)\) là cấp số nhân có công bội \(q = 5\) và số hạng đầu \({u_1} = \frac{3}{2}\).

B. \(\left( {{u_n}} \right)\) không phải là cấp số nhân.

C. \(\left( {{u_n}} \right)\) là cấp số nhân có công bội \(q = \frac{5}{2}\) và số hạng đầu \({u_1} = 3\).

D. \(\left( {{u_n}} \right)\) là cấp số nhân có công bội \(q = 5\) và số hạng đầu \({u_1} = \frac{{15}}{2}\).

Câu 14. Số hạng thứ \(5\) của một cấp số nhân \(\left( {{u_n}} \right)\) bằng \(162\) và số hạng thứ \(2\) bằng \(6.\)Số hạng thứ \(10\) của dãy số \(\left( {{u_n}} \right)\) là

A. \({u_{10}} = 39\,\,366.\)

B. \({u_{10}} = 118\,\,098.\)

C. \({u_{10}} = 972.\)

D. \({u_{10}} = 324.\)

Câu 15. Cho dãy số \(\left( {{u_n}} \right)\) thỏa mãn $\underset{n\to +\infty }{\lim }\left(4+u_n\right)=1.$ Giá trị của $\underset{n\to +\infty }{\lim }{u}_n$ bằng

A. \( - 3.\)

B. 1.

C. \(4.\)

D. \( - 4.\)

Câu 16. Trong các giới hạn sau giới hạn nào bằng 0.

A. \(\lim \frac{{1 - n}}{{2n + 1}}.\)

B. \(\lim {\left( {\frac{3}{2}} \right)^n}.\)

C. \(\lim {\left( {\frac{\pi }{4}} \right)^n}.\)

D. \(\lim {n^2}.\)

Câu 17. Chọn mệnh đề sai.

A. \(\lim \frac{3}{{n + 1}} = 0.\)

B. $\lim {\left(-2\right)}^n=+\infty .$

C. $\lim \left(\sqrt{n^2+2n+3}-n\right)=1.$

D. \(\lim \frac{1}{{{2^n}}} = 0.\)

Câu 18. Kết quả của giới hạn $\underset{x\to -1}{\lim }\left(x+1\right)$ là

A. 0.

B. \( - \infty .\)

C. 1.

D. \( + \infty .\)

Câu 19. Tính \(\mathop {\lim }\limits_{x \to 0} \frac{{x + 1}}{{{x^2}}}\).

A. 0.

B. \( - \infty .\)

C. 1.

D. \( + \infty .\)

Câu 20. Hàm số nào sau đây liên tục tại \(x = 2\)?

A. \(y = \frac{{2{x^2} + 6x + 1}}{{x + 2}}.\)

B. \(y = \frac{{x + 1}}{{x - 2}}.\)

C. \(y = \frac{1}{{{x^2} - 4}}.\)

D. \(y = \frac{{\sqrt x }}{{x - 2}}.\)

Câu 21. Hàm số nào sau đây liên tục trên \(\mathbb{R}\)?

A. \(y = \tan x.\)

B. \(y = \frac{1}{x}.\)

C. \(y = \sin x.\)

D. \(y = \cot x.\)

Câu 22. Yếu tố nào sau đây xác định một mặt phẳng duy nhất?

A. Ba điểm phân biệt.

B. Hai đường thẳng cắt nhau.

C. Bốn điểm phân biệt.

D. Một điểm và một đường thẳng.

Câu 23. Cho hình chóp tứ giác \(S.ABCD.\) Gọi \(O\) là giao điểm của \(AC\) và \[BD.\] Trong các mặt phẳng sau, điểm \(O\) không nằm trên mặt phẳng nào?

A. \(\left( {ABCD} \right).\)

B. \(\left( {SAD} \right).\)

C. \(\left( {SAC} \right).\)

D. \(\left( {SBD} \right).\)

Câu 24. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Trong không gian, qua một điểm và một đường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho.

B. Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau.

C. Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đồng quy.

D. Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đôi một song song.

Câu 25. Cho tứ diện \(ABCD.\) Gọi \(I,\,\,J\) lần lượt là trọng tâm của các tam giác \(ABC\) và \(ABD.\) Khẳng định nào sau đây đúng?

A. \(IJ\) cắt \(AB.\)

B. \(IJ\) song song \(AB.\)

C. \(IJ\) và \(CD\) là hai đường thẳng chéo nhau.

D. \(IJ\) song song \(CD.\)

Câu 26. Cho hai đường thẳng song song \(a,\,\,b\) và mặt phẳng \(\left( P \right)\). Mệnh đề nào dưới đây đúng?

A. Nếu \(a{\rm{//}}\left( P \right)\) thì \(b{\rm{//}}\left( P \right).\)

B. Nếu \(a\) cắt \(\left( P \right)\) thì \(b\) cắt \(\left( P \right).\)

C. Nếu \(a\) nằm trên \(\left( P \right)\) thì \(b{\rm{//}}\left( P \right).\)

D. Nếu \(a\) nằm trên \(\left( P \right)\) thì \(b\) nằm trên \(\left( P \right).\)

Câu 27. Cho hình chóp tứ \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Khẳng định nào sau đây sai?

A. \(CD{\rm{//}}\left( {SAB} \right).\)

B. \(AB{\rm{//}}\left( {SCD} \right).\)

C. \[BC{\rm{//}}\left( {SAD} \right).\]

D. \(AC{\rm{//}}\left( {SBD} \right).\)

Câu 28. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,\,\,N,\,\,P\) theo thứ tự lần lượt là trung điểm của \(SA,\,\,SB,\,\,SD.\) Khẳng định nào sau đây sai?

A. \(\left( {MNP} \right){\rm{//}}\left( {ABCD} \right).\)

B. \(\left( {MNP} \right){\rm{//}}\left( {SCD} \right).\)

C. \(MN{\rm{//}}\left( {ABCD} \right).\)

D. \(MP{\rm{//}}\left( {ABCD} \right).\)

Câu 29. Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(I,J,K\) lần lượt là trọng tâm tam giác \(ABC,ACC',AB'C'\). Mặt phẳng nào sau đây song song với \(\left( {IJK} \right)\)?

A. \(\left( {BC'A} \right).\)

B. \(\left( {AA'B} \right).\)

C. \(\left( {BB'C} \right).\)

D. \(\left( {CC'A} \right).\)

Câu 30. Trong các mệnh đề sau mệnh đề nào sai?

A. Phép chiếu song song biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.

B. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.

C. Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không thay đổi thứ tự của ba điểm đó.

D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.

Câu 31. Phép chiếu song song biến \(\Delta ABC\) thành \(\Delta A'B'C'\) theo thứ tự đó. Vậy phép chiếu song song nói trên, sẽ biến trung điểm \(M\) của cạnh \(BC\) thành

A. Trung điểm \(M'\) của cạnh \(B'C'.\)

B. Trung điểm \(M'\) của cạnh \(A'C'.\)

C. Trung điểm \(M'\) của cạnh \(A'B'.\)

D. Trung điểm \(M'\) của cạnh \(BC.\)

Câu 32. Bảng thống kê sau cho biết tốc độ (km/h) của một số xe máy khi đi qua vị trí có cảnh sát giao thông đang làm nhiệm vụ đo tốc độ trên đường trong khu dân cư, tốc độ tối đa theo quy định là 50 (km/h).

Có bao nhiêu xe vi phạm quy định về an toàn giao thông?

A. \(13.\)

B. \(5.\)

C. \(84.\)

D. \(14.\)

Câu 33. Khảo sát chiều cao của \(40\) học sinh nam ở một trường THPT thu được bảng phân bố tần số ghép nhóm sau:

Giá trị đại diện \({c_3}\) của nhóm chiều cao thứ \(3\) là

A. \({c_3} = 168.\)

B. \({c_3} = 169.\)

C. \({c_3} = 7.\)

D. \({c_3} = 171.\)

Câu 34. Cho mẫu số liệu ghép nhóm về thời gian truy cập Internet mỗi buổi tối của một số học sinh như sau:

Mốt của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào dưới đây?

A. \(19,34.\)

B. \(19,37.\)

C. \(19,43.\)

D. \(24.\)

Câu 35. Cho mẫu số liệu ghép nhóm về thời gian truy cập Internet mỗi buổi tối của một số học sinh như sau:

Tứ phân vị thứ hai của mẫu số liệu ghép nhóm trên là

A. \(15,25.\)

B. \(20.\)

C. \(18,1.\)

D. \(19,34.\)

II. Tự luận (3 điểm)

Bài 1. (1 điểm) Tính giới hạn sau: $\underset{n\to +\infty }{\lim }\left(\sqrt{n^2+3n}-n\right).$

Bài 2. (1 điểm) Cho hình chóp \(S.ABCD\) có đáy là hình bình hành tâm \(O.\) Gọi \(M\) là trung điểm của \(SB,\) \(N\) là điểm trên cạnh \(BC\) sao cho \(BN = 2CN.\)

a) Chứng minh rằng \(OM{\rm{//}}\left( {SCD} \right).\)

b) Xác định giao tuyến của hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {AMN} \right).\)

Bài 3. (0,5 điểm) Gia đình ông An cần khoan một cái giếng. Biết rằng giá của mét khoan đầu tiên là 200 000 đồng và kể từ mét khoan thứ hai, mỗi mét khoan sau sẽ tăng thêm \(6\% \) so với mét khoan trước đó. Hỏi nếu ông An khoan cái giếng sâu 35 m thì hết bao nhiêu tiền (làm tròn đến hàng nghìn).

Bài 4. (0,5 điểm) Cho vận tốc \(v\;\left( {{\rm{cm/s}}} \right)\) của một con lắc đơn theo thời gian \(t\) (giây) được cho bởi công thức $v=-3\sin \left(1,5t+\frac{\pi }{3}\right)$. Xác định các thời điểm \(t\) mà vận tốc con lắc bằng \(1,5\;\left( {{\rm{cm/s}}} \right)\).

ĐÁP ÁN

I. Bảng đáp án trắc nghiệm

Sở Giáo dục và Đào tạo ...

Đề thi Học kì 1 - Chân trời sáng tạo

Năm học ....

Môn: Toán lớp 11

Thời gian làm bài: phút

Đề thi Học kì 1 Toán 11 Chân trời sáng tạo - (Đề số 2)

I. Trắc nghiệm (7 điểm)

Câu 1. Cho góc hình học uOv có số đo 50°. Xác định số đo của góc lượng giác (Ou, Ov) trong hình dưới đây?

A. 50°.

B. 330°.

C. -50°.

D. 130°.

Câu 2. Cho góc $\alpha$ thỏa mãn $\cos \alpha =\frac{3}{5}$. Giá trị của $P=\cos 2\alpha$ là

A. $P=-\frac{2}{5}$.

B. $P=-\frac{7}{25}$.

C. $P=\frac{16}{25}$.

D. $P=\frac{4}{5}$.

Câu 3. Trong các hàm số sau, hàm số nào là hàm số chẵn?

A. y = sin 2x.

B. y = cos x.

C. y = tan 3x.

D. y = 2 cot x.

Câu 4. Tập xác định D của hàm số y = 2 tan x là

A. $D=ℝ$.

B. $D=ℝ\backslash \left(0\right)$.

C. $D=ℝ\backslash \left(\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right)$.

D. $D=ℝ\backslash \left(k\pi ,k\in \mathbb{Z}\right)$.

Câu 5. Nghiệm của phương trình cos 2x = 1 là

A. $x=k\pi ,k\in \mathbb{Z}$.

B. $x=\frac{k\pi }{2},k\in \mathbb{Z}$.

C. $x=\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$.

D. $x=-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}$.

Câu 6. Có bao nhiêu giá trị nguyên của m để phương trình $\sin x-2m=1$ có nghiệm?

A. 3.

B. 2.

C. 1.

D. 0.

Câu 7. Trong các dãy số sau dãy số nào là dãy số tăng?

A. $4;9;14;19;24$.

B. $9;7;5;3;1;0$.

C. $\frac{1}{2};\frac{2}{5};\frac{3}{7};\frac{4}{9};\frac{5}{12}$.

D. $0;1;2;-3;7$.

Câu 8. Dãy số $-1;1;-1;1;-1;\cdots$ có số hạng tổng quát là công thức nào dưới đây?

A. $u_n={\left(-1\right)}^n$.

B. $u_n=-1$.

C. $u_n=1$.

D. $u_n={\left(-1\right)}^{n+1}$.

Câu 9. Cho dãy số $\left(u_n\right)$, biết $u_n=\frac{2n^2-1}{n^2+3}$. Tìm số hạng $u_5$.

A. $u_5=\frac{1}{4}$.

B. $u_5=\frac{7}{4}$.

C. $u_5=\frac{17}{12}$.

D. $u_5=\frac{71}{39}$.

Câu 10. Trong các dãy số sau, dãy số nào là một cấp số cộng?

A. $u_n=-3n+2$.

B. $u_n=n^2+1$.

C. $u_n=\frac{1}{n^2+n}$.

D. $u_n={2.3}^n$.

Câu 11. Cho cấp số cộng $\left(u_n\right)$ có $u_3=9;u_4=3$. Khi đó công sai là

A. 6.

B. 12.

C. 3.

D. -6.

Câu 12. Cho cấp số cộng $\left(u_n\right)$ có $u_1=-5;d=3$. Mệnh đề nào sau đây đúng?

A. $u_{15}=45$.

B. $u_{13}=31$.

C. $u_{15}=34$.

D. $u_{10}=35$.

Câu 13. Trong các dãy số sau, dãy số nào không phải là một cấp số nhân?

A. $1;1;1;1;\mathrm{...}$.

B. $2;4;8;16;\mathrm{...}$.

C. $\sqrt{2};2;2\sqrt{2};4\sqrt{2};\mathrm{...}$.

D. $1;-\frac{1}{3};\frac{1}{9};-\frac{1}{27};\mathrm{...}$.

Câu 14. Cho dãy số $\left(u_n\right)$ biết $\left(\begin{array}{c}{u}_1=3\\ u_{n+1}=3u_n\end{array}\right),\forall n\in {\mathbb{N}}^{*}$. Tìm số hạng tổng quát của dãy số $\left(u_n\right).$

A. $u_n=3^{n-1}$.

B. $u_n=3^{n+1}$.

C. $u_n=3^n$.

D. $u_n=n^{n-1}$.

Câu 15. Cho hai dãy $\left(u_n\right)$ và $\left(v_n\right)$ thỏa mãn $\underset{n\to +\infty }{\lim }{u}_n=\frac{1}{2}$ và $\underset{n\to +\infty }{\lim }{v}_n=-2$. Giá trị của $\underset{n\to +\infty }{\lim }\left(u_n.v_n\right)$ bằng

A. -1.

B. 1.

C. $-\frac{1}{4}$.

D. $\frac{1}{4}$.

Câu 16. Tính $\underset{n\to +\infty }{\lim }\frac{1}{n^2+1}$.

A. 1.

B. $+\infty$.

C. $-\infty$.

D. 0.

Câu 17. Tính $\underset{n\to +\infty }{\lim }{\left(\frac{-3}{4}\right)}^n$.

A. 1.

B. $+\infty$.

C. $-\infty$.

D. 0.

Câu 18. Cho hàm số $f\left(x\right)$ thỏa mãn $\underset{x\to +\infty }{\lim }f\left(x\right)=2$. Giá trị $\underset{x\to +\infty }{\lim }3f\left(x\right)$ bằng

A. 6.

B. 2.

C. 5.

D. $\frac{3}{2}$.

Câu 19. $\underset{x\to 1^{+}}{\lim }\frac{2x-1}{x-1}$ bằng

A. 1.

B. $+\infty$.

C. $-\infty$.

D. 0.

Câu 20. Hàm số nào sau đây liên tục trên ℝ?

A. $y=\sqrt{x}$.

B. $y=\cot x$.

C. $y=\tan x$.

D. $y=\frac{1}{x^2+1}$.

Câu 21. Hàm số $y=f\left(x\right)$ có đồ thị như hình dưới đây:

Hàm số gián đoạn tại điểm

A. x = 1.

B. x = 3.

C. x = 0.

D. x = 2.

Câu 22. Trong các khẳng định sau, khẳng định nào đúng?

A. Qua 4 điểm phân biệt bất kì có duy nhất một mặt phẳng.

B. Qua 3 điểm phân biệt bất kì có duy nhất một mặt phẳng.

C. Qua 3 điểm không thẳng hàng có duy nhất một mặt phẳng.

D. Qua 2 điểm bất kì có duy nhất một mặt phẳng.

Câu 23. Cho hình chóp tứ giác S.ABCD có đáy là hình bình hành tâm O. Điểm M thuộc cạnh SO (M khác S, O). Trong các mặt phẳng sau, điểm M thuộc mặt phẳng nào?

A. (ABCD).

B. (SBD).

C. (SAB).

D. (SCD).

Câu 24. Cho tứ diện ABCD, vị trí tương đối của hai đường thẳng AC và BD là

A. Cắt nhau.

B. Song song.

C. Chéo nhau.

D. Trùng nhau.

Câu 25. Cho tứ diện ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh AB, AC sao cho $\frac{AM}{AB}=\frac{AN}{AC}$; I, J lần lượt là trung điểm của BD và CD.

Khẳng định nào sau đây đúng?

A. IJ cắt BC.

B. IJ song song MN.

C. IJ và MN là hai đường thẳng chéo nhau.

D. IJ và MN là hai đường thẳng song song hoặc chéo nhau.

Câu 26. Cho đường thẳng a và mặt phẳng (P) không có điểm chung. Kết luận nào sau đây đúng?

A. a cắt (P).

B. a cắt (P) hoặc a chéo (P).

C. $a\text{//}\left(P\right)$.

D. a chứa trong (P).

Câu 27. Cho hình chóp tứ giác S.ABCD. Gọi M, N lần lượt là trung điểm của SA, SC. Đường thẳng MN song song với mặt phẳng nào dưới đây?

A. (ABCD).

B. (SAC).

C. (SAD).

D. (SBD).

Câu 28. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SA, SD, AB. Khẳng định nào sau đây đúng?

A. $\left(MON\right)\text{//}\left(MOP\right)$.

B. $\left(MON\right)\text{//}\left(SBC\right)$.

C. $\left(NOP\right)\text{//}\left(MNP\right)$.

D. $\left(SBD\right)\text{//}\left(MNP\right)$.

Câu 29. Cho hình hộp $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$. Mặt phẳng (BC'D) song song với mặt phẳng nào trong các mặt phẳng sau đây?

A. $\left(A{B}^{\text{'}}{D}^{\text{'}}\right)$.

B. $\left(A^{\text{'}}{C}^{\text{'}}C\right)$.

C. $\left(BD{A}^{\text{'}}\right)$.

D. $\left(BC{A}^{\text{'}}\right)$.

Câu 30. Cho các đường thẳng không song song với phương chiếu. Khẳng định nào sau đây là đúng?

A. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song.

B. Phép chiếu song song có thể biến hai đường thẳng song song thành hai đường thẳng cắt nhau.

C. Phép chiếu song song có thể biến hai đường thẳng song song thành hai đường thẳng chéo nhau.

D. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.

Câu 31. Cho hình lăng trụ tam giác $ABC.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}.$

Hình chiếu của tam giác ACB trên mặt phẳng $\left(A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}\right)$ theo phương CC' là

A. Tam giác $A^{\text{'}}{C}^{\text{'}}{B}^{\text{'}}.$

B. Đoạn thẳng $A^{\text{'}}{B}^{\text{'}}.$

C. Tam giác $A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}.$

D. Đoạn thẳng $A^{\text{'}}{C}^{\text{'}}.$

Câu 32. Bảng xếp loại học lực của học sinh lớp 11A của trường năm học 2022 - 2023, được cho như sau:

Số học sinh của lớp 11A trên là bao nhiêu?

A. 45.

B. 5.

C. 15.

D. 35.

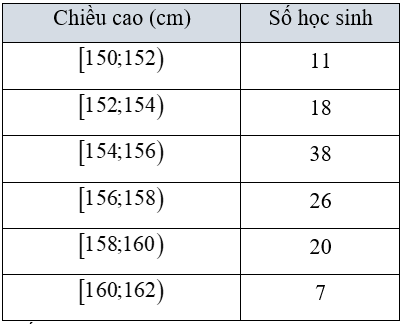
Câu 33. Điều tra về chiều cao của học sinh khối lớp 10 của trường thu được mẫu số liệu ghép nhóm sau:

Nhóm chứa mốt của mẫu số liệu trên là:

A. [150; 152).

B. [160; 162).

C. [154; 156).

D. 38.

Câu 34. Người ta ghi lại tuổi thọ (năm) của bình ắc quy của một hãng xe ô tô cho kết quả như sau:

Trung vị của mẫu số liệu trên thuộc nhóm nào trong các nhóm dưới đây?

A. [2, 5; 3).

B. [3; 3, 5).

C. [3, 5; 4).

D. [4; 4, 5).

Câu 35. Người ta ghi lại tuổi thọ (năm) của 50 bình ắc quy của một hãng xe ô tô của cho kết quả như sau:

Tứ phân vị thứ nhất của mẫu số liệu trên gần với giá trị nào trong các giá trị sau đây?

A. 2,92.

B. 2,97.

C. 2,75.

D. 2,95.

II. Tự luận (3 điểm)

Bài 1. (1 điểm) Tính các giới hạn sau:

a) $\underset{n\to +\infty }{\lim }\left(1+n-n^2\right)$;

b) $\underset{x\to 0}{\lim }\frac{\sqrt{x^2+4}-2}{x}$.

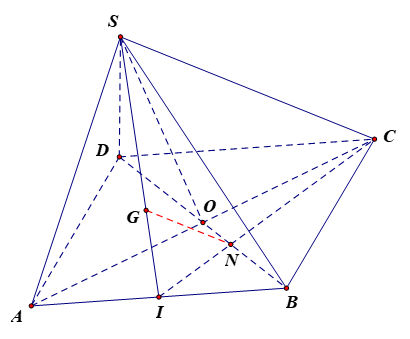
Bài 2. (1 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.

a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).

b) Chứng minh rằng song song với mặt phẳng (SAC).

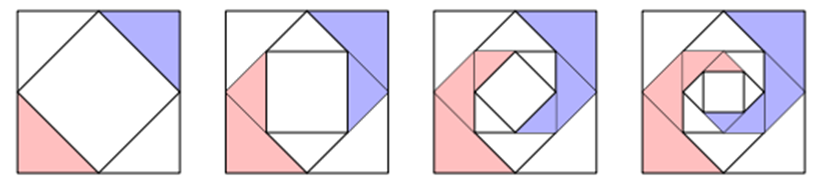
Bài 3. (0,5 điểm) Một thợ thủ công muốn vẽ trang trí một hình vuông kích thước $4\text{m}\times 4\text{m}$ bằng cách vẽ một hình vuông mới với các đỉnh là trung điểm các cạnh của hình vuông ban đầu và tô kín màu lên hai tam giác đối diện (như hình vẽ dưới đây). Quá trình vẽ và tô theo quy luật đó được lặp lại 10 lần. Tính số tiền nước sơn để người thợ đó hoàn thành trang trí hình vuông trên? Biết tiền nước sơn 1 m² là 80 000 đồng.

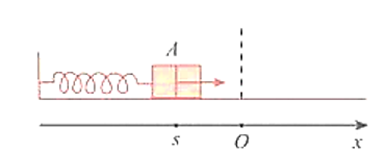
Bài 4. (0,5 điểm) Trong hình sau, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Toạ độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức $s=10\sin \left(10t+\frac{\pi }{2}\right)$. Vào các thời điểm nào thì $s=-5\sqrt{3}\left(\text{cm}\right)$?

(Theo https://www.britannica.com/science/simple-harmonic-motion)

-----HẾT-----

ĐÁP ÁN

I. Bảng đáp án trắc nghiệm

II. Hướng dẫn giải tự luận

Bài 1. (1 điểm) Tính các giới hạn sau:

a) $\underset{n\to +\infty }{\lim }\left(1+n-n^2\right)$;

b) $\underset{x\to 0}{\lim }\frac{\sqrt{x^2+4}-2}{x}$.

Hướng dẫn giải

Bài 2. (1 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.

a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).

b) Chứng minh rằng song song với mặt phẳng (SAC).

Hướng dẫn giải

b) Gọi I là trung điểm của AB.

Vì G là trọng tâm tam giác SAB nên $\frac{IG}{GS}=\frac{1}{2}$.

Vì N là trọng tâm tam giác ABC nên $\frac{IN}{NC}=\frac{1}{2}$.

Xét $\Delta SIC$ có $\frac{IG}{GS}=\frac{IN}{NC}=\frac{1}{2}\Rightarrow GN\text{//}SC$ (Định lý đảo của định lí Thalès).

Khi đó ta có $\left(\begin{array}{c}GN\text{//}SC\\ SC\subset \left(SAC\right)\\ GN\not\subset \left(SAC\right)\end{array}\right)\Rightarrow GN\text{//}\left(SAC\right)$.

Bài 3. (0,5 điểm) Một thợ thủ công muốn vẽ trang trí một hình vuông kích thước $4\text{m}\times 4\text{m}$ bằng cách vẽ một hình vuông mới với các đỉnh là trung điểm các cạnh của hình vuông ban đầu và tô kín màu lên hai tam giác đối diện (như hình vẽ dưới đây). Quá trình vẽ và tô theo quy luật đó được lặp lại 10 lần. Tính số tiền nước sơn để người thợ đó hoàn thành trang trí hình vuông trên? Biết tiền nước sơn 1 m² là 80 000 đồng.

Hướng dẫn giải

Theo quy luật trang trí một hình vuông trên thì ta có các tam giác được tô màu sẽ là tam giác vuông cân.

Gọi $u_n$ là diện tích của hai tam giác được tô màu sau lần vẽ thứ n, với $n\in {\mathbb{N}}^{*}.$

Độ dài cạnh góc vuông của hai tam giác vuông cân được tô màu theo lần vẽ đầu tiên là $\frac{4}{2}=2\left(\text{m}\right)$. Khi đó diện tích của hai tam giác được tô màu sau lần vẽ đầu tiên là

$u_1=2\left(\frac{1}{2}\mathrm{.2.2}\right)=4$ (m²).

Độ dài cạnh góc vuông của hai tam giác vuông cân được tô màu theo lần vẽ thứ hai là $\frac{1}{2}.\sqrt{2^2+2^2}=\sqrt{2}\left(\text{m}\right)$. Khi đó diện tích của hai tam giác được tô màu sau lần vẽ thứ hai là

$u_2=2\left(\frac{1}{2}.\sqrt{2}.\sqrt{2}\right)=4.\frac{1}{2}$ (m²).

Độ dài cạnh góc vuông của hai tam giác vuông cân được tô màu theo lần vẽ thứ ba là $\frac{1}{2}.\sqrt{{\left(\sqrt{2}\right)}^2+{\left(\sqrt{2}\right)}^2}=1\left(\text{m}\right)$. Khi đó diện tích của hai tam giác được tô màu sau lần vẽ thứ ba là

$u_3=2\left(\frac{1}{2}\mathrm{.1.1}\right)=4.{\left(\frac{1}{2}\right)}^2$ (m²).

Khi đó, dãy số $\left(u_n\right)$ là một cấp số nhân với số hạng đầu $u_1=4$ và công bội $q=\frac{1}{2}.$

Ta có công thức số hạng tổng quát $u_n=4.{\left(\frac{1}{2}\right)}^{n-1}$ (m²).

Tổng diện tích của các tam giác được tô màu sau lần vẽ thứ 10 là:

$S_{10}=\frac{4\left(1-{\left(\frac{1}{2}\right)}^{10}\right)}{1-\frac{1}{2}}=\frac{1023}{128}$ (m²).

Vậy số tiền nước sơn là $\frac{1023}{128}.80000=639375$ đồng.

Bài 4. (0,5 điểm) Trong hình sau, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Toạ độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức $s=10\sin \left(10t+\frac{\pi }{2}\right)$. Vào các thời điểm nào thì $s=-5\sqrt{3}\left(\text{cm}\right)$?

(Theo https://www.britannica.com/science/simple-harmonic-motion)

Hướng dẫn giải

-----HẾT-----

................................

................................

................................