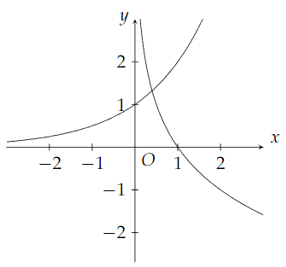Đề cương ôn tập Toán 11 Học kì 2 (Chân trời sáng tạo 2025)
Vietjack.me biên soạn và giới thiệu Đề cương ôn tập Toán 11 Học kì 2 sách Chân trời sáng tạo giúp bạn ôn luyện và đạt kết quả cao trong bài thi Toán 11 Học kì 2.
Đề cương ôn tập Toán 11 Học kì 2 (Chân trời sáng tạo 2025)
Đề cương ôn tập Toán 11 Học kì 2 Chân trời sáng tạo gồm hai phần: Nội dung ôn tập và Bài tập ôn luyện, trong đó:
- 63 bài tập trắc nghiệm;
- 7 bài tập tự luận;
I. NỘI DUNG ÔN TẬP
1. Hàm số mũ và hàm số lôgarit
Bài 1: Phép tính lũy thừa
- Lũy thừa với số mũ nguyên.
- Căn bậc n.
- Lũy thừa với số mũ hữu tỉ.
- Lũy thừa với số mũ thực.
- Tính chất của phép tính lũy thừa.
Bài 2: Phép tính Lôgarit
- Khái niệm về lôgarit.
- Tính lôgarit bằng máy tính cầm tay.
- Các tính chất của lôgarit.
- Công thức đổi cơ số.
Bài 3: Hàm số mũ và hàm số lôgarit
- Hàm số mũ.
- Hàm số lôgarit.
Bài 4: Phương trình và bất phương trình mũ và lôgarit
- Phương trình mũ, phương trình lôgarit.
- Bất phương trình mũ, bất phương trình lôgarit.
2. Đạo hàm
Bài 1: Đạo hàm
- Đạo hàm.
- Ý nghĩa hình học của đạo hàm.
- Số e.
Bài 2: Các quy tắc tính đạo hàm
- Đạo hàm của hàm số y = xn.
- Đạo hàm của hàm số .
- Đạo hàm của hàm số lượng giác.
- Đạo hàm của hàm số mũ và hàm số lôgarit.
- Đạo hàm của tổng, hiệu, tích, thương của hai hàm số.
- Đạo hàm của hàm hợp.
- Đạo hàm cấp hai.
3. Quan hệ vuông góc trong không gian
Bài 1: Hai đường thẳng vuông góc
- Góc giữa hai đường thẳng.
- Hai đường thẳng vuông góc.
Bài 2: Đường thẳng vuông góc với mặt phẳng
- Đường thẳng vuông góc với mặt phẳng.
- Liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng.
- Phép chiếu vuông góc.
Bài 3: Hai mặt phẳng vuông góc
- Góc giữa hai mặt phẳng.
- Hai mặt phẳng vuông góc.
- Tính chất cơ bản về hai mặt phẳng vuông góc.
- Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương.
- Hình chóp đều, hình chóp cụt đều.
Bài 4: Khoảng cách trong không gian
- Khoảng cách từ một điểm đến một đường thẳng, một mặt phẳng.
- Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song.
- Khoảng cách giữa hai đường thẳng chéo nhau.
- Công thức tính thể tích của khối chóp, khối lăng trụ, khối hộp.
Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
- Góc giữa đường thẳng và mặt phẳng.
- Góc nhị diện và góc phẳng nhị diện.
4. Xác suất
Bài 1: Biến cố giao và quy tắc nhân xác suất
- Biến cố giao.
- Hai biến cố xung khắc.
- Biến cố độc lập.
- Quy tắc nhân xác suất của hai biến cố độc lập.
Bài 2: Biến cố hợp và quy tắc cộng xác suất
- Biến cố hợp.
- Quy tắc cộng xác suất.
II. BÀI TẬP ÔN LUYỆN
A. TRẮC NGHIỆM
1. Hàm số mũ và hàm số lôgarit
Bài 1: Phép tính lũy thừa
Bài 1. Giá trị của biểu thức là
A.
B. A = 2;
C. A = 64;
D.
Bài 2. Cho . Khẳng định nào sau đây đúng?
A. a > b;
B. a < b;
C. a b;
D. a b.
Bài 3. Cho biểu thức , trong đó có dạng phân số tối giản. Gọi P = m2 + n2. Khẳng định nào sau đây đúng?
A. P (350; 360);
B. P (360; 370);
C. P (330; 340);
D. P (340; 350).
Bài 4. Cho a là một số thực dương, biểu thức bằng
A. a;
B. a3;
C. a5;
D. 1.
Bài 5. Cho số thực a thỏa mãn a3 > aπ. Mệnh đề nào sau đây đúng?
A. 0 < a < 1;
B. a < 0;
C. a > 1;
D. a = 1.
Bài 2: Phép tính Lôgarit
Bài 1. Giá trị của biểu thức log425 + log21,6 bằng
A. 5;
B. 3;
C. 2;
D. 1.
Bài 2. Cho các số thực a, b dương khác 1 thỏa mãn và . Kết luận nào sau đây đúng?
A. a > 1, b > 1;
B. a > 1, 0 < b < 1;
C. 0 < a < 1, b > 1;
D. 0 < a < 1, 0 < b < 1.
Bài 3. Với a và b là hai số thực dương tùy ý, log(ab2) bằng
A. 2loga + logb;
B. loga + 2logb;
C. 2(loga + logb);
D.
Bài 4. Cho a là một số thực dương khác 1 thỏa mãn Tính loga2.
A.
B. loga2 = 5;
C. loga2 = 20;
D.
Bài 5. Cho log2 = a; log3 = b. Tính log690 theo a, b.
A.
B.
C.
D.
Bài 3: Hàm số mũ và hàm số lôgarit
Bài 1. Tìm tập xác định D của hàm số y = log3(3 – x)
A. D = (3; +∞);
B. D = ℝ\{3};
C. D = ℝ;
D. D = (−∞; 3).
Bài 2. Một người gửi vào ngân hàng 500 triệu đồng với lãi suất 0,6% một tháng, sau mỗi tháng lãi suất được nhập vào vốn. Hỏi sau một năm người đó rút tiền thì tổng số tiền người đó nhận được là bao nhiêu?
A. 500.1,006 triệu đồng;
B. 500.1,0612 triệu đồng;
C. 500.(1 + 12.0,006)12 triệu đồng;
D. 500.1,00612 triệu đồng.
Bài 3. Trong các hàm số sau đây, hàm số nào đồng biến trên ℝ.
A.
B.
C.
D. y = 2-x.
Bài 4. Cho hai đồ thị y = ax và y = logbx có đồ thị như hình vẽ bên. Tìm khẳng định đúng.
A. 0 < a < 1; 0 < b < 1;
B. a > 1; b > 1;
C. a > 1; 0 < b < 1;
D. 0 < a < 1; b > 1.
Bài 5. Trong các hàm số sau, hàm số nào đồng biến trên ℝ.
A. y = log3x;
B.
C.
D. y = 2018x.
Bài 4: Phương trình và bất phương trình mũ và lôgarit
Bài 1. Giải bất phương trình log2(3x – 1) > 3.
A. x > 3;
B.
C. x < 3;
D.
Bài 2. Nghiệm của phương trình 22x – 1 = 2x là
A. x = 2;
B. x = −1;
C. x = 1;
D. x = −2.
Bài 3. Tích các nghiệm của phương trình bằng
A. 5;
B. 0;
C.1;
D. log65.
Bài 4. Phương trình có hai nghiệm x1;x2. Giá trị K = 2x1x2 – 3 bằng
A. 4;
B. 5;
C.6;
D. 7.
Bài 5. Tập nghiệm S của bất phương trình là
A. S = (−∞; 3];
B. S = [3; +∞);
C.S = (−∞; 1];
D. S = [1; +∞).
2. Đạo hàm
Bài 1: Đạo hàm
Bài 1. Cho hàm số f(x) có đạo hàm trên tập số thực. Tìm hệ thức đúng.
A.
B.
C.
D.
Bài 2. Cho hàm số y = f(x) có đạo hàm thỏa mãn f'(6) = 2. Tính giá trị của biểu thức
A. 2;
B.
C.
D. 12.
Bài 3. Tiếp tuyến với đồ thị của hàm số tại điểm có hoành độ x = 2 có hệ số góc là
A.
B.
C. 2;
D. −2.
Bài 4. Cho hàm số có đồ thị (C). Tiếp tuyến của (C) tại điểm có hoành độ x0 = 3 có hệ số góc là
A. 39;
B. 40;
C. 51;
D. 3.
Bài 5. Cho hàm số y = x3 – 3x2 + 4x – 1 có đồ thị là (C). Hệ số góc nhỏ nhất của tiếp tuyến tại một điểm M trên đồ thị (C) là
A. 1;
B. 2;
C. −1;
D. 3.
Bài 2: Các quy tắc tính đạo hàm
Bài 1. Đạo hàm của hàm số y = sinx3 là
A. y' = 3x2cosx2;
B. y' = 3cosx2;
C. y' = 3x2sinx3;
D. y' = 3x2cosx3.
Bài 2. Cho các hàm số u = u(x), v = v(x) có đạo hàm tại mọi x thuộc tập xác định. Khẳng định nào sau đây là sai?
A. (u + v)' = u' + v';
B. (uv)' = u'v + uv';
C. (un)' = nun – 1;
D.
Bài 3. Cho hàm số f(x) = x4 – 3x2 + 5. Tính f'(2)
A. 4;
B. 5;
C. 20;
D. 0.
Bài 4. Hàm số có đạo hàm là
A.
B.
C.
D.
Bài 5. Cho hàm số y = (2x2 + 1)3. Tìm tập hợp tất cả nghiệm của bất phương trình y' 0.
A. ℝ;
B. (−∞; 0];
C. ∅;
D. [0; +∞).
Bài 6. Hàm số có đạo hàm cấp hai tại x = 1 là
A.
B.
C. y"(1) = 4;
D.
Bài 7. Đạo hàm cấp 2 của hàm số y = tanx bằng
A.
B.
C.
D.
Bài 8. Chuyển động của một vật có phương trình với s tính bằng centimét và thời gian t tính bằng giây. Tại các thời điểm vận tốc bằng 0, giá trị tuyệt đối của gia tốc của vật gần giá trị nào sau đây nhất?
A. 4,5 cm/s2;
B. 5,5 cm/s2;
C. 6,3 cm/s2;
D. 7,1 cm/s2.
3. Quan hệ vuông góc trong không gian
Bài 1: Hai đường thẳng vuông góc
Bài 1. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ, CD) bằng
A. 90°;
B. 45°;
C. 30°;
D. 60°.
Bài 2. Cho hình chóp S.ABCD có cạnh SA = x, tất cả các cạnh còn lại đều bằng a. Tính số đo của góc giữa hai đường thẳng SA và SC
A. 90°;
B. 45°;
C. 30°;
D. 60°.
Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA (ABCD), SA = a và M là trung điểm cạnh SD. Côsin góc giữa đường thẳng AC và đường thẳng BM bằng
A.
B.
C.
D.
Bài 4. Chọn khẳng định đúng trong các khẳng định sau
A. Trong không gian hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau;
B. Trong không gian hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau;
C. Trong không gian hai mặt phẳng cùng vuông góc với một đường thẳng thì song song với nhau;
D. Trong không gian hai đường thẳng không có điểm chung thì song song với nhau..
Bài 5. Cho hình chóp S.ABCD có đáy là hình thoi tâm O và SA = SC, SB = SD. Trong các mệnh đề sau mệnh đề nào sai?
A. AC SD;
B. BD AC;
C. BD SA;
D. AC SA.
Bài 2: Đường thẳng vuông góc với mặt phẳng
Bài 1. Cho hai đường thẳng phân biệt a, b và mặt phẳng (α). Mệnh đề nào dưới đây là đúng?
A. Nếu a (α) và b a thì b // (α);
B. Nếu a // (α) và b // (α) thì b // a;
C. Nếu a // (α) và b (α) thì a b;
D. Nếu a // (α) và b a thì b (α).
Bài 2. Cho hình chóp S.ABC có SA (ABC). Gọi H, K lần lượt là trực tâm các tam giác SBC và ABC. Mệnh đề nào sai trong các mệnh đề sau.
A. BC (SAH);
B. HK (SBC);
C. BC (SAB);
D. SH, AK và BC đồng quy.
Bài 3. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA (ABCD). Gọi AE, AF lần lượt là các đường cao của tam giác SAB và tam giác SAD. Khẳng định nào sau đây là đúng?
A. SC (AFB);
B. SC (AEC);
C. SC (AED);
D. SC (AEF).
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Gọi I, J lần lượt là trung điểm của SA và SC. Khẳng định nào dưới đây đúng?
A. IJ AB;
B. IJ AD;
C. IJ BD;
D. IJ SD.
Bài 5. Cho hình hộp ABCD.A'B'C'D' có đáy là hình thoi. Gọi O, O' lần lượt là tâm của hình bình hành ADD'A' và ABB'A'. Trong các mệnh đề sau, mệnh đề nào đúng?
A. OO' AC;
B. OO' AA';
C. OO' AD;
D. OO' AB.
Bài 3: Hai mặt phẳng vuông góc
Bài 1. Cho hình chóp S.ABC có đáy ABC là tam giác đều, cạnh bên SA vuông góc với đáy, M là trung điểm AC, N là hình chiếu của B lên SC. Khẳng định nào sau đây đúng?
A. (BMN) (SBC);
B. (SAC) (SAB);
C. (BMN) (ABC);
D. (SAC) (SBC).
Bài 2. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của SC. Mệnh đề nào sau đây sai?
A. AI SC;
B. (SBC) (SAC);
C. AI BC;
D. (ABI) (SBC).
Bài 3. Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SC = a, . Góc giữa hai mặt phẳng (SAC) và (ABC) bằng
A. 30°;
B. 60°;
C. 45°;
D. 90°.
Bài 4. Cho hình hộp chữ nhật ABCD.A'B'C'D', BC = a, AC = 2a, . Tính góc giữa mặt phẳng (BCD'A') và mặt phẳng (ABCD).
A. 30°;
B. 60°;
C. 45°;
D. 90°.
Bài 5. Cho hình chóp đều S.ABCD có cạnh đáy bằng a, chiều cao bằng 2a. Gọi α là góc giữa mặt phẳng (SAB) và mặt phẳng (ABCD). Tính tanα.
A.
B. tanα = 1;
C. tanα = 4;
D.
Bài 4: Khoảng cách trong không gian
Bài 1. Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 2 và độ dài cạnh bên bằng 3. Khoảng cách từ S đến mặt phẳng (ABCD) bằng
A.
B. 1;
C. 7;
D.
Bài 2. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách từ C đến mặt phẳng (BDB'D') bằng
A.
B.
C.
D.
Bài 3. Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, BC = 2a, SA vuông góc với mặt phẳng đáy và SA = a. Khoảng cách giữa hai đường thẳng AC và SB bằng
A.
B.
C.
D.
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh , cạnh bên và SD vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SB và CD bằng
A.
B.
C. 2a;
D. a.
Bài 5. Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D, SD (ABCD), AD = 2a, . Tính khoảng cách giữa đường thẳng CD và mặt phẳng (SAB).
A.
B.
C.
D.
Bài 6. Hình chóp S.ABCD đáy là hình chữ nhật có ; AD = 2a. Mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABD là
A.
B.
C. 4a3;
D.
Bài 7. Cho tứ diện OABC có OA, OB, OC đôi một vuông góc và OA = OB = OC = a. Khi đó thể tích của tứ diện OABC là
A.
B.
C.
D.
Bài 8. Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, biết AB = a, AC = 2a, A'B = 3a. Tính thể tích của khối lăng trụ ABC.A'B'C'.
A.
B.
C.
D.
Bài 9. Cho hình hộp chữ nhật ABCD.A'B'C'D', biết AB = a, BC = 2a, . Tính thể tích V của khối hộp đó.
A. 4a3;
B. 16a3;
C.
D. 8a3.
Bài 10. Cho khối lăng trụ ABC.A'B'C', tam giác A'BC có diện tích bằng 1 và khoảng cách từ A đến mặt phẳng (A'BC) bằng 2. Thể tích khối lăng trụ đã cho bằng
A. 6;
B. 3;
C. 2;
D. 1.
Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 1. Cho hình chóp S.ABC, cạnh bên SA (ABC). Góc giữa đường thẳng SC và đáy là góc nào dưới đây?
A.
B. hoặc ;
C.
D.
Bài 2. Cho hình chóp tứ giác đều S.ABCD có tất cả cạnh đều bằng a. Góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng
A. 30°;
B. 60°;
C. 45°;
D. α với
Bài 3. Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng 2a, cạnh bên bằng a. Gọi M là trung điểm của BC. Tính góc giữa đường thẳng A'M và mặt phẳng đáy.
A. 30°;
B. 60°;
C. 45°;
D. 90°.
Bài 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy. Góc phẳng nhị diện [S, BC, A] là
A.
B.
C.
D.
Bài 5. Hình chóp đều S.ABCD có tất cả các cạnh bằng a. Tính côsin của góc phẳng nhị diện [S, BC, A]
A.
B.
C.
D.
B. TỰ LUẬN
Bài 1. Tính
a) log400 – log 4.
b)
c) log45.log56.log68.
Bài 2. Biết rằng khi độ cao tăng lên, áp suất không khí sẽ giảm và công thức áp suất dựa trên độ cao là a = 15500.(5 - logp) trong đó a là độ cao so với mực nước biển (tính bằng mét) và p là áp suất không khí (tính bằng pascal). Tính áp suất không khí ở đỉnh Everest có độ cao 8850 m so với mực nước biển.
Bài 3. Vẽ các đồ thị các hàm số sau
a) y = 3x.
b)
Bài 4. Tìm tập xác định của các hàm số sau:
a) y = log|x + 3|.
b) y = 12x.
c) y = log5(2x – 3).
Bài 5. Giải các phương trình sau
a) 2.10x = 30.
b) 42x = 82x – 1.
c) 5x = 32x – 1.
Bài 6. Giải các phương trình sau
a) 2log4x + log2(x – 3) = 2.
b) log3(x2 – 3x + 2) = log3(2x – 4).
Bài 7. Giải các bất phương trình sau
a) 2.52x + 1 3.
b) log3(x + 7) −1.
c) log0,5(x + 7) log0,5(2x – 1).
Xem thêm các chương trình khác:
- TOP 100 Đề thi Toán 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Ngữ văn 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Hóa 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Vật lí 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Sinh học 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Lịch sử 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Địa lí 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Công nghệ 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Tin học 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Kinh tế pháp luật 11 (cả năm) (Kết nối tri thức) năm 2024 - 2025 có đáp án | KTPL
- TOP 100 Đề thi Tiếng Anh 11 (cả năm) (Global success) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Kinh tế pháp luật 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án | KTPL
- TOP 100 Đề thi Tiếng Anh 11 (cả năm) (i-learn Smart World) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Toán 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Ngữ văn 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Vật lí 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Hóa 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Sinh học 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Lịch sử 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Địa lí 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Công nghệ 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án
- TOP 100 Đề thi Tin học 11 (cả năm) (Cánh diều) năm 2024 - 2025 có đáp án