TOP 10 Đề thi Giữa Học kì 1 Toán lớp 6 (Kết nối tri thức) năm 2023 có đáp án

Chỉ từ 150k mua trọn bộ Đề thi Giữa kì 1 Toán lớp 6 Kết nối tri thức bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

TOP 10 Đề thi Giữa Học kì 1 Toán lớp 6 (Kết nối tri thức) năm 2023 có đáp án

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2023 có đáp án  - Đề số 1

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 6

Thời gian làm bài: 60 phút

I. Trắc nghiệm (3 điểm)

Câu 1. Trong các số dưới đây, số nào là số nguyên tố?

A. 1 

B. 57

C. 39

D. 97

Lời giải

Số 1 chỉ có một ước là chính nó nên 1 không phải số nguyên tố.

Số 57 có tổng các chữ số là 5 + 7 = 12 chia hết cho 3 nên 57 chia hết cho 3. Do đó 57 có một ước khác ngoài 1 và chính nó nên 57 là hợp số.

Số 39 có tổng các chữ số là 3 + 9 = 12 chia hết cho 3 nên 39 chia hết cho 3. Do đó 39 có một ước khác ngoài 1 và chính nó nên 39 là hợp số.

Số 97 chỉ có hai ước là 1 và chính nó nên 97 là số nguyên tố.

Chọn D

Câu 2. Cho tập hợp A = {x ∈ N|17 ≤ x ≤ 20} . Tổng các phần tử của tập hợp A là:

A. 74

B. 37

C. 54

D. 44

Lời giải

Các số tự nhiên lớn hơn hoặc bằng 17 và nhỏ hơn 20 gồm: 17; 18; 19.

⇒ A ={17; 18; 19}

Khi đó tổng các phần tử của tập hợp A là: 17 + 18 + 19 = 54.

Chọn C.

Câu 3. Thứ tự thực hiện phép tính nào sau đây là đúng?

A. Lũy thừa – Cộng, trừ – nhân, chia.

B. Cộng, trừ - nhân, chia – Lũy thừa.

C. Cộng, trừ - lũy thừa – nhân, chia.

D. Lũy thừa – Nhân, chia – cộng, trừ.

Lời giải

Thứ tự thực hiện phép tính:

Lũy thừa – Nhân, chia – cộng, trừ.

Chọn D.

Câu 4. Số mũ của kết quả của phép tính sau: 5¹² . 5⁹ : 125

A. 5¹⁸

B. 18

C. 17

D. 5¹⁷

Lời giải

5¹² . 5⁹ : 125 = 5¹²⁺⁹ : 5³ = 5²¹ : 5³ = 5^{21 - 3} = 5¹⁸

Vậy số mũ của kết quả của phép tính là: 18.

Chọn B

Câu 5. Các phát biểu sau đúng hay sai. Đánh dấu X vào ô được lựa chọn

Các phát biểu	Đúng	Sai
1. Số 0 là hợp số
2. 15 chia hết cho 3 và chia hết cho 9
3. Số nguyên biểu diễn cho số La Mã XVI là 16
4. Số chục của số 712 là 12.

Lời giải

Số 0 không phải là hợp số nên phát biểu 1) sai.

15 có tổng các chữ số là 1 + 5 = 6 chia hết cho 3 nhưng không chia hết cho 9 nên 15 chia hết cho 3, không chia hết cho 9. Do đó 2) sai.

Số nguyên biểu diễn cho số La Mã XVI là 16. Do đó 3) đúng.

Số chục của số 712 là: 710. Do đó 4) sai.

Ta có bảng sau: 

Các phát biểu	Đúng	Sai
1. Số 0 là hợp số		X
2. 15 chia hết cho 3 và chia hết cho 9		X
3. Số nguyên biểu diễn cho số La Mã XVI là 16	X
4. Số chục của số 712 là 12.		X

II. Tự luận (7 điểm)
 Bài 1. (2 điểm) Thực hiện phép tính:

a) 37.89 + 37.11;

b) 2⁴ – 2.3²;

c) 250:{5.[88.7897⁰ – (2 024 – 1 946)]};

d) 3.10³ + 2.10² + 0.10 + 5.

Lời giải

 a) 37.89 + 37.11

= 37.(89 + 11)

= 37.100

= 3 700.

b) 3⁴ – 2.3²

= 81 – 2.9

= 81 – 18 

= 63.

c) 250:{5.[88.7897⁰ – (2 024 – 1 946)]}

= 250:{5.[88.1 – 78]}

= 250:{5.10}

= 250:50

= 5.

d) 3.10³ + 2.10² + 0.10 + 5

= 3.1 000 + 2.100 + 0.10 + 5

= 3 205 (Theo cấu tạo số).

Bài 2. (2 điểm) Tìm số tự nhiên x, biết: 

a) x + (120 – 25) = 345;

b) 16.x = 4².4³;

c) 15.(x + 1) + 35 = 2.10²;

d) x ∈ BC và x < 200.

Lời giải

a) x + (120 – 25) = 345 

x + 95 = 345

x         = 345 – 95

x         = 250.

Vậy x = 250.

b) 16.x = 4².4³

16.x = 4^{2 + 3}

16x = 4⁵

x = 4⁵ : 16

x = 4⁵ : 4²

x = 4^{5 – 2} 

x = 4³

x = 64.

Vậy x = 64.

c) 15.(x + 1) + 35 = 2.10²

15(x + 1) + 35 = 200

15(x + 1) = 200 – 35

15(x + 1) = 165

x + 1 = 165:15

x + 1 = 11

x = 11 – 1

x = 10.

Vậy x = 10.

d) Vì 45 = 15.3 nên 45 chia hết cho 15.

Do đó BCNN(15, 45) = 45.

⇒ BC(15;45) = B(45) = {0; 45; 90; 135; 180; 225; ...}

⇒ x ∈ {0; 45; 90; 135; 180; 225; ...}

Mà x < 200 nên x ∈ {0; 45; 90; 135; 180}.

Vậy x ∈ {0; 45; 90; 135; 180}

Bài 3. (2 điểm) Bạn Hoa muốn cắt một tấm bìa hình chữ nhật có kích thước 60cm và 96cm thành các mảnh nhỏ hình vuông sao cho tấm bìa được cắt hết, không thừa không thiếu. Tính độ dài lớn nhất của cạnh hình vuông.

Lời giải

Gọi x là độ dài lớn nhất của cạnh hình vuông 

Vì ta cắt tấm bìa hình chữ nhật có kích thước 60cm, 96cm thành các hình vuông sao cho tấm bìa được cắt hết và không thừa không thiếu nên độ dài cạnh của hình vuông là ước của 60 và 96. Hơn nữa x là lớn nhất nên x chính là ƯCLN(60,96).

Ta có: 60 = 2².3.5, 96 = 2⁵.3

ƯCLN(60,96) = 2².3 = 12.

 x = 12 cm.

Vậy độ dài lớn nhất của hình vuông có thể cắt được là 12cm.

Bài 4. (0,5 điểm) Kết quả của phép tính: 2 021 + 2 022 + 2 023 + 2 024 + 2 025 + 2 026 + 2 027 + 2 028 + 2 029.

Lời giải

2 021 + 2 022 + 2 023 + 2 024 + 2 025 + 2 026 + 2 027 + 2 028 + 2 029

= (2 021 + 2 029) + (2 022 + 2 028) + (2 023 + 2 027) + (2 024 + 2 026) + 2 025

= 4 050 + 4 050 + 4 050 + 4 050 + 2 025

= 16 200 + 2 025

= 18 225.

Bài 5. (0,5 điểm) Cho A = 1 + 3 + 3² + 3³ + … + 3¹⁰¹. Chứng minh rằng A chia hết cho 13

Lời giải

Số các số hạng là: 101 – 0 + 1 = 102 số.

Ta nhận thấy:

1 + 3 + 3² = 1 + 3 + 9 = 13;

3³ + 3⁴ + 3⁵ = 3³(1 + 3 + 3²) = 3³.13;

…

Mà 102 có tổng các chữ số là 1 + 0 + 2 = 3 chia hết cho 3 nên 102 chia hết cho 3, nghĩa là:

A = (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + … + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)

= (1 + 3 + 3²) + 3³(1 + 3 + 3²) + … + 3⁹⁹(1 + 3 + 3²)

= 13 + 3³.13 + … + 3⁹⁹.13

= 13.(1 + 3³ + … + 3⁹⁹) chia hết cho 13.

Vậy A chia hết cho 13.

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2023 có đáp án - Đề số 2

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 6

Thời gian làm bài: 60 phút

I. Trắc nghiệm (2 điểm)

Câu 1. Không làm phép tính hãy cho biết tổng nào sau đây chia hết cho 5?

A. 80 + 1 945 + 15.

B. 1 930 + 100 + 21.

C. 34 + 105 + 20.

D. 1 025 + 2 125 + 46.

Lời giải

Ta có:

+) Vì 80 5; 1 945 5; 15 5 nên 80 + 1 945 + 15 5. Do đó A đúng.

+) Vì 1 930 5; 100 5 và 21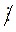 5 nên 1 930 + 100 + 21 không chia hết cho 5. Do đó B sai.

+) Vì 105 5; 20 5 và 34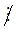 5 nên 34 + 105 + 20 không chia hết cho 5. Do đó C sai.

+) Vì 1 0255; 2 125 5 và 46 5 nên 1 025 + 2 125 + 46 không chia hết cho 5. Do đó D sai.

Chọn A.

Câu 2. Tính 14 + 2.8².

A. 142;                 B. 143;                 C. 144;                 D. 145

Lời giải

14 + 2.8² = 14 + 2.64 = 14 + 128 = 142.

Chọn A. 

Câu 3. Phát biểu dưới đây là sai?

A. 6 là ước của 12.

B. 35 + 14 chia hết cho 7.

C. 121 là bội của 12.

D. 219. 26 + 13 chia hết cho 13.

Lời giải

Ta có 12 chia hết cho 6 nên 6 là ước của 12. Do đó A đúng.

Vì 35 chia hết cho 7 và 14 chia hết cho 7 nên 35 + 14 chia hết cho 7. Do đó B đúng.

121 không chia hết cho 12 nên 121 không là bội của 12. Do đó C sai.

Ta có 219.26 = 219.13.2 chia hết cho 13, 13 cũng chia hết cho 13 nên 219.26 + 13 chia hết cho 13. Do đó D đúng.

Chọn C.

Câu 4: Số La Mã biểu diễn số 29 là?

A. XIX;

B. XXIX;

C. XXXI;

D. XXVIV.

Lời giải

Số La Mã biểu diễn cho số 29 là: XXIX.

Chọn B.

II. Tự luận (7 điểm)

Bài 1. (2 điểm) Thực hiện phép tính:

a) 120 + [55 – (11 – 3.2)²] + 2³;

b) 2³.3 - (1¹⁰ + 15) : 4²;

c) 21.[(1 245 + 987):2³ – 15.12] + 21;

d) 321 – 21.[(2.3³ + 4⁴:32) – 52].

Lời giải

a) 120 + [55 – (11 – 3.2)²] + 2³

= 120 + [55 – (11 – 6)²] + 8

= 120 + [55 – 5²] + 8

= 120 + [55 – 25] + 8

= 120 + 30 + 8 

= 150 + 8 

= 158.

b) 2³.3 - (1¹⁰ + 15) : 4²

= 8.3 - (1 + 15) : 16

= 24 - 16 : 16

= 24 - 1 

= 23.

c) 21.[(1 245 + 987):2³ – 15.12] + 21

= 21.[2 232:8 – 180] + 21

= 21.[279 – 180] + 21

= 21.99 + 21

= 21(99 + 1)

= 21.100

= 2 100.

d) 321 – 21.[(2.3³ + 4⁴:32) – 52].

= 321 – 21[2.27 + 64:32) – 52]

= 321 – 21[54 + 2 – 52]

= 321 – 21.4

= 321 – 84 

= 237.

Bài 2. (2 điểm) Tìm giá trị của x thỏa mãn: 

a) 3(5x – 15) – 52 = 68;

b) {2³ + [1 + (3 – 1)²]}:x = 13;

c) 32 < 2^x ≤ 512;

d) Thay x trong số 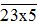  bằng chữ số thích hợp để số đó chia hết cho 9.

Lời giải

a) 3(5x – 15) – 52 = 68

3(5x – 15) = 68 + 52

3(5x – 15) = 120

5x – 15 = 120:3

5x – 15 = 40

5x = 40 + 15

5x = 55

x = 55:5

x = 11.

Vậy x = 11.

b) {2³ + [1 + (3 – 1)²]}:x = 13

{8 + [1 + 2²]}:x = 13

{8 + [1 + 4]}:x = 13

{8 + 5}:x = 13

13:x = 13

x = 13:13

x = 1.

Vậy x = 1. 

c) Ta có: 32 < 2^x ≤ 512

Mà 32 = 2.2.2.2.2 = 2⁵; 512 = 2.2.2.2.2.2.2.2.2 = 2⁹.

Nghĩa là 2⁵ < 2^x ≤ 2⁹.

Khi đó: 5 < x ≤ 9, mà x là số tự nhiên nên x ∈ {6; 7; 8; 9}.

Vậy x ∈ {6; 7; 8; 9}.

d) Ta có 2 + 3 + x + 5 = 10 + x.

Để số đã cho chia hết cho 9 thì 10 + x phải chia hết cho 9.

Nên x thuộc {8; 17; 26; …}.

Mà x là chữ số nên x = 8.

Vậy x = 8.

Bài 3. (2 điểm) Trong một buổi tập đồng diễn thể dục có khoảng 400 đến 500 người tham gia. Thầy tổng phụ trách cho xếp thành hàng 5, hàng 6 và hàng 8 thì đều thừa một người. Hỏi có chính xác bao nhiêu người dự buổi tập đồng diễn thể dục.

Lời giải

Gọi số người tham gia buổi tập đồng diễn thể dục là x (x ∈ N, 400 < x < 500).

Do số người tham gia xếp thàng hàng 5, hàng 6 và hàng 8 đều thừa một người nên ta có:

x – 1 5

x – 16

x – 18

nên x – 1 ∈ BC(5, 6, 8).

Ta có 5 = 5, 6 = 2.3, 8 = 2³.

Khi đó: BCNN(5, 6, 8) = 2³.3.5 = 8.3.5 = 120.

Suy ra BC(5, 6, 8) = B(120) = {0; 120; 240; 360; 480; 600; …}.

Do đó x – 1 ∈ {0; 120; 240; 360; 480; 600; …}.

Hay x ∈ {1; 121; 241; 361; 481; 601; …}.

Mà 400 < x < 500 nên x = 481. 

Bài 4. (1 điểm) Trong một phép chia, số bị chia là 89, số dư là 12. Tìm số chia và thương.

Lời giải

Gọi số chia và thương lần lượt là b và q (b; q ∈ N, b ≠0).

Như vậy 89 : b = q (dư 12) và b > 12 (số chia lớn hơn số dư).

Từ đó 89 = bq + 12. Suy ra bq = 89 – 12 = 77 = 7 . 11 = 77 . 1

Mà b > 12 nên b = 77 và q = 1.

Do đó 89 : 77 = 1 (dư 12).

Vậy số chia bằng 77, thương bằng 1.

Bài 5. (1 điểm) Gọi A = n² + n + 1 (với n ∈ N). Chứng tỏ rằng A không chia hết cho 4.

Lời giải

Ta có: A = n² + n + 1 = n(n+1)+1

Vì n ∈ N nên n + 1 ∈ N. 

Nếu n là số chẵn thì n(n + 1) chia hết cho 2.

Nếu n là số lẻ thì n + 1 là số chẵn nên n(n + 1) chia hết cho 2.

Do đó n(n + 1) chia hết cho 2 với mọi số tự nhiên n.

Mà 1 không chia hết cho 2 nên n(n+1) + 1 không chia hết cho 2.

Suy ra n(n + 1) + 1 không chia hết cho 2 với mọi số tự nhiên n.

Vậy A không chia hết cho 4 với mọi số tự nhiên n.

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2023 có đáp án - Đề số 3

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 76

Thời gian làm bài: 60 phút

I. Trắc nghiệm (2 điểm)

Câu 1. Cho tập hợp A = {chó, mèo, lợn, gà}. Phát biểu nào dưới đây là đúng?

A. Chó ∈ A;

B. Mèo ∉ A;

C. Cá ∈ A;

D. Lợn ∉ A.

Lời giải

Ta có:

Chó là một phần tử của tập hợp A nên ta viết chó ∈ A. Do đó A đúng.

Mèo là một phần tử của tập hợp A nên ta viết mèo ∈ A. Do đó B sai.

Cá không phải là phần tử của tập hợp A nên ta viết cá ∉ A. Do đó C sai.

Lợn là một phần tử của tập hợp A nên ta viết lợn ∈ A. Do đó D sai.

Chọn A.

Câu 2. Chữ số 2 trong số 123 857 có giá trị là:

A. 120 000

B. 20 000

C. 23 857

D. 20

Lời giải

Trong số 123 857, chữ số 2 là chữ số hàng chục nghìn nên chữ số 2 có giá trị 2.10 000 = 20 000.

Chọn B.

Câu 3. Trong các số sau: 114, 76; 1 029; 354; 57. Có bao nhiêu số chia hết cho 3?

A. 3

B. 0

C. 5

D. 4

Lời giải

Ta có:

1 + 1 + 4 = 6 chia hết cho 3 nên 114 chia hết cho 3;

7 + 6 = 13 không chia hết cho 3 nên 76 không chia hết cho 3;

1 + 0 + 2 + 9 = 12 chia hết cho 3 nên 1 029 chia hết cho 3;

3 + 5 + 4 = 12 chia hết cho 3 nên 354 chia hết cho 3;

5 + 7 = 12 chia hết cho 3 nên 57 chia hết cho 3.

Vậy có 4 số chia hết cho 3.

Chọn D

Câu 4. Kết quả của phép tính sau: 7⁸ : 7

A. 7⁸;

B. 7⁶;

C. 7⁷;

D. 7⁹.

Lời giải

Ta có: 7⁸ : 7 = 7^{8 – 1} = 7⁷.

Chọn C.

II. Tự luận (8 điểm)

Bài 1. (2 điểm) Thực hiện phép tính:

a) 12 + 3.2⁵ : 4 – 3;

b) 120 + [55 – (11 – 3.2)²] + 2³;

c) 24⁰.14.83 + 7.2.17.

Lời giải

a) 12 + 3.2⁵ : 4 – 3

= 12 + 3.32:4 – 3

= 12 + 3.8 – 4

= 12 + 24 – 4

= 36 – 4

= 32

b) 120 + [55 – (11 – 3.2)²] + 2³

= 120 + [55 – (11 – 6)²] + 8

= 120 + [55 – 4²] + 8

= 120 + [55 – 16] + 8

= 120 + 39 + 8

= 159 + 8

= 167

c) 24⁰.14.83 + 7.2.17

= 14.83 + 14.17

= 14.(83 + 17)

= 14.100

= 1 400.

Bài 2. (2 điểm) Tìm x, biết:

a) 2x + 15 = 242:2;

b) (3x – 4)³ = 125;

c) x ∈ ƯC(18,54) và x > 6.

Lời giải

a) 2x + 15 = 242:2

2x + 15 = 121

2x = 121 – 15

2x = 106

x = 106 : 2

x = 53.

Vậy x = 53.

b) (3x – 4)³ = 125

(3x – 4)³ = 5³

3x – 4 = 5

3x = 5 + 4

3x = 9

x = 9:3

x = 3.

Vậy x = 3.

c) x ƯC(18,54) và x > 6

Ta có: 18 = 2.3², 54 = 2.3³

Khi đó: ƯCLN(18, 54) = 2.3² = 18.

ƯC(18,54) = Ư(18) = {1; 2; 3; 6; 9; 18}

x ∈ {1; 2; 3; 6; 9; 18}

Mà x > 6 nên x ∈ {9; 18}.

Vậy x ∈ {9; 18}.

Bài 3. (1 điểm) Cho tập hợp A là tập hợp các số tự nhiên chia hết cho 2 và 5, lớn hơn 12 nhỏ hơn hoặc bằng 70. Hãy viết tập hợp A theo hai cách.

Lời giải

Các số tự nhiên chia hết cho 2 và cho 5 là các số tự nhiên có chữ số tận cùng bằng 0: 0; 10; 20; 30; 40; 50; 60; 70; 80; …

Các số tự nhiên ở trên thỏa mãn lớn hơn 12 nhỏ hơn hoặc bằng 70 là: 20; 30; 40; 50; 60; 70.

Theo cách liệt kê, tập hợp A được mô tả: A = {20; 30; 40; 50; 60; 70}.

Theo cách chỉ ra tính chất đặc trưng, ta viết: {x ∈ N|x2, x5, 12 < x ≤ 70}

Bài 4. (1,5 điểm) Tuấn và Hà mỗi người mua một số hộp bút chì màu, trong mỗi hộp đều có từ hai chiếc bút trở lên và số bút trong mỗi hộp là như nhau. Tính ra Tuấn mua 25 bút, Hà mua 20 bút. Hỏi mỗi hộp bút chì màu có bao nhiêu chiếc?

Lời giải

Gọi số bút trong mỗi hộp bút chì màu là x ( x ∈ N, x > 2) (chiếc).

Vì số bút trong mỗi hộp là như nhau nên 25 và 20 chia hết cho x hay x ƯC(25, 20).

Ta có: 25 = 5², 20 = 2².5;

ƯCLN(25, 20) = 5.

ƯC(25, 20) = Ư(5) = {1; 5}

x ∈ {1; 5}

Mà x > 2 nên x = 5 (thỏa mãn điều kiện).

Vậy trong mỗi hộp có 5 chiếc bút.

Bài 5. (0,5 điểm) Tìm số tự nhiên có hai chữ số biết số đó chia cho tổng các chữ số của nó thu được 7 dư 6.

Lời giải

Gọi số tự nhiên có hai chữ số cần tìm là 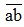 (Với a,b {0;1;2;3; …; 9} và a ≠ 0 )

Ta có tổng các chữ số của nó là: a + b.

Vì số dư phép chia là 6 nên a + b > 6.

Theo đầu bài ta có: 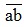 = 7(a + b) + 6

10a + b = 7a + 7b + 6

3a = 6b + 6

a = 2b + 2

a = 2(b + 1)

Mà 0 < a ≤ 9 ⇔ 0 < 2(b + 1) ≤ 9 ⇒ 0 < b + 1 < 4,5.

Do đó 0 ≤ b < 5.

Ta có bảng sau:

 

Vậy số cần tìm là 62 và 83.

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2023 có đáp án - Đề số 4

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 6

Thời gian làm bài: 90 phút

I. TRẮC NGHIỆM: (3,0 điểm)

Khoanh tròn vào chữ cái đứng trước câu trả lời đúng trong mỗi câu sau:

Câu 1. Cho tập hợp A = {a; b; c; d}, khẳng định nào sau đây là đúng?

A. c ∈ A
B. d ∈ A
C. e ∈ A
D. a ∉ A

Câu 2. Tập hợp nào sau đây chỉ gồm các phần tử là số tự nhiên?

A. 
B. {1; 2; 3}
C. 
D. {0; 2; 4}

Câu 3. Với a, m, n là các số tự nhiên, khẳng định nào sau đây đúng?

A. a^m . aⁿ = a^m + n (a ≠ 0)
B. a^m . aⁿ = a^m.n (a ≠ 0)
C. a^m : aⁿ = a^m.n (a ≠ 0)
D. a^m : aⁿ = m – n (a ≠ 0)

Câu 4. Thứ tự thực hiện các phép tính trong biểu thức không chứa dấu ngoặc là:

A. Lũy thừa → Nhân, chia → Cộng, trừ.
B. Nhân chia → Cộng trừ → Lũy thừa.
C. Nhân chia → Lũy thừa → Cộng, trừ.
D. Cộng, trừ → Nhân, chia → Lũy thừa.

Câu 5. Kết quả của phép tính 2³. 2² là:

A. 4⁵
B. 2⁵
C. 2⁶
D. 4⁶

Câu 6. Số tự nhiên nào sau đây chia cho 5 dư 2?

A. 4
B. 5
C. 6
D. 7

Câu 7. Số tự nhiên nào sau đây chia hết cho cả 2 và 5?

A. 126
B. 259
C. 430
D. 305

Câu 8. Trong các số tự nhiên sau, số nào là số nguyên tố?

A. 4
B. 7
C. 18
D. 25

Câu 9. Số tự nhiên nào sau đây là ước của 10?

A. 0
B. 3
C. 2
D. 11

Câu 10. Số tự nhiên nào sau đây là BCNN(4, 6)?

A. 15
B. 12
C. 10
D. 9

Câu 11. Khi mô tả các yếu tố của hình vuông, khẳng định nào sau đây sai:

A. Hình vuông có 4 cạnh bằng nhau;
B. Hình vuông có 4 góc vuông;
C. Hình vuông có các cạnh đối không bằng nhau;
D. Hình vuông có hai đường chéo bằng nhau.

Câu 12. Hình nào sau đây là hình chữ nhật?

II. TỰ LUẬN: (7,0 điểm)

Câu 1. (1,0 điểm) Trong hình vẽ bên có bao nhiêu tam giác đều? Hãy viết tên các tam giác đều đó.

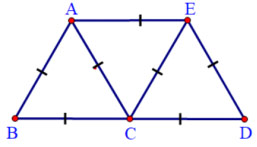
Câu 2. (2,0 điểm)

a) Viết tập hợp A các số tự nhiên không vượt quá 7.

b) Viết các số 23 và 29 bằng số La Mã.

Câu 3. (1,5 điểm)

a) Thực hiện phép tính: ( tính hợp lý nếu có thể) 12. 35 + 12. 65

b) Tìm x, biết: (123 - 4x) - 67 = 2³

Câu 4. (1,5 điểm)

a) Tìm tập hợp BC (30; 45)

b) Một đội y tế có 24 bác sĩ và 108 y tá. Có thế chia đội y tế đó nhiều nhất thành mấy tổ để số y tá được chia đều vào các tổ ?

Câu 5. (1,0 điểm) Tìm n ∈ N biết để 3 chia hết cho n + 2.

Đáp án đề thi giữa kì 1 môn Toán 6 năm 2023

I. TRẮC NGHIỆM (3,0 điểm) Mỗi câu trả lời đúng: 0,25 điểm

 

II. TỰ LUẬN ( 7,0 điểm)

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2023 có đáp án - Đề số 5

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 6

Thời gian làm bài: 60 phút

A. Phần đề bài

I. Trắc nghiệm (3 điểm)

Câu 1. Trong các số dưới đây, số nào là số nguyên tố?

A. 1 

B. 57

C. 39

D. 97

Câu 2. Cho tập hợp A = {x ∈ N|17 ≤ x ≤ 20} . Tổng các phần tử của tập hợp A là:

A. 74

B. 37

C. 54

D. 44

Câu 3. Thứ tự thực hiện phép tính nào sau đây là đúng?

A. Lũy thừa – Cộng, trừ – nhân, chia.

B. Cộng, trừ - nhân, chia – Lũy thừa.

C. Cộng, trừ - lũy thừa – nhân, chia.

D. Lũy thừa – Nhân, chia – cộng, trừ.

Câu 4. Số mũ của kết quả của phép tính sau: 5¹² . 5⁹ : 125

A. 5¹⁸

B. 18

C. 17

D. 5¹⁷

Câu 5. Các phát biểu sau đúng hay sai. Đánh dấu X vào ô được lựa chọn

Các phát biểu	Đúng	Sai
1. Số 0 là hợp số
2. 15 chia hết cho 3 và chia hết cho 9
3. Số nguyên biểu diễn cho số La Mã XVI là 16
4. Số chục của số 712 là 12.

II. Tự luận (7 điểm)
 Bài 1. (2 điểm) Thực hiện phép tính:

a) 37.89 + 37.11;

b) 2⁴ – 2.3²;

c) 250:{5.[88.7897⁰ – (2 024 – 1 946)]};

d) 3.10³ + 2.10² + 0.10 + 5.

Bài 2. (2 điểm) Tìm số tự nhiên x, biết: 

a) x + (120 – 25) = 345;

b) 16.x = 4².4³;

c) 15.(x + 1) + 35 = 2.10²;

d) x ∈ BC và x < 200.

Bài 3. (2 điểm) Bạn Hoa muốn cắt một tấm bìa hình chữ nhật có kích thước 60cm và 96cm thành các mảnh nhỏ hình vuông sao cho tấm bìa được cắt hết, không thừa không thiếu. Tính độ dài lớn nhất của cạnh hình vuông.

Bài 4. (0,5 điểm) Kết quả của phép tính: 2 021 + 2 022 + 2 023 + 2 024 + 2 025 + 2 026 + 2 027 + 2 028 + 2 029.

Bài 5. (0,5 điểm) Cho A = 1 + 3 + 3² + 3³ + … + 3¹⁰¹. Chứng minh rằng A chia hết cho 13

B. Đán án và lời giải  

I. Phần trắc nghiệm

Câu 1: D

Câu 2: C

Câu 3: D

Câu 4: B

Câu 1:

Số 1 chỉ có một ước là chính nó nên 1 không phải số nguyên tố.

Số 57 có tổng các chữ số là 5 + 7 = 12 chia hết cho 3 nên 57 chia hết cho 3. Do đó 57 có một ước khác ngoài 1 và chính nó nên 57 là hợp số.

Số 39 có tổng các chữ số là 3 + 9 = 12 chia hết cho 3 nên 39 chia hết cho 3. Do đó 39 có một ước khác ngoài 1 và chính nó nên 39 là hợp số.

Số 97 chỉ có hai ước là 1 và chính nó nên 97 là số nguyên tố.

Chọn D

Câu 2:

Các số tự nhiên lớn hơn hoặc bằng 17 và nhỏ hơn 20 gồm: 17; 18; 19.

⇒ A ={17; 18; 19}

Khi đó tổng các phần tử của tập hợp A là: 17 + 18 + 19 = 54.

Chọn C.

Câu 3:

Thứ tự thực hiện phép tính:

Lũy thừa – Nhân, chia – cộng, trừ.

Chọn D.

Câu 4:

5¹² . 5⁹ : 125 = 5¹²⁺⁹ : 5³ = 5²¹ : 5³ = 5^{21 - 3} = 5¹⁸

Vậy số mũ của kết quả của phép tính là: 18.

Chọn B

Câu 5:

Số 0 không phải là hợp số nên phát biểu 1) sai.

15 có tổng các chữ số là 1 + 5 = 6 chia hết cho 3 nhưng không chia hết cho 9 nên 15 chia hết cho 3, không chia hết cho 9. Do đó 2) sai.

Số nguyên biểu diễn cho số La Mã XVI là 16. Do đó 3) đúng.

Số chục của số 712 là: 710. Do đó 4) sai.

Ta có bảng sau: 

Các phát biểu	Đúng	Sai
1. Số 0 là hợp số		X
2. 15 chia hết cho 3 và chia hết cho 9		X
3. Số nguyên biểu diễn cho số La Mã XVI là 16	X
4. Số chục của số 712 là 12.		X

 II. Phần tự luận

Câu 1:

 a) 37.89 + 37.11

= 37.(89 + 11)

= 37.100

= 3 700.

b) 3⁴ – 2.3²

= 81 – 2.9

= 81 – 18 

= 63.

c) 250:{5.[88.7897⁰ – (2 024 – 1 946)]}

= 250:{5.[88.1 – 78]}

= 250:{5.10}

= 250:50

= 5.

d) 3.10³ + 2.10² + 0.10 + 5

= 3.1 000 + 2.100 + 0.10 + 5

= 3 205 (Theo cấu tạo số).

Câu 2:

a) x + (120 – 25) = 345 

x + 95 = 345

x         = 345 – 95

x         = 250.

Vậy x = 250.

b) 16.x = 4².4³

16.x = 4^{2 + 3}

16x = 4⁵

x = 4⁵ : 16

x = 4⁵ : 4²

x = 4^{5 – 2} 

x = 4³

x = 64.

Vậy x = 64.

c) 15.(x + 1) + 35 = 2.10²

15(x + 1) + 35 = 200

15(x + 1) = 200 – 35

15(x + 1) = 165

x + 1 = 165:15

x + 1 = 11

x = 11 – 1

x = 10.

Vậy x = 10.

d) Vì 45 = 15.3 nên 45 chia hết cho 15.

Do đó BCNN(15, 45) = 45.

⇒ BC(15;45) = B(45) = {0; 45; 90; 135; 180; 225; ...}

⇒ x ∈ {0; 45; 90; 135; 180; 225; ...}

Mà x < 200 nên x ∈ {0; 45; 90; 135; 180}.

Vậy x ∈ {0; 45; 90; 135; 180}

Câu 3:

Gọi x là độ dài lớn nhất của cạnh hình vuông 

Vì ta cắt tấm bìa hình chữ nhật có kích thước 60cm, 96cm thành các hình vuông sao cho tấm bìa được cắt hết và không thừa không thiếu nên độ dài cạnh của hình vuông là ước của 60 và 96. Hơn nữa x là lớn nhất nên x chính là ƯCLN(60,96).

Ta có: 60 = 2².3.5, 96 = 2⁵.3

ƯCLN(60,96) = 2².3 = 12.

 x = 12 cm.

Vậy độ dài lớn nhất của hình vuông có thể cắt được là 12cm.

Câu 4:

2 021 + 2 022 + 2 023 + 2 024 + 2 025 + 2 026 + 2 027 + 2 028 + 2 029

= (2 021 + 2 029) + (2 022 + 2 028) + (2 023 + 2 027) + (2 024 + 2 026) + 2 025

= 4 050 + 4 050 + 4 050 + 4 050 + 2 025

= 16 200 + 2 025

= 18 225.

Câu 5:

Số các số hạng là: 101 – 0 + 1 = 102 số.

Ta nhận thấy:

1 + 3 + 3² = 1 + 3 + 9 = 13;

3³ + 3⁴ + 3⁵ = 3³(1 + 3 + 3²) = 3³.13;

…

Mà 102 có tổng các chữ số là 1 + 0 + 2 = 3 chia hết cho 3 nên 102 chia hết cho 3, nghĩa là:

A = (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + … + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)

= (1 + 3 + 3²) + 3³(1 + 3 + 3²) + … + 3⁹⁹(1 + 3 + 3²)

= 13 + 3³.13 + … + 3⁹⁹.13

= 13.(1 + 3³ + … + 3⁹⁹) chia hết cho 13.

Vậy A chia hết cho 13.

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2023 có đáp án - Đề số 6

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 6

Thời gian làm bài: .........

A. Phần đề bài

I. Trắc nghiệm (2 điểm)

Câu 1. Không làm phép tính hãy cho biết tổng nào sau đây chia hết cho 5?

A. 80 + 1 945 + 15.

B. 1 930 + 100 + 21.

C. 34 + 105 + 20.

D. 1 025 + 2 125 + 46.

Câu 2. Tính 14 + 2.8².

A. 142;                 B. 143;                 C. 144;                 D. 145

Câu 3. Phát biểu dưới đây là sai?

A. 6 là ước của 12.

B. 35 + 14 chia hết cho 7.

C. 121 là bội của 12.

D. 219. 26 + 13 chia hết cho 13.

Câu 4: Số La Mã biểu diễn số 29 là?

A. XIX;

B. XXIX;

C. XXXI;

D. XXVIV

II. Tự luận (7 điểm)

Bài 1. (2 điểm) Thực hiện phép tính:

a) 120 + [55 – (11 – 3.2)²] + 2³;

b) 2³.3 - (1¹⁰ + 15) : 4²;

c) 21.[(1 245 + 987):2³ – 15.12] + 21;

d) 321 – 21.[(2.3³ + 4⁴:32) – 52].

Bài 2. (2 điểm) Tìm giá trị của x thỏa mãn: 

a) 3(5x – 15) – 52 = 68;

b) {2³ + [1 + (3 – 1)²]}:x = 13;

c) 32 < 2^x ≤ 512;

d) Thay x trong số    bằng chữ số thích hợp để số đó chia hết cho 9.

Bài 3. (2 điểm) Trong một buổi tập đồng diễn thể dục có khoảng 400 đến 500 người tham gia. Thầy tổng phụ trách cho xếp thành hàng 5, hàng 6 và hàng 8 thì đều thừa một người. Hỏi có chính xác bao nhiêu người dự buổi tập đồng diễn thể dục.

Bài 4. (1 điểm) Trong một phép chia, số bị chia là 89, số dư là 12. Tìm số chia và thương.

Bài 5. (1 điểm) Gọi A = n² + n + 1 (với n ∈ N). Chứng tỏ rằng A không chia hết cho 4.

B. Phần đáp án và lời giải

Phần I. Trắc nghiệm

Bảng đáp án (0,5 × 4 = 2 điểm)

Câu 1: A

Câu 2: A

Câu 3: C

Câu 4: B

Hướng dẫn chi tiết:

Câu 1:

Ta có:

+) Vì 80 $⋮$5; 1 945 $⋮$ 5; 15 $⋮$ 5 nên 80 + 1 945 + 15 $⋮$ 5. Do đó A đúng.

+) Vì 1 930 $⋮$ 5; 100 $⋮$ 5 và 21 $\cancel{⋮}$ 5 nên 1 930 + 100 + 21 không chia hết cho 5. Do đó B sai.

+) Vì 105 $⋮$ 5; 20 $⋮$ 5 và 34 $\cancel{⋮}$ 5 nên 34 + 105 + 20 không chia hết cho 5. Do đó C sai.

+) Vì 1 025 $⋮$ 5; 2 125 $⋮$ 5 và 46 $\cancel{⋮}$ 5 nên 1 025 + 2 125 + 46 không chia hết cho 5. Do đó D sai.

Chọn A.

Câu 2:

14 + 2.8² = 14 + 2.64 = 14 + 128 = 142.

Chọn A. 

Câu 3:

Ta có 12 chia hết cho 6 nên 6 là ước của 12. Do đó A đúng.

Vì 35 chia hết cho 7 và 14 chia hết cho 7 nên 35 + 14 chia hết cho 7. Do đó B đúng.

121 không chia hết cho 12 nên 121 không là bội của 12. Do đó C sai.

Ta có 219.26 = 219.13.2 chia hết cho 13, 13 cũng chia hết cho 13 nên 219.26 + 13 chia hết cho 13. Do đó D đúng.

Chọn C.

Câu 4:

Số La Mã biểu diễn cho số 29 là: XXIX.

Chọn B.

Phần II. Tự luận

Câu 1:

a) 120 + [55 – (11 – 3.2)²] + 2³

= 120 + [55 – (11 – 6)²] + 8

= 120 + [55 – 5²] + 8

= 120 + [55 – 25] + 8

= 120 + 30 + 8 

= 150 + 8 

= 158.

b) 2³.3 - (1¹⁰ + 15) : 4²

= 8.3 - (1 + 15) : 16

= 24 - 16 : 16

= 24 - 1 

= 23.

c) 21.[(1 245 + 987):2³ – 15.12] + 21

= 21.[2 232:8 – 180] + 21

= 21.[279 – 180] + 21

= 21.99 + 21

= 21(99 + 1)

= 21.100

= 2 100.

d) 321 – 21.[(2.3³ + 4⁴:32) – 52].

= 321 – 21[2.27 + 64:32) – 52]

= 321 – 21[54 + 2 – 52]

= 321 – 21.4

= 321 – 84 

= 237.

Câu 2:

a) 3(5x – 15) – 52 = 68

3(5x – 15) = 68 + 52

3(5x – 15) = 120

5x – 15 = 120:3

5x – 15 = 40

5x = 40 + 15

5x = 55

x = 55:5

x = 11.

Vậy x = 11.

b) {2³ + [1 + (3 – 1)²]}:x = 13

{8 + [1 + 2²]}:x = 13

{8 + [1 + 4]}:x = 13

{8 + 5}:x = 13

13:x = 13

x = 13:13

x = 1.

Vậy x = 1. 

c) Ta có: 32 < 2^x ≤ 512

Mà 32 = 2.2.2.2.2 = 2⁵; 512 = 2.2.2.2.2.2.2.2.2 = 2⁹.

Nghĩa là 2⁵ < 2^x ≤ 2⁹.

Khi đó: 5 < x ≤ 9, mà x là số tự nhiên nên x ∈ {6; 7; 8; 9}.

Vậy x ∈ {6; 7; 8; 9}.

d) Ta có 2 + 3 + x + 5 = 10 + x.

Để số đã cho chia hết cho 9 thì 10 + x phải chia hết cho 9.

Nên x thuộc {8; 17; 26; …}.

Mà x là chữ số nên x = 8.

Vậy x = 8.

Câu 3:

Gọi số người tham gia buổi tập đồng diễn thể dục là x (x ∈ N, 400 < x < 500).

Do số người tham gia xếp thàng hàng 5, hàng 6 và hàng 8 đều thừa một người nên ta có:

x – 1 5

x – 16

x – 18

nên x – 1 ∈ BC(5, 6, 8).

Ta có 5 = 5, 6 = 2.3, 8 = 2³.

Khi đó: BCNN(5, 6, 8) = 2³.3.5 = 8.3.5 = 120.

Suy ra BC(5, 6, 8) = B(120) = {0; 120; 240; 360; 480; 600; …}.

Do đó x – 1 ∈ {0; 120; 240; 360; 480; 600; …}.

Hay x ∈ {1; 121; 241; 361; 481; 601; …}.

Mà 400 < x < 500 nên x = 481. 

Câu 4:

Gọi số chia và thương lần lượt là b và q (b; q ∈ N, b ≠0).

Như vậy 89 : b = q (dư 12) và b > 12 (số chia lớn hơn số dư).

Từ đó 89 = bq + 12. Suy ra bq = 89 – 12 = 77 = 7 . 11 = 77 . 1

Mà b > 12 nên b = 77 và q = 1.

Do đó 89 : 77 = 1 (dư 12).

Vậy số chia bằng 77, thương bằng 1.

Câu 5:

Ta có: A = n² + n + 1 = n(n+1)+1

Vì n ∈ N nên n + 1 ∈ N. 

Nếu n là số chẵn thì n(n + 1) chia hết cho 2.

Nếu n là số lẻ thì n + 1 là số chẵn nên n(n + 1) chia hết cho 2.

Do đó n(n + 1) chia hết cho 2 với mọi số tự nhiên n.

Mà 1 không chia hết cho 2 nên n(n+1) + 1 không chia hết cho 2.

Suy ra n(n + 1) + 1 không chia hết cho 2 với mọi số tự nhiên n.

Vậy A không chia hết cho 4 với mọi số tự nhiên n.

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2023 có đáp án - Đề số 7

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 6

Thời gian làm bài: .........

A. Phần đề bài

I. Trắc nghiệm (2 điểm)

Câu 1. Cho tập hợp A = {chó, mèo, lợn, gà}. Phát biểu nào dưới đây là đúng?

A. Chó ∈ A;

B. Mèo ∉ A;

C. Cá ∈ A;

D. Lợn ∉ A.

Câu 2. Chữ số 2 trong số 123 857 có giá trị là:

A. 120 000

B. 20 000

C. 23 857

D. 20

Câu 3. Trong các số sau: 114, 76; 1 029; 354; 57. Có bao nhiêu số chia hết cho 3?

A. 3

B. 0

C. 5

D. 4

Câu 4. Kết quả của phép tính sau: 7⁸ : 7

A. 7⁸;

B. 7⁶;

C. 7⁷;

D. 7⁹.

II. Tự luận (8 điểm)

Bài 1. (2 điểm) Thực hiện phép tính:

a) 12 + 3.2⁵ : 4 – 3;

b) 120 + [55 – (11 – 3.2)²] + 2³;

c) 24⁰.14.83 + 7.2.17.

Bài 2. (2 điểm) Tìm x, biết:

a) 2x + 15 = 242:2;

b) (3x – 4)³ = 125;

c) x ∈ ƯC(18,54) và x > 6.

Bài 3. (1 điểm) Cho tập hợp A là tập hợp các số tự nhiên chia hết cho 2 và 5, lớn hơn 12 nhỏ hơn hoặc bằng 70. Hãy viết tập hợp A theo hai cách.

Bài 4. (1,5 điểm) Tuấn và Hà mỗi người mua một số hộp bút chì màu, trong mỗi hộp đều có từ hai chiếc bút trở lên và số bút trong mỗi hộp là như nhau. Tính ra Tuấn mua 25 bút, Hà mua 20 bút. Hỏi mỗi hộp bút chì màu có bao nhiêu chiếc?

Bài 5. (0,5 điểm) Tìm số tự nhiên có hai chữ số biết số đó chia cho tổng các chữ số của nó thu được 7 dư 6.

B. Đáp án và hướng dẫn giải

I. Phần trắc nghiệm

Bảng đáp án (0,5 × 4 = 2 điểm)

Câu 1: A

Câu 2: B

Câu 3: D

Câu 4: C

 

Hướng dẫn chi tiết

Câu 1:

Ta có:

Chó là một phần tử của tập hợp A nên ta viết chó ∈ A. Do đó A đúng.

Mèo là một phần tử của tập hợp A nên ta viết mèo ∈ A. Do đó B sai.

Cá không phải là phần tử của tập hợp A nên ta viết cá ∉ A. Do đó C sai.

Lợn là một phần tử của tập hợp A nên ta viết lợn ∈ A. Do đó D sai.

Chọn A.

Câu 2:

Trong số 123 857, chữ số 2 là chữ số hàng chục nghìn nên chữ số 2 có giá trị 2.10 000 = 20 000.

Chọn B.

Câu 3:

Ta có:

1 + 1 + 4 = 6 chia hết cho 3 nên 114 chia hết cho 3;

7 + 6 = 13 không chia hết cho 3 nên 76 không chia hết cho 3;

1 + 0 + 2 + 9 = 12 chia hết cho 3 nên 1 029 chia hết cho 3;

3 + 5 + 4 = 12 chia hết cho 3 nên 354 chia hết cho 3;

5 + 7 = 12 chia hết cho 3 nên 57 chia hết cho 3.

Vậy có 4 số chia hết cho 3.

Chọn D

Câu 4:

Ta có: 7⁸ : 7 = 7^{8 – 1} = 7⁷.

Chọn C.

II. Tự luận

Bài 1:

a) 12 + 3.2⁵ : 4 – 3

= 12 + 3.32:4 – 3

= 12 + 3.8 – 4

= 12 + 24 – 4

= 36 – 4

= 32

b) 120 + [55 – (11 – 3.2)²] + 2³

= 120 + [55 – (11 – 6)²] + 8

= 120 + [55 – 4²] + 8

= 120 + [55 – 16] + 8

= 120 + 39 + 8

= 159 + 8

= 167

c) 24⁰.14.83 + 7.2.17

= 14.83 + 14.17

= 14.(83 + 17)

= 14.100

= 1 400.

Bài 2:

a) 2x + 15 = 242:2

2x + 15 = 121

2x = 121 – 15

2x = 106

x = 106 : 2

x = 53.

Vậy x = 53.

b) (3x – 4)³ = 125

(3x – 4)³ = 5³

3x – 4 = 5

3x = 5 + 4

3x = 9

x = 9:3

x = 3.

Vậy x = 3.

c) x ƯC(18,54) và x > 6

Ta có: 18 = 2.3², 54 = 2.3³

Khi đó: ƯCLN(18, 54) = 2.3² = 18.

ƯC(18,54) = Ư(18) = {1; 2; 3; 6; 9; 18}

x ∈ {1; 2; 3; 6; 9; 18}

Mà x > 6 nên x ∈ {9; 18}.

Vậy x ∈ {9; 18}.

Bài 3:

Các số tự nhiên chia hết cho 2 và cho 5 là các số tự nhiên có chữ số tận cùng bằng 0: 0; 10; 20; 30; 40; 50; 60; 70; 80; …

Các số tự nhiên ở trên thỏa mãn lớn hơn 12 nhỏ hơn hoặc bằng 70 là: 20; 30; 40; 50; 60; 70.

Theo cách liệt kê, tập hợp A được mô tả: A = {20; 30; 40; 50; 60; 70}.

Theo cách chỉ ra tính chất đặc trưng, ta viết: {x ∈ N|x2, x5, 12 < x ≤ 70}

Bài 4:

Gọi số bút trong mỗi hộp bút chì màu là x ( x ∈ N, x > 2) (chiếc).

Vì số bút trong mỗi hộp là như nhau nên 25 và 20 chia hết cho x hay x ƯC(25, 20).

Ta có: 25 = 5², 20 = 2².5;

ƯCLN(25, 20) = 5.

ƯC(25, 20) = Ư(5) = {1; 5}

x ∈ {1; 5}

Mà x > 2 nên x = 5 (thỏa mãn điều kiện).

Vậy trong mỗi hộp có 5 chiếc bút.

Bài 5:

Gọi số tự nhiên có hai chữ số cần tìm là  (Với a,b {0;1;2;3; …; 9} và a ≠ 0 )

Ta có tổng các chữ số của nó là: a + b.

Vì số dư phép chia là 6 nên a + b > 6.

Theo đầu bài ta có:    = 7(a + b) + 6

10a + b = 7a + 7b + 6

3a = 6b + 6

a = 2b + 2

a = 2(b + 1)

Mà 0 < a ≤ 9 ⇔ 0 < 2(b + 1) ≤ 9 ⇒ 0 < b + 1 < 4,5.

Do đó 0 ≤ b < 5.

Ta có bảng sau:

b	a = 2(b + 1)	a + b (a + b > 6)
0	2	3 (loại)
1	4	5 (loại)
2	6	8 (thỏa mãn)
3	8	11 (thỏa mãn)
4	10 (loại)

 Vậy số cần tìm là 62 và 83.

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2023 có đáp án - Đề số 8

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 6

Thời gian làm bài: .........

I. Phần trắc nghiệm

Câu 1: Trong các hình sau đây hình nào là hình vuông?

Hình a	Hình b
Hình c	Hình d

A) Hình a

B) Hình b

C) Hình c

D) Hình d

Câu 2: Phân tích số 108 ra thừa số nguyên tố ta được:

A)  2².3³

B) 3².2²  

C)  3².2³

D) 3³.2³

Câu 3: Từ 35 đến 60 có bao nhiêu số nguyên tố:

A) 4 số

B) 7 số 

C) 5 số

D) 6 số

Câu 4: Kết quả của phép tính 2³.3 - (1¹⁰ +15) : 16 là:

A) 22

B) 23

C) 24

D) 25

Câu 5: Chọn câu sai trong các câu dưới đây

A) Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA

B) Sáu góc đỉnh A, B, C, D, E, G bằng nhau.

C) Ba đường chéo chính là AD, BE, CG bằng nhau

D) Các đoạn thẳng BG = CG.

Câu 6: Tìm số tự nhiên x thỏa mãn:3² + 2x + 6 = 21

A) 2

B) 5

C) 3

D) 4

Câu 7: Diện tích tam giác có chiều cao là 5cm và độ dài cạnh đáy tương ứng là 8cm là:

A) 20 cm² 

B) 15 cm² 

C) 40 cm² 

D) 25 cm²

Câu 8: Chọn câu sai trong các câu dưới đây:

Cho hình thoi ABCD 

A) AB song song với CD và BC song song với AD.

B) AB = BC = CD= AD

C) AC và BD vuông góc với nhau

D) Bốn góc đỉnh A, B, C, D bằng nhau.

II. Phần tự luận

Bài 1: Thực hiện phép tính

a) 2¹¹ :  

b)  6².10 : {780 : [10³ - (2.5³ + 35.14)]}

Bài 2: Tìm x

a) 2x + 15 = 142:2

b) (x + 1) + (x + 2) + (x + 3) + … + (x + 10) = 75

Bài 3: Tính chu vi và diện tích hình chữ nhật có chiều dài là 12cm và chiều rộng là 8cm.

Bài 4: Lớp bạn Hoa cần chia 171 chiếc bút bi, 63 chiếc bút chì và 27 cục tẩy vào trong các túi quà mang đi tặng ở trung tâm trẻ mồ côi sao cho số bút bi, bút chì và cục tẩy ở mỗi bên đều như nhau. Tính số lượng túi quà nhiều nhất mà các bạn lớp Hoa có thể chia. Khi đó, số lượng của mỗi loại bút bi, bút chì, cục tẩy trong mỗi túi quà là bao nhiêu.

Bài 5: Cho A = 1 + 3 + 3² + 3³ + ... + 3¹⁰¹ . Chứng minh rằng A chia hết cho 13.

Đáp án

I. Phần tắc nghiệm

Câu 1: Trong các hình sau đây hình nào là hình vuông?

Hình a	Hình b
Hình c	Hình d

A) Hình a

B) Hình b

C) Hình c

D) Hình d

Giải thích vì hình b có 4 góc vuông và 4 cạnh bằng nhau nên nó là hình vuông.

Câu 2: Phân tích số 108 ra thừa số nguyên tố ta được:

A) 2².3³ 

B)  2².3²

C)  3².2³

D) 3³.2³ 

Do đó 108 = 2².3³

Câu 3: Từ 35 đến 60 có bao nhiêu số nguyên tố:

A) 4 số

B) 7 số 

C) 5 số

D) 6 số

Từ 35 đến 60 có các số nguyên tố là: 37; 41; 43; 47; 53; 59. Vậy có 6 số nguyên  tố nằm giữa 35 đến 60

Câu 4: Kết quả của phép tính 2³. 3 - (1¹⁰ + 15) : 16 là:

A) 22

B) 23

C) 24

D) 25

 2³. 3 - (1¹⁰ + 15) : 16

= 8.3 – (1 + 15):16

= 24 – 16:16

= 24 – 1 = 23

Câu 5: Chọn câu sai trong các câu dưới đây

A) Sáu cạnh bằng nhau: AB = BC = CD = DE = EG = GA

B) Sáu góc đỉnh A, B, C, D, E, G bằng nhau.

C) Ba đường chéo chính là AD, BE, CG bằng nhau

D) Các đoạn thẳng BG = CG.

Vì BG không phải đường chéo chính nên không bằng CG.

Câu 6: Tìm số tự nhiên x thỏa mãn: 3² + 2x + 6 = 21 

A) 2

B) 5

C) 3

D) 4

3² + 2x + 6 = 21

9 + 2x + 6 = 21

9 + 2x = 21 – 6

9 + 2x = 15

2x = 15 – 9

2x = 6

x = 6:2

x = 3

Câu 7: Diện tích tam giác có chiều cao là 5cm và độ dài cạnh đáy tương ứng là 8cm là:

A) 20 cm²

B) 15 cm²

C) 40 cm²

D) 25 cm²

Diện tích tam giác là:

S = a.h:2 = 8.5:2 = 20 cm²

Câu 8: Chọn câu sai trong các câu dưới đây:

Cho hình thoi ABCD 

A) AB song song với CD và BC song song với AD.

B) AB = BC = CD= AD

C) AC và BD vuông góc với nhau

D) Bốn góc đỉnh A, B, C, D bằng nhau.

Ta thấy chỉ có hai đỉnh đối diện góc mới bằng nhau.

II. Phần tự luận

Bài 1: 

a)  2¹¹ : {1026 - [(3⁴ + 1) : 41]}

=  2¹¹ : {1026 - [(81 + 1) : 41]}

= 2¹¹ : {1026 - [82 : 41]}

= 2¹¹ :  {1026 - 2}

= 2¹¹ : 1024

= 2048:1024

= 2

b)  6².10:{780 : [10³ - (2.5³ + 35.14)]}

= 36.10:{780 : [10³ - (2.125 + 35.14)]}

= 36.10:{780 : [1000 - (250 + 490)]}

=  36.10:{780 : [1000 - 740]}

=  36.10:{780: 260}

=  36.10:3

= 360:3

=120

Bài 2: Tìm x

a) 2x + 15 = 142:2

2x + 15 = 71

2x = 71 – 15

2x = 56

x = 56:2

x = 28

Vậy x = 28

b) (x + 1) + (x + 2) + (x + 3) + … + (x + 10) = 75

x + 1 + x + 2 + x + 3 + … + x + 10 = 75

(x + x + …+ x) + (1 + 2 + 3 +… + 10) = 75

10x + (1 + 2 + 3 + … + 10) = 75

Ta tính B = 1 + 2 + …+ 10 = (1 + 10) + (2 + 9)+ (3 + 8) + (4 + 7) + (5 + 6) 

B = 11 + 11 + 11 + 11 + 11 = 55.

Ta có: 10x + 55 = 75

10x = 75 – 55

10x = 20 

x = 20:10

x = 2

Vậy x = 2.

Bài 3:

Lời giải:

Chu vi hình chữ nhật là:

P = (a + b).2 = (12 + 8).2 = 40cm

Diện tích hình chữ nhật là

S = a.b = 12.8 = 96 cm² 

Vậy chu vi hình chữ nhật là 40cm, diện tích hình chữ nhật là 96cm² .

Bài 4: 

Lời giải:

Gọi số túi quà lớp bạn Hoa mang tặng là x (x ∈ N^*)

Vì chia đều 171 chiếc bút bi, 63 chiếc bút chì và 27 cục tẩy vào các túi quà nên 171 x; 63 x; 27 x hay x là ước chung của 171; 63; 27.

Vì số túi quà chia được là lớn nhất nên x là ước chung lớn nhất của 171; 63; 27.

Ta có:

171 = 3.3.19 = 3² .19

63 = 3.3.7 = 3² . 19 

27 = 3.3.3 = 3³ 

ƯCLN (171; 63; 27) = 3²  = 9 

Vậy số túi quà nhiều nhất là 9 túi

Số bút bi trong mỗi túi quà là:

171:9 = 19 (chiếc bút bi)

Số bút chì trong mỗi túi quà là:

63:9 = 7 (chiếc bút chì)

Số cục tẩy trong mỗi túi quà là:

27:9 = 3 (cục tẩy)

Bài 5: Cho A = 1 + 3 + 3² + 3³ + ... + 3¹⁰¹ . Chứng minh rằng A chia hết cho 13.

Lời giải:

A = 1 + 3 + 3² + 3³ + 3⁴ + 3⁵) + ... + 3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹

A = (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)

A =  (1 + 3 + 3²) + 3³ (1 + 3 + 3²)+ ... + 3⁹⁹( 1 + 3 + 3²) 

A = (1 + 3 + 3²)(1 + 3³ + 3⁶ + ... + 3⁹⁹)

A = 13. (1 + 3³ + 3⁶ + ... + 3⁹⁹)

Vì 13 chia hết cho 13 nên 13.(1 + 3³ + 3⁶ + ... + 3⁹⁹) chia hết cho 13 nên A chia hết cho 13 

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2024 có đáp án - Đề số 9

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 6

Thời gian làm bài: .........

I. Phần trắc nghiệm (4 điểm)

Câu 1: Cho tập hợp . Chọn khẳng định đúng.

A.

B.

C.

D.

Câu 2: Tập hợp  có số phần tử là:

A. 99

B. 100

C. 101

D. 102

Câu 3: Số vừa chia hết cho 3 vừa chia hết cho 5 là:

A. 425

B. 693

C. 660

D. 256

Câu 4: Lũy thừa với số mũ tự nhiên có tính chất nào sau đây?

A.	B.
C.	D.

Câu 5: Cặp số chia hết cho 2 là:

A. (234; 415)	B. (312; 450)
C. (675; 530)	D. (987; 123)

Câu 6: Tìm khẳng định đúng trong các khẳng định sau:

A. Một số chia hết cho 9 thì luôn chia hết cho 3

B. Nếu hai số chia hết cho 3 thì tổng của hai số đó chia hết cho 9

C. Mọi số chẵn thì luôn chia hết cho 5

D. Số chia hết cho 2 là số có chữ số tận cùng bằng 0; 2; 3; 4; 6; 8

Câu 7: Số 41 là

A. hợp số

B. không phải số nguyên tố

C. Số nguyên tố

D. không phải hợp số

Câu 8: Các cặp số nào sau đây nguyên tố cùng nhau?

A. 3 và 11	B. 4 và 6
C. 2 và 6	D. 9 và 12

II. Phần tự luận (6 điểm)

Câu 1: Thực hiện các phép tính:

a. 

b. 

c. 

d. 

Câu 2: Tìm x biết:

a. 

b. 

c. 

d.  và x lớn nhất

Câu 3: Một đội y tế có 280 nam, 220 nữ dự định chia thành các nhóm sao cho số nam và số nữ ở mỗi nhóm đều nhau, biết số nhóm chia được nhiều hơn 1 nhóm và không lớn hơn 5 nhóm. Hỏi có thể chia đội thành mấy nhóm? Khi đó mỗi nhóm có bao nhiêu nam, bao nhiêu nữ?

Câu 4: Cho . Chứng minh rằng A chia hết cho 13

Đáp án Đề thi Toán lớp 6 giữa học kì 1

I. Phần trắc nghiệm (4 điểm)

II. Phần tự luận (6 điểm)

Câu 1:

a. 

b. 

c. 

d. 

Câu 2:

a. 

Vậy x = 28

b. 

Vậy x = 5

c. 

Vậy x = 11

d. Ta có: 

Ta lại có:

Do x lớn nhất => x = 5

Câu 3:

Gọi số nhóm cần chia là x (x > 1)

Ta có: Đội y tế có 280 nam, 220 nữ dự định chia thành các nhóm sao cho số nam và số nữ ở mỗi nhóm đều nhau.

280 ⋮ x ; 220 ⋮ x. Vậy x ∈ UC (280, 220)

Ta có:

280 = 2³.5. 7

220 = 2².5.11

Suy ra: UCLN (280, 220) = 2².5

UC (280, 220) = U(20) {1; 2; 4; 5; 10; 20}

Do số nhóm chia được nhiều hơn 1 nhóm và không lớn hơn 5 nhóm

x∈ {2; 4; 5}

Ta có bảng sau:

Số nhóm	Số người nữ trong nhóm	Số nam trong nhóm
2	110	140
4	55	70
5	44	56

Câu 4

Đề thi Giữa Học kì 1 Toán lớp 6 Kết nối tri thức năm 2024 có đáp án - Đề số 10

Phòng Giáo dục và Đào tạo .....

Đề khảo sát chất lượng Giữa Học kì 1

Năm học ...

Môn: Toán 6

Thời gian làm bài: .........

I. TRẮC NGHIỆM: (3,0 điểm)

Khoanh tròn vào chữ cái đứng trước câu trả lời đúng trong mỗi câu sau:

Câu 1. Cho tập hợp A = {a; b; c; d}, khẳng định nào sau đây là đúng?

A. c ∈ A
B. d ∈ A
C. e ∈ A
D. a ∉ A

Câu 2. Tập hợp nào sau đây chỉ gồm các phần tử là số tự nhiên?

A. 
B. {1; 2; 3}
C. 
D. {0; 2; 4}

Câu 3. Với a, m, n là các số tự nhiên, khẳng định nào sau đây đúng?

A. a^m . aⁿ = a^m + n (a ≠ 0)
B. a^m . aⁿ = a^m.n (a ≠ 0)
C. a^m : aⁿ = a^m.n (a ≠ 0)
D. a^m : aⁿ = m – n (a ≠ 0)

Câu 4. Thứ tự thực hiện các phép tính trong biểu thức không chứa dấu ngoặc là:

A. Lũy thừa → Nhân, chia → Cộng, trừ.
B. Nhân chia → Cộng trừ → Lũy thừa.
C. Nhân chia → Lũy thừa → Cộng, trừ.
D. Cộng, trừ → Nhân, chia → Lũy thừa.

Câu 5. Kết quả của phép tính 2³. 2² là:

A. 4⁵
B. 2⁵
C. 2⁶
D. 4⁶

Câu 6. Số tự nhiên nào sau đây chia cho 5 dư 2?

A. 4
B. 5
C. 6
D. 7

Câu 7. Số tự nhiên nào sau đây chia hết cho cả 2 và 5?

A. 126
B. 259
C. 430
D. 305

Câu 8. Trong các số tự nhiên sau, số nào là số nguyên tố?

A. 4
B. 7
C. 18
D. 25

Câu 9. Số tự nhiên nào sau đây là ước của 10?

A. 0
B. 3
C. 2
D. 11

Câu 10. Số tự nhiên nào sau đây là BCNN(4, 6)?

A. 15
B. 12
C. 10
D. 9

Câu 11. Khi mô tả các yếu tố của hình vuông, khẳng định nào sau đây sai:

A. Hình vuông có 4 cạnh bằng nhau;
B. Hình vuông có 4 góc vuông;
C. Hình vuông có các cạnh đối không bằng nhau;
D. Hình vuông có hai đường chéo bằng nhau.

Câu 12. Hình nào sau đây là hình chữ nhật?

II. TỰ LUẬN: (7,0 điểm)

Câu 1. (1,0 điểm) Trong hình vẽ bên có bao nhiêu tam giác đều? Hãy viết tên các tam giác đều đó.

Câu 2. (2,0 điểm)

a) Viết tập hợp A các số tự nhiên không vượt quá 7.

b) Viết các số 23 và 29 bằng số La Mã.

Câu 3. (1,5 điểm)

a) Thực hiện phép tính: ( tính hợp lý nếu có thể) 12. 35 + 12. 65

b) Tìm x, biết: (123 - 4x) - 67 = 2³

Câu 4. (1,5 điểm)

a) Tìm tập hợp BC (30; 45)

b) Một đội y tế có 24 bác sĩ và 108 y tá. Có thế chia đội y tế đó nhiều nhất thành mấy tổ để số y tá được chia đều vào các tổ ?

Câu 5. (1,0 điểm) Tìm n ∈ N biết để 3 chia hết cho n + 2.

Đáp án đề thi giữa kì 1 môn Toán 6 năm 2022 - 2023

I. TRẮC NGHIỆM (3,0 điểm) Mỗi câu trả lời đúng: 0,25 điểm

II. TỰ LUẬN ( 7,0 điểm)