Trắc nghiệm Toán 10 CTST Bài 2: Hệ bất phương trình bậc nhất hai ẩn có đáp án
Dạng 3: Ứng dụng hệ bất phương trình bậc nhất hai ẩn để giải bài toán kinh tế có đáp án
-
338 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
15/07/2024Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lợi nhuận 40 000 đồng. Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lợi nhuận 30 000 đồng. Xưởng có 200 kg nguyên liệu và 1 200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lợi nhuận cao nhất ?
Xem đáp án
Đáp án đúng là: A
Gọi x (x ≥ 0 (1)) là số kg loại I cần sản xuất, y (y ≥ 0 (2)) là số kg loại II cần sản xuất.
Số nguyên liệu cần dùng để sản xuất x sản phẩm loại I là: 2x
Số nguyên liệu cần dùng để sản xuất y sản phẩm loại II là: 4y
Xưởng có 200 kg nguyên liệu nên ta có: 2x + 4y ≤ 200 ⇔ x + 2y ≤ 100 ⇔ x + 2y – 100 ≤ 0 (3)
Thời gian để sản xuất x sản phẩm loại I là: 30x
Thời gian để sản xuất y sản phẩm loại II là: 15y
Xưởng có 1 200 giờ làm việc nên ta có: 30x + 15y ≤ 1200 hay 2x + y – 80 ≤ 0 (4)
Xét bất phương trình (1) và điểm A(1; 2) có:
Điểm A không nằm trên đường thẳng x = 0 và 1 ≥ 0, do đó, miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng có kể bờ x = 0 và chứa điểm A(1; 2).
Xét bất phương trình (2) và điểm B(0; 1) có:
Điểm B không nằm trên đường thẳng y = 0 và 1 ≥ 0, do đó, miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng có kể bờ y = 0 và chứa điểm B(0; 1)
Xét bất phương trình (3) và điểm (0; 0) ta có:
Điểm (0; 0) không nằm trên đường thẳng x + 2y – 100 = 0 và 0 + 2.0 – 100 = –100 < 0 nên miền nghiệm của bất phương trình (3) là nửa mặt phẳng có kể bờ x + 2y – 100 = 0 và chứa điểm (0; 0).
Xét bất phương trình (4) và điểm (0; 0) ta có:
Điểm (0; 0) không nằm trên đường thẳng 2x + y – 80 = 0 và 2.0 + 0 – 80 = –80 < 0 nên miền nghiệm của bất phương trình (4) là nửa mặt phẳng có kể bờ 2x + y – 80 = 0 và chứa điểm (0; 0)
Kết hợp miền nghiệm của các bất phương trình (1), (2), (3) và (4) là miền nghiệm thỏa mãn màu trắng trong hình vẽ:
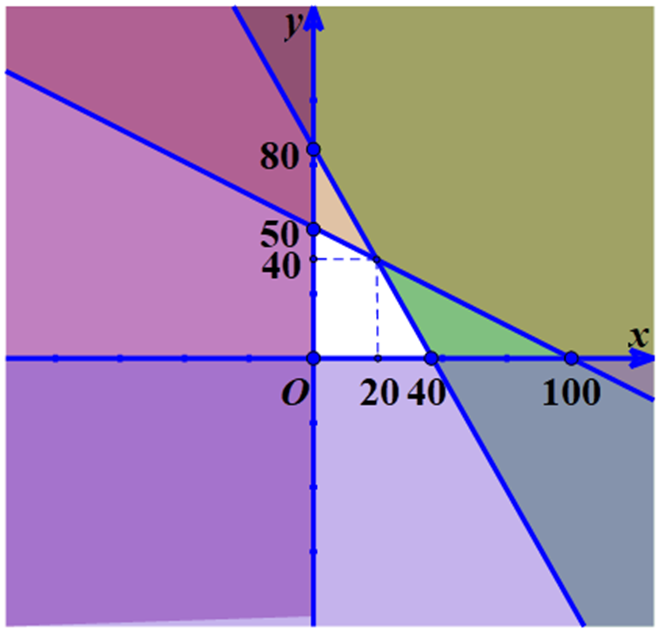
Lợi nhuận thu lại từ x sản phẩm loại I là: 40 000x
Lợi nhuận thu lại từ y sản phẩm loại II là: 30 000y
Tổng lợi nhuận là: 40 000x + 30 000y
Giá trị lớn nhất của L(x; y) = 40 000x + 30 000y đạt tại một trong các điểm (0; 0), (40; 0), (0; 50), (20; 40).
Ta có:
L(0; 0) = 0
L(40; 0) = 1 600 000
L(0; 50) = 1 500 000
L(20; 40) = 2 000 000
Vậy giá trị lớn nhất của L(x; y) là 2 000 000 khi (x; y) = (20; 40).
Vậy cần sản xuất 20kg sản phẩm loại I và 40kg sản phẩm loại II để có mức lợi nhuận lớn nhất
Câu 2:
19/07/2024Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1g hương liệu; pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để được số điểm thưởng là lớn nhất.
Xem đáp án
Đáp án đúng là: B
Gọi x, y lần lượt là số lít nước cam và táo của một đội pha chế (x, y ≥ 0).
Số điểm thưởng của đội chơi này là: Đ(x; y) = 60x + 80y
Số gam đường cần dùng là 30x + 10y.
Số lít nước cần dùng là x + y.
Số gam hương liệu cần dùng là x + 4y.
Vì trong cuộc thi pha chế, mỗi đội chơi sử dụng tối đa 24g hương liệu, 9 lít nước và 210 g đường nên ta có hệ bất phương trình
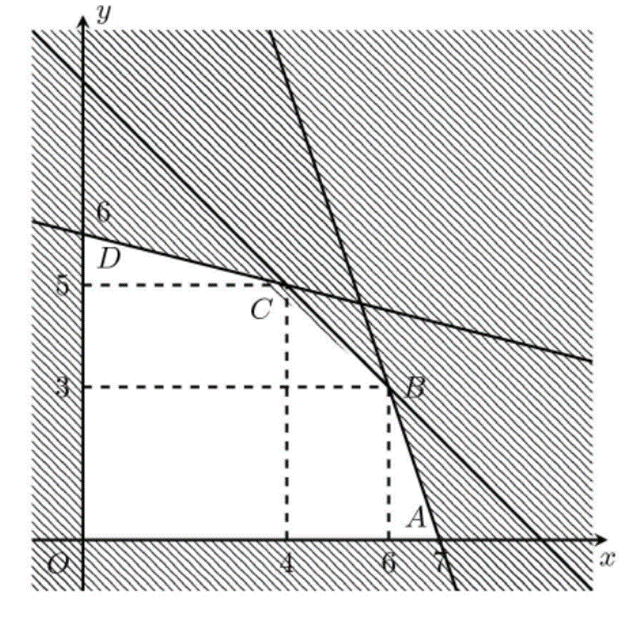
Miền nghiệm của hệ trên là ngũ giác OABCD (kể cả biên). Ta có: Đ(x; y) = 60x + 80y sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ đã cho khi (x; y) là tọa độ của một trong các đỉnh O(0; 0), A(7; 0), B(6; 3), C(4; 5), D(0; 6).
Ta có:
Đ(0; 0) = 60.0 + 80.0 = 0
Đ(7; 0) = 60.7 + 80.0 = 420
Đ(6; 3) = 60.6 + 80.3 = 600
Đ(4; 5) = 60.4 + 80.5 = 640
Đ(0; 6) = 60.0 + 80.6 = 480
Vậy giá trị lớn nhất của D(x; y) là 640 hay để được số điểm thưởng lớn nhất thì cần pha chế 4 lít nước cam và 5 lít nước táo.
Câu 3:
13/07/2024Trong cuộc thi gói bánh vào dịp năm mới, mỗi đội chơi được sử dụng tối đa 20 kg gạo nếp, 2 kg thịt, 5 kg đậu xanh để gói bánh chưng và bánh ống. Để gói một cái bánh chưng cần 0,4 kg gạo nếp, 0,05 kg thịt và 0,1 kg đậu xanh. Để gói một cái bánh ống cần 0,6 kg gạo nếp, 0,075 kg thịt và 0,15 kg đậu xanh. Mỗi cái bánh chưng nhận được 5 điểm thưởng, mỗi cái bánh ống nhận được 7 điểm thưởng. Hỏi cần phải gói mấy cái bánh mỗi loại để được nhiều điểm thưởng nhất ?
Xem đáp án
Đáp án đúng là: A
Gọi số bánh chưng gói được là x, số bánh ống gói được là y. (x, y ≥ 0)
Khi đó số điểm thưởng là F(x; y) = 5x + 7y
Số kg gạo nếp cần dùng là 0,4x + 0,6y
Số kg thịt cần dùng là 0,05x + 0,075y
Số kg đậu xanh cần dùng là 0,1x + 0,15y
Vì trong cuộc thi này chỉ được sử dụng tối đa 20kg gạo nếp, 2kg thịt ba chỉ và 5kg đậu xanh nên ta có hệ bất phương trình
Miền nghiệm của hệ bất phương trình là tam giác OAB (kể cả biên)
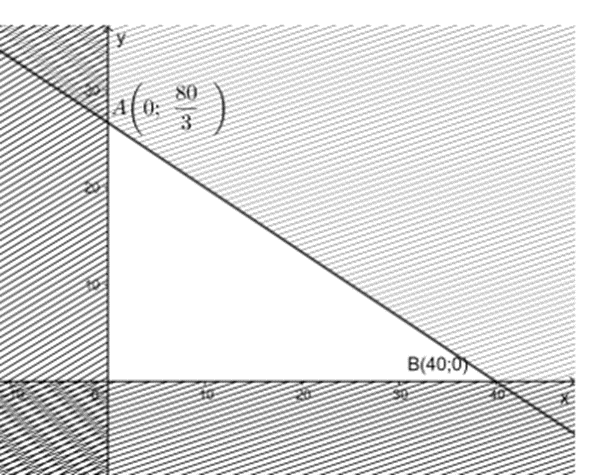
F(x; y) sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình trên khi (x; y) là tọa độ một trong các đỉnh O(0; 0), A, B(40; 0) (loại điểm A vì số bánh phải là số nguyên).
Ta có:
F(0; 0) = 5.0 + 7.0 = 0
F(40; 0) = 5.40 + 7.0 = 200
Do đó, F(x; y) lớn nhất là 200. Vậy cần phải gói 40 cái bánh chưng để nhận được số điểm thưởng là lớn nhất.
Câu 4:
23/07/2024Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kg thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua tối đa 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tiền 1 kg thịt bò là 45 nghìn đồng, 1 kg thịt lợn là 35 nghìn đồng. Hỏi gia đình đó phải mua bao nhiêu kg thịt mỗi loại để số tiền bỏ ra là ít nhất ?
Xem đáp án
Đáp án đúng là: D
Gọi x và y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó mua mỗi ngày (0 ≤ x ≤ 1,6; 0 ≤ y ≤ 1,1)
Khi đó, chi phí để mua số thịt là: F(x; y) = 45x + 35y.
Trong x kg thịt bò có 800x đơn vị protein và 200x đơn vị lipit.
Trong y kg thịt lợn có 600y đơn vị protein và 400y đơn vị lipit.
Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày nên ta có hệ bất phương trình:
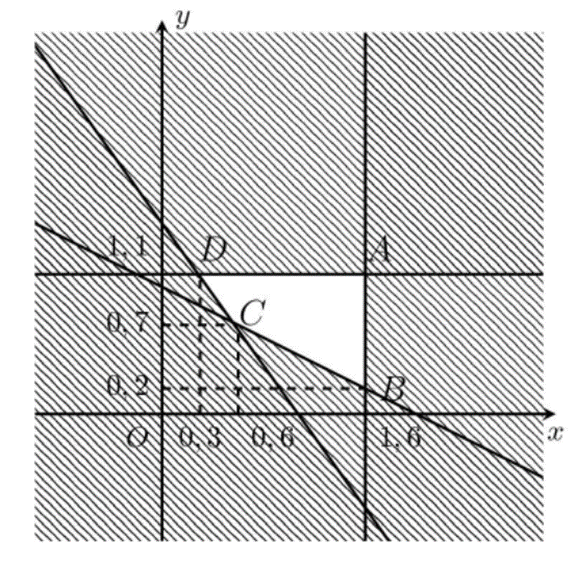
Miền nghiệm của hệ bất phương trình trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên).
Ta có:
F(1,6; 1,1) = 45.1,6 + 35.1,1 = 110,5
F(1,6; 0,2) = 45.1,6 + 35.0,2 = 79
F(0,6; 0,7) = 45.0,6 + 35.0,7 = 51,5
F(0,3; 1,1) = 45.0,3 + 35.1,1 = 52
Vậy F(x; y) nhỏ nhất là 51,5 hay gia đình này cần phải mua 0,6 kg thịt bò và 0,7 kg thịt lợn để số tiền bỏ ra là ít nhất.
Câu 5:
21/07/2024Một gia đình định trồng cà phê và ca cao trên diện tích 10 ha. Nếu trồng cà phê thì cần 20 công và thu về 10 000 000 đồng trên diện tích mỗi ha, nếu trồng ca cao thì cần 30 công và thu 12 000 000 đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được nhiều tiền nhất. Biết rằng cà phê do các thành viên trong gia đình tự chăm sóc và số công không vượt quá 80, còn ca cao gia đình thuê người làm với giá 100 000 đồng cho mỗi công ?
Xem đáp án
Đáp án đúng là: B
Gọi x và y lần lượt là số ha cà phê và ca cao mà hộ nông dân này trồng (x ≥ 0, y ≥ 0).
Số tiền cần bỏ ra để thuê người trồng ca cao là 30y.100 000 = 3 000 000y (đồng).
Lợi nhuận thu được là: F(x; y) = 10 000 000x + 12 000 000 – 3 000 000y = 10 000 000x + 9 000 000 y.
Vì số công để trồng cà phê không vượt quá 80 công và gia đình chỉ có 10 ha đất nên ta có hệ phương trình:
Miền nghiệm của hệ trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên). F(x; y) đạt giá trị lớn nhất khi (x; y) là tọa độ của một trong các đỉnh tứ giác.
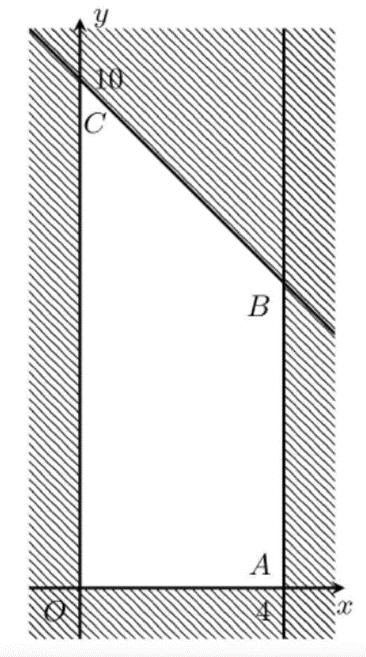
Ta có:
F(0; 0) = 0
F(4; 0) = 40 000 000
F(4; 6) = 94 000 000
F(0; 10) = 90 000 000
Vậy F(x; y) lớn nhất khi (x; y) = (4; 6) hay cần phải trồng 4 ha cà phê và 6 ha ca cao để thu về lợi nhuận lớn nhất.
Câu 6:
21/07/2024Một nông dân định trồng đậu và cà trên diện tích 8 ha. Nếu trồng đậu thì cần 20 công và thu 3 000 000 đồng trên diện tích mỗi ha, nếu trồng cà thì cần 30 công và thu 4 000 000 đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được nhiều tiền nhất biết rằng tổng số công không quá 180 ?
Xem đáp án
Đáp án đúng là: A
Số ha đậu và cà mà hộ nông dân này trồng lần lượt là x và y (x, y ≥ 0).
Lợi nhuận thu được là F(x; y) = 3 000 000x + 4 000 000y (đồng).
Tổng số công dùng để trồng x ha đậu và y ha cà là 20x + 30y.
Ta có hệ bất phương trình:
Miền nghiệm của hệ bất phương trình trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên).
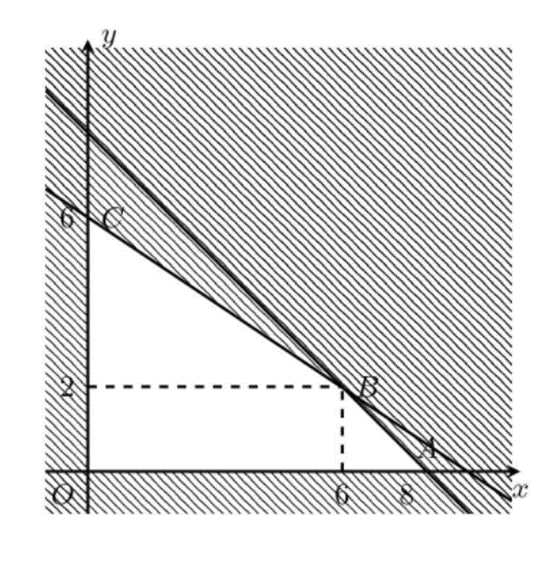
F(x; y) đạt giá trị lớn nhất khi (x; y) là tọa độ của một trong các đỉnh của tứ giác.
Ta có:
F(0; 0) = 0
F(8; 0) = 24 000 000
F(6; 2) = 26 000 000
F(0; 6) = 24 000 000
Suy ra F(x; y) lớn nhất khi (x; y) = (6; 2) tức là hộ nông dân này cần phải trồng 6 ha đậu và 2 ha cà thì sẽ thu về lợi nhuận lớn nhất.
Câu 7:
19/07/2024Một phân xưởng có hai máy đặc chủng loại 1 và loại 2 sản xuất hai loại sản phẩm kí hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy loại 1 trong 3 giờ và máy loại 2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy loại 1 trong 1 giờ và máy loại 2 trong 1 giờ. Máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày. Hỏi cần sản xuất bao nhiêu tấn sản phẩm loại A và loại B để số tiền lãi mà phân xưởng này có thể thu được trong một ngày là lớn nhất?
Xem đáp án
Đáp án đúng là: A
Gọi x, y lần lượt là số tấn sản phẩm loại A, B mà phân xưởng sản xuất trong 1 ngày (x ≥ 0, y ≥ 0).
Khi đó, số tiền lãi một ngày là: F(x; y) = 2x + 1,6y (triệu đồng).
Số giờ làm việc trong ngày của máy loại 1 là 3x + y.
Số giờ làm việc trong ngày của máy loại 2 là x + y.
Vì máy loại 1 làm việc không quá 6 giờ một ngày, máy loại 2 làm việc không quá 4 giờ 1 ngày nên ta có hệ phương trình
Miền nghiệm của hệ phương trình là miền tứ giác không bị gạch trong hình vẽ.
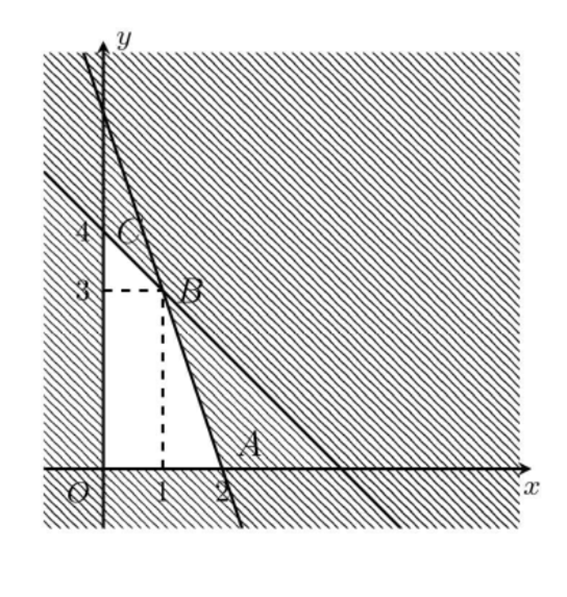
Ta có:
F(0; 0) = 0
F(2; 0) = 4
F(1; 3) = 6,8
F(0; 4) = 6,4
Do đó F(x; y) lớn nhất khi (x; y) = (1; 3).
Vậy để thu được lãi lớn nhất phải sản xuất 1 tấn sản phẩm loại A và 3 tấn sản phẩm loại B.
Câu 8:
13/07/2024Một công ty cho thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có hai loại xe A và B trong đó loại xe A có 10 chiếc và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi xe loại A có thể chở tối đa 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là ít nhất ?
Xem đáp án
Đáp án đúng là: C
Gọi x, y lần lượt là số xe loại A và B cần thuê. Khi đó số tiền cần bỏ ra để thuê xe là F(x; y) = 4x + 3y. Ta có x xe loại A sẽ chở được 20x và 0,6x tấn hàng; y xe loại B sẽ chở được 10y người và 1,5y tấn hàng. Suy ra x xe loại A và y xe loại B sẽ chở được 20x + 10y người và 0,6x + 1,5y tấn hàng.
Ta có hệ bất phương trình sau:
Miền nghiệm của hệ trên là miền tứ giác màu trắng trong hình vẽ.
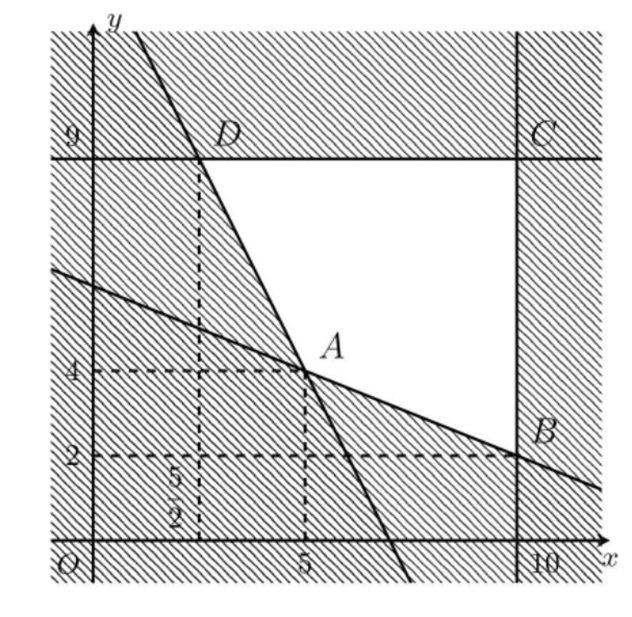
Ta có:
F(5; 4) = 32
F(10; 2) = 46
F(10; 9) = 67
F = 37
Do đó, F(x; y) nhỏ nhất khi (x; y) = (5; 4).
Vây để chi phí vận chuyển thấp nhất cần thuê 5 xe loại A và 4 xe loại B.
Câu 9:
20/07/2024Một nông dân định trồng cà chua và cà pháo trên diện tích 7 ha. Nếu trồng cà chua thì cần 10 công và thu 1 000 000 đồng trên diện tích mỗi ha, nếu trồng cà pháo thì cần 20 công và thu 2 000 000 đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được nhiều tiền nhất biết rằng tổng số công không quá 100 ?
Xem đáp án
Số ha cà chua và cà pháo mà hộ nông dân này trồng lần lượt là x và y (x, y ≥ 0).
Lợi nhuận thu được là F(x; y) = 1 000 000x + 2 000 000y (đồng).
Tổng số công dùng để trồng x ha cà chua và y ha cà pháo là 10x + 20y.
Ta có hệ bất phương trình:
Miền nghiệm của hệ bất phương trình trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên).
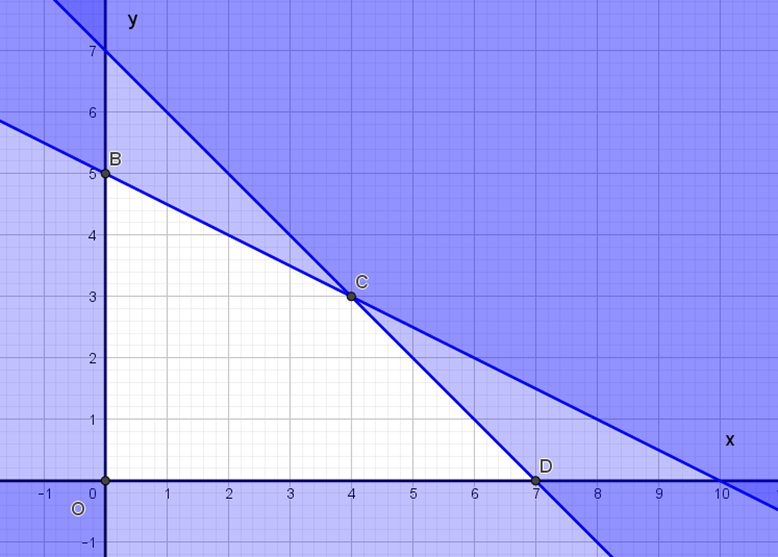
F(x; y) đạt giá trị lớn nhất khi (x; y) là tọa độ của một trong các đỉnh của tứ giác
Ta có:
F(0; 0) = 0
F(0; 5) = 10 000 000
F(4; 3) = 10 000 000
F(7; 0) = 7 000 000
Suy ra F(x; y) lớn nhất khi (x; y) = (0; 5) hoặc (x; y) = (4; 3) tức là hộ nông dân này cần phải trồng 0 ha cà chua và 5 ha cà pháo hoặc 4 ha cà chua hoặc 3 ha cà pháo thì sẽ thu về lợi nhuận lớn nhất.
Câu 10:
13/07/2024Một nông dân định chăn nuôi gà và lợn trên diện tích 20 mét vuông. Nếu nuôi lợn thì cần 40 công và thu 5 000 000 đồng trên diện tích mỗi mét vuông, nếu nuôi gà thì cần 20 công và thu 2 000 000 đồng trên diện tích mỗi mét vuông. Hỏi cần nuôi mỗi loài vật trên với diện tích là bao nhiêu để thu được nhiều tiền nhất biết rằng tổng số công không quá 200 ?
Xem đáp án
Đáp án đúng là: B
Số mét vuông nuôi lợn và nuôi gà mà hộ nông dân này nuôi lần lượt là x và y (x, y ≥ 0).
Lợi nhuận thu được là F(x; y) = 5 000 000x + 2 000 000y (đồng).
Tổng số công dùng để nuôi x mét vuông lợn và y mét vuông gà là 40x + 20y.
Ta có hệ bất phương trình:
Miền nghiệm của hệ bất phương trình trên là miền tứ giác không bị gạch chéo trong hình vẽ (kể cả biên).
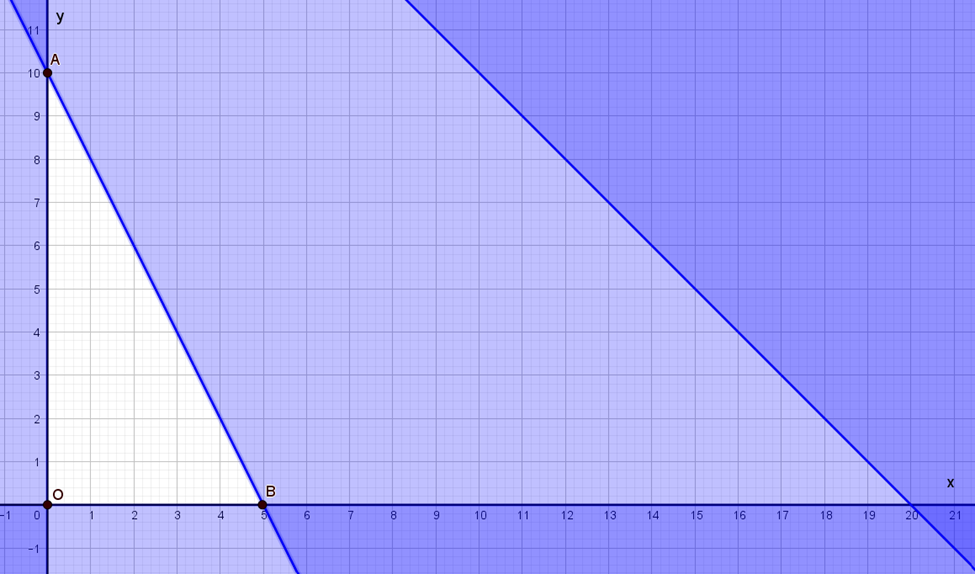
F(x; y) đạt giá trị lớn nhất khi (x; y) là tọa độ của một trong các đỉnh của tam giác.
Ta có:
F(0; 0) = 0
F(5; 0) = 25 000 000
F(0; 10) = 20 000 000
Suy ra F(x; y) lớn nhất khi (x; y) = (5; 0) tức là hộ nông dân này cần dùng 5 mét vuông nuôi lợn và 0 mét vuông nuôi gà thì sẽ thu về lợi nhuận lớn nhất.