Trắc nghiệm Toán 10 (có đáp án): Bài tập ôn tập chương 3
Trắc nghiệm Toán 10 (có đáp án): Bài tập ôn tập chương 3
-
252 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
13/07/2024Số nghiệm của phương trình 2x+2√x+2=−x2+2√x+2 là:
 Xem đáp án
Xem đáp án
Điều kiện: x > -2
2x+2√x+2=−x2+2√x+2
⇔2x=−x2⇔x(x+2)=0⇔[x=0x=−2 (loai)
Kết hợp với điều kiện ta được x = 0 là nghiệm duy nhất
Đáp án cần chọn là: B
Câu 2:
23/07/2024Nghiệm của phương trình √2x−7=1 là:
 Xem đáp án
Xem đáp án
Điều kiện: x≥72
√2x−7=1⇒2x−7=1⇔x=4
Kết hợp với điều kiện ta được x = 4 là nghiệm duy nhất
Đáp án cần chọn là: C
Câu 3:
21/07/2024Nghiệm của phương trình 3x+3x2−1+4x−1=3 là:
 Xem đáp án
Xem đáp án
Điều kiện: x≠±1
3x+3x2−1+4x−1=3⇒3x+3+4(x+1)=3(x2−1)⇔3x2−7x−10=0⇔[x=−1 (ktm)x=103 (tm)
Nên x=103 là nghiệm duy nhất
Đáp án cần chọn là: C
Câu 4:
23/07/2024Tập xác định của phương trình √3x+5x2+1=2√2−x là:
 Xem đáp án
Xem đáp án
Điều kiện xác định {3x+5≥02−x>0⇔{x≥−53x<2⇔−53≤x<2
Đáp án cần chọn là: A
Câu 5:
21/07/2024Điều kiện xác định của phương trình √x+2x=2x2+3x−4 là
 Xem đáp án
Xem đáp án
Điều kiện xác định {x+2≥0x≠0x2+3x−4≠0⇔{x≥−2x≠1x≠0x≠−4⇔x∈[-2;+∞)\
Đáp án cần chọn là: C
Câu 7:
18/07/2024Gọi n là số các giá trị của tham số m để phương trình vô số nghiệm. Thế thì n là:
 Xem đáp án
Xem đáp án
Ta có:
Phương trình (∗) vô số nghiệm
Đáp án cần chọn là: B
Câu 8:
12/07/2024Phương trình có hai nghiệm khi:
 Xem đáp án
Xem đáp án
Phương trình có hai nghiệm khi
Đáp án cần chọn là: D
Câu 9:
20/07/2024Số nghiệm phương trình: là:
 Xem đáp án
Xem đáp án
Đặt , phương trình trở thành:
Phương trình (*) có hệ số phương trình có hai nghiệm trái dấu
Vậy phương trình đã cho có 2 nghiệm phân biệt
Đáp án cần chọn là: D
Câu 10:
23/07/2024Gọi là các nghiệm của phương trình: . Khi đó giá trị của biểu thức là:
 Xem đáp án
Xem đáp án
Ta gọi hai nghiệm của phương trình đã cho là . Theo hệ thức Vi-et ta có:
Đáp án cần chọn là: C
Câu 11:
23/07/2024Phương trình có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Phương trình cho
Nên phương trình có vô số nghiệm
Đáp án cần chọn là: D
Câu 13:
22/07/2024Phương trình có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
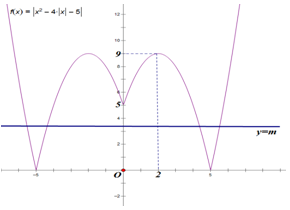
Ta có:
Số nghiệm của phương trình là số giao điểm của hàm số và đường thẳng
Để vẽ đồ thị hàm số ta vẽ đồ thị hàm số , sau đó suy ra đồ thị hàm số bằng cách: bỏ đi phần đồ thị bên trái trục Oy, lấy đối xứng phần đồ thị nằm bên phải trục Oy qua Oy.
Từ đồ thị hàm số ta suy ra đồ thị hàm số bằng cách lấy đối xứng toàn bộ phần đồ thị phía dưới trục Ox qua Ox sau đó bỏ đi phần đồ thị phía dưới trục Ox.
Dựa vào đồ thị thì đường thẳng cắt đồ thị hàm số tại hai điểm phân biệt nên phương trình đã cho có hai nghiệm phân biệt.
Đáp án cần chọn là: A
Câu 14:
23/07/2024Phương trình sau đây có bao nhiêu nghiệm:
 Xem đáp án
Xem đáp án
Đặt
Ta có phương trình
Ta thấy phương trình (2) có
Suy ra phương trình vô nghiệm
Đáp án cần chọn là: A
Câu 16:
12/07/2024Nghiệm của hệ phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện:
Đặt thì:
Đáp án cần chọn là: A
Câu 17:
12/07/2024Số nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện: . Ta có phương trình
Vậy phương trình đã cho có hai nghiệm
Đáp án cần chọn là: D
Câu 18:
12/07/2024Tổng các lập phương hai nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Phương trình có tổng lập phương các nghiệm là
Đáp án cần chọn là: D
Câu 19:
15/07/2024Số nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Ta có:
Phương trình vô nghiệm
Phương trình . Do đó phương trình cho có 2 nghiệm
Đáp án cần chọn là: B
Câu 20:
21/07/2024Phương trình có bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Điều kiện: x < 2
PT
Đáp án cần chọn là: A
Câu 21:
21/07/2024Phương trình có nghiệm thỏa mãn:
 Xem đáp án
Xem đáp án
Điều kiện:
Vì nên
Kết hợp điều kiện phương trình có nghiệm duy nhất x = 3
Đáp án cần chọn là: C
Câu 22:
23/07/2024Số nghiệm của hệ phương trình
 Xem đáp án
Xem đáp án
Nhận thấy x = y = 0 không là nghiệm của hệ phương trình đã cho nên ta có:
Vậy hệ đã cho có bốn nghiệm
Đáp án cần chọn là: A
Câu 23:
14/07/2024Tìm m để phương trình có hai nghiệm phân biệt sao cho đạt giá trị nhỏ nhất
 Xem đáp án
Xem đáp án
PT có 2 nghiệm phân biệt
Theo Vi-et ta có:
Ta có:
Dấu ‘=’ xảy ra khi (thỏa mãn (*))
Vậy đạt giá trị nhỏ nhất khi
Đáp án cần chọn là: C
Câu 24:
23/07/2024Tìm m để phương trình có hai nghiệm thỏa mãn:
 Xem đáp án
Xem đáp án
Phương trình có hai nghiệm
Theo Vi-et ta có:
Ta có: (thỏa mãn (*))
Đáp án cần chọn là: B
Câu 25:
21/07/2024Cho phương trình sau . Chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
Điều kiện:
Vậy phương trình vô nghiệm
Đáp án cần chọn là: B
