Trắc nghiệm Toán 10 Bài 2. Giải bất phương trình bậc hai một ẩn có đáp án
Trắc nghiệm Toán 10 Bài 2. Giải bất phương trình bậc hai một ẩn có đáp án
-
333 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Tập nghiệm của bất phương trình x2 + 4x + 4 > 0 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tam thức bậc hai f(x) = x2 + 4x + 4 có ∆ = 0; nghiệm là x = – 2 và a = 1 > 0
Ta có bảng xét dấu

Từ bảng xét dấu ta có x2 + 4x + 4 > 0 với mọi x \( \in \) (– ∞; – 2)\( \cup \)(– 2; + ∞).
Câu 2:
19/07/2024Tập nghiệm của bất phương trình x2 – 1 > 0 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Tam thức bậc hai f(x) = x2 – 1 có ∆ = 4 > 0; hai nghiệm phân biệt là x = – 1; x = 1 và a = 1 > 0
Ta có bảng xét dấu

Từ bảng xét dấu ta có x2 – 1 > 0 với mọi x \( \in \) (–∞; –1)\( \cup \)(1; +∞).
Câu 3:
13/07/2024Tập nghiệm của bất phương trình x2 – x – 6 ≤ 0 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tam thức bậc hai f(x) = x2 – x – 6 có ∆ = 25 > 0; hai nghiệm phân biệt là x = – 2; x = 3 và a = 1 > 0
Ta có bảng xét dấu
|
x |
–∞ –2 3 + ∞ |
|
f(x) |
+ 0 – 0 + |
Từ bảng xét dấu ta có x2 – x – 6 ≤ 0 với mọi x \( \in \) [– 2; 3].
Câu 4:
16/07/2024Tập ngiệm của bất phương trình x(x + 5) ≤ 2(x2 + 2) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: x(x + 5) ≤ 2(x2 + 2) \( \Leftrightarrow \) x2 – 5x + 4 ≥ 0.
Xét tam thức f(x) = x2 – 5x + 4 có ∆ = 9 > 0, hai nghiệm phân biệt là x = 1; x = 4 và a = 1 > 0.
Ta có bảng xét dấu :
|
x |
- ∞ 1 4 + ∞ |
|
f(x) |
+ 0 – 0 + |
Từ bảng xét dấu ta có tập nghiệm của bất phương trình là (– ∞; 1]\( \cup \)[4; + ∞).
Câu 5:
20/07/2024Tập nghiệm của bất phương trình 2x2 – 7x – 15 ≥ 0 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét tam thức f(x) = 2x2 – 7x – 15 có ∆ = 169 > 0, hai nghiệm phân biệt là x = 5; x = \( - \frac{3}{2}\) và a = 2 > 0.
Ta có bảng xét dấu :
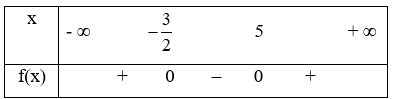
Từ bảng xét dấu ta có tập nghiệm của bất phương trình là \[\left( {--\infty ; - \frac{3}{2}}
Câu 6:
21/07/2024Tìm tất cả các giá trị của m để bất phương trình mx2 – x + m ≥ 0 với mọi x \( \in \) ℝ
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đặt f(x) = mx2 – x + m là tam thức bậc hai với a = m, b = – 1 và c = m
Với m = 0 thì f(x) = – x , f(x) ≥ 0 ⇔ – x ≥ 0 ⇔ x ≤ 0. Vậy m = 0 không thỏa mãn.
Với m ≠ 0 thì f(x) = mx2 – x + m ≥ 0 với mọi x \( \in \) ℝ \( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\Delta = {1^2} - 4.m.m \le 0\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\1 - 4{m^2} \le 0\end{array} \right.\)
Xét f(m) = 1 – 4m2 có ∆ = 16 > 0, hai nghiệm phân biệt là x = \( - \frac{1}{2}\); x = \(\frac{1}{2}\) và a = – 4 < 0. Ta có bảng xét dấu
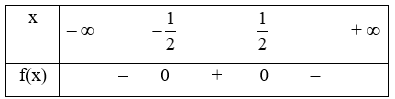
Từ bảng xét dấu ta có để 1 – 4m2 ≤ 0 thì m\( \in \left( { - \infty ; - \frac{1}{2}} \right] \cup \left[ {\frac{1}{2}; + \infty } \right)\)
Vậy để mx2 – x + m ≥ 0 với mọi x \( \in \) ℝ \( \Leftrightarrow \) \(\left\{ \begin{array}{l}m > 0\\\left[ \begin{array}{l}m \le - \frac{1}{2}\\m \ge \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow m \ge \frac{1}{2}\)
Câu 7:
20/07/2024Tìm tất cả các giá trị của m để bất phương trình x2 – x + m ≤ 0 vô nghiệm?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Bất phương trình x2 – x + m ≤ 0 vô nghiệm \( \Leftrightarrow \) x2 – x + m > 0 với mọi x \( \in \) ℝ
\( \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\\Delta = {\left( { - 1} \right)^2} - 4.1.m < 0\end{array} \right.\)\( \Leftrightarrow m > \frac{1}{4}\)
Câu 8:
21/07/2024Gọi S là tập nghiệm của bất phương trình x2 – 8x + 7 ≥ 0. Trong các tập hợp sau, tập nào không là tập con của S?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét tam thức f(x) = x2 – 8x + 7 có ∆ = 36 > 0, hai nghiệm phân biệt là x = 1; x = 7 và a = 1 > 0
Ta có bảng xét dấu
|
x |
–∞ 1 7 + ∞ |
|
f(x) |
+ 0 – 0 + |
Từ bảng xét dấu ta có tập nghiệm của bất phương trình là S = (– ∞; 1]\( \cup \)[7; + ∞);
Vậy tập không phải là con của tập S là [6; + ∞).
Câu 9:
23/07/2024Các giá trị m để bất phương trình x2 – (m + 2)x + 8m + 1 < 0 luôn có nghiệm
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Để bất phương trình x2 – (m + 2)x + 8m + 1 < 0 luôn có nghiệm khi và chỉ khi ∆ ≥ 0
\( \Leftrightarrow \) (m + 2)2 – 4(8m + 1) ≥ 0 \( \Leftrightarrow \) m2 – 28m ≥ 0
Xét f(m) = m2 – 28m có ∆ = 784 > 0 có hai nghiệm là m = 0; m = 28 và a = 1 > 0. Ta có bảng xét dấu
|
m |
–∞ 0 28 + ∞ |
|
f(m) |
+ 0 – 0 + |
Từ bảng xét dấu ta có để m2 – 28m ≥ 0 thì m ≤ 0 hoặc m ≥ 28.
Vậy với m ≤ 0 hoặc m ≥ 28 thì phương trình đã cho có nghiệm.
Câu 10:
22/07/2024Tìm m để x2 – 2(2m – 3)x + 4m – 3 > 0 với mọi x \( \in \) ℝ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì a = 1 > 0 nên để x2 – 2(2m – 3)x + 4m – 3 > 0 với mọi x \( \in \) ℝ thì ∆’ < 0
Ta có ∆’ = (2m – 3)2 – 1.(4m – 3) = 4m2 – 16m + 12 < 0
Xét f(m) = 4m2 – 16m + 12 có ∆ = 64 > 0, hai nghiệm phân biệt là m = 1; m = 3 và a = 4 > 0. Ta có bảng xét dấu
|
m |
–∞ 1 3 + ∞ |
|
f(m) |
+ 0 – 0 + |
Từ bảng xét dấu ta có để 4m2 – 16m + 12 < 0 thi 1 < m < 3.
Vậy với 1 < m < 3 thì x2 – 2(2m – 3)x + 4m – 3 > 0.
Câu 11:
13/07/2024Tìm m để – 2x2 + (m + 2)x + m – 4 < 0 với mọi x \( \in \) ℝ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Để –2x2 + (m + 2)x + m – 4 < 0 với mọi x \( \in \) ℝ\[ \Leftrightarrow \left\{ \begin{array}{l}\Delta < 0\\a < 0\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}a = - 2 < 0\\{\left( {m + 2} \right)^2} + 8\left( {m - 4} \right) < 0\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}a = - 2 < 0\\{m^2} + 12m - 28 < 0\end{array} \right.\]
Xét f(m) = m2 + 12m – 28 có ∆ = 256 > 0, hai nghiệm phân biệt là m = 2; m = –14 và a = – 2 < 0
Ta có bảng xét dấu
|
m |
- ∞ - 14 2 + ∞ |
|
f(m) |
+ 0 - 0 + |
Từ bảng xét dấu ta có: Để m2 + 12m – 28 < 0 thì – 14 < m < 2.
Vậy với – 14 < m < 2 thì – 2x2 + (m + 2)x + m – 4 < 0 với mọi x ∈ ℝ.
Câu 12:
20/07/2024Xác định m để (m2 + 2)x2 – 2(m – 2)x + 2 > 0 với mọi x \( \in \) ℝ
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có (m2 + 2)x2 – 2(m – 2)x + 2 > 0 với mọi x \( \in \) ℝ \( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta < 0\end{array} \right.\)
\[ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 2 > 0\\ - {m^2} - 4m < 0\end{array} \right.\]
Xét f(m) = – m2 – 4m có ∆ = 16 > 0, hai nghiệm phân biệt là m = 0; m = – 4 và a = – 1 < 0. Ta có bảng xét dấu
|
m |
– ∞ – 4 0 + ∞ |
|
f(m) |
– 0 + 0 – |
Từ bản xét dấu ta có để – m2 – 4m < 0 thì m < – 4 hoặc m > 0.
Vậy với m < – 4 hoặc m > 0 thì (m2 + 2)x2 – 2(m – 2)x + 2 > 0 với mọi x \( \in \) ℝ.
Câu 13:
22/07/2024Cho bất phương trình x2 – (2m + 2)x + m2 + 2m < 0. Tìm m để bất phương trình nghiệm đúng với mọi x thuộc đoạn [0; 1]
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: a = 1 > 0. Do đó, x2 – (2m + 2)x + m2 + 2m < 0 mọi x thuộc đoạn [0; 1]
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{x_1} < 0 < 1 < {x_2}\end{array} \right. \Leftrightarrow \)\(\left\{ \begin{array}{l}{\left[ { - \left( {m + 1} \right)} \right]^2} - \left( {{m^2} + 2m} \right) > 0\\af\left( 0 \right) < 0\\af\left( 1 \right) < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\{m^2} + 2m < 0\\{m^2} - 1 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - 2 < m < 0\\ - 1 < m < 1\end{array} \right.\)\( \Leftrightarrow \) –1 < m < 0.
Vậy với –1 < m < 0 thì x2 – (2m + 2)x + m2 + 2m < 0 mọi x thuộc đoạn [0; 1].
Câu 14:
18/07/2024Cho phương trình x2 – 2x – m = 0. Tìm tất cả các giá trị của m để phương trình có 2 nghiệm thỏa mãn x1 < x2 < 2.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Phương trình có hai nghiệm phân biệt ∆’ > 0 \( \Leftrightarrow \) (– 1)2 + m > 0 \( \Leftrightarrow \) m > – 1.
Để phương trình có hai nghiệm thỏa mãn x1 < x2 < 2.
\( \Leftrightarrow \left\{ \begin{array}{l}{x_1} - 2 + {x_2} - 2 < 0\\\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} - 4 < 0\\{x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) + 4 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}2 - 4 < 0\\ - m - 2.2 + 4 > 0\end{array} \right.\)
\( \Leftrightarrow \) m < 0.
Kết hợp với điều kiện ta được: – 1 < m < 0.
Câu 15:
21/07/2024Cho bất phương trình mx2 – (2m – 1)x + m + 1 < 0(1). Tìm tất cả các giá trị thực của tham số m để bất phương trình (1) vô nghiệm.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đặt f(x) = mx2 – (2m – 1)x + m + 1.
Ta có f(x) < 0 vô nghiệm \( \Leftrightarrow f\left( x \right) \ge 0\,\,\forall x \in \mathbb{R}\) \( \Leftrightarrow \) f(x) ≥ 0 với mọi x \( \in \) ℝ
Xét m = 0 khi đó f(x) = x + 1 nên m = 0 không thoả mãn.
Xét m ≠ 0\( \Leftrightarrow \) f(x) ≥ 0 với mọi x \( \in \) ℝ \( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\Delta = - 8m + 1 \le 0\end{array} \right.\)\( \Leftrightarrow m \ge \frac{1}{8}\).
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 2. Giải bất phương trình bậc hai một ẩn có đáp án (332 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 2. Giải phương trình bậc hai một ẩn (Phần 2) có đáp án (504 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 CTST Bài tập cuối chương 7 (Phần 2) có đáp án (704 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 1. Dấu của tam thức bậc hai (Phần 2) có đáp án (676 lượt thi)
- Trắc nghiệm Toán 10 CTST Bài 3. Phương trình quy về phương trình bậc hai (Phần 2) có đáp án (409 lượt thi)
- Trắc nghiệm Toán 10 Bài 1. Dấu của tam thức bậc hai có đáp án (298 lượt thi)
- Trắc nghiệm Toán 10 Bài tập cuối chương 7 có đáp án (225 lượt thi)
- Trắc nghiệm Toán 10 Bài 3. Phương trình quy về phương trình bậc hai có đáp án (203 lượt thi)
