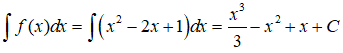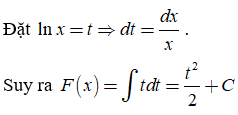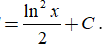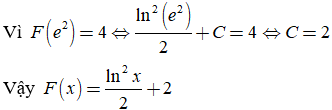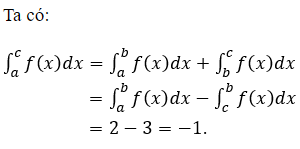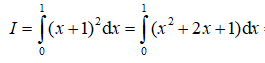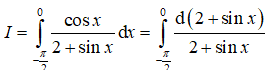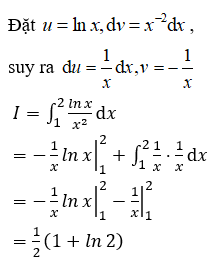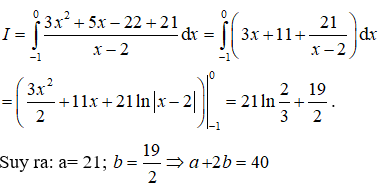Top 8 Đề kiểm tra Toán 12 Chương 3 Giải tích có đáp án
Đề kiểm tra 15 phút Toán 12 Chương 3 Giải tích có đáp án (Đề 6)
-
2079 lượt thi
-
20 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 2:
21/07/2024F(x) là một nguyên hàm của hàm số , biết rằng F(1) = 1. F(x) là biểu thức nào sau đây
 Xem đáp án
Xem đáp án
Chọn D.
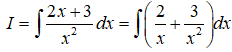
![]()
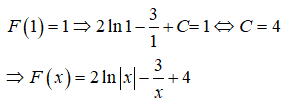
Câu 4:
23/07/2024Một nguyên hàm của hàm số là:
 Xem đáp án
Xem đáp án
Chọn C.
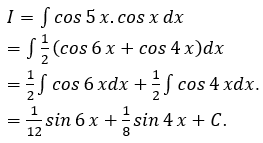
Cho C = 0, ta được 1 nguyên hàm của hàm số đã cho là:
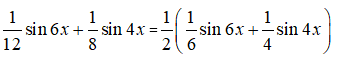
Câu 6:
17/07/2024Một nguyên hàm của là kết quả nào sau đây, biết nguyên hàm này triệt tiêu khi x = 1?
 Xem đáp án
Xem đáp án
Chọn D.

Theo công thức tính nguyên hàm từng phần, ta có:
![]()
![]()
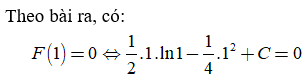
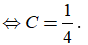
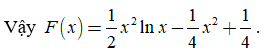
Câu 7:
17/07/2024Xét hàm số f liên tục trên R và các số thực a, b, c tùy ý. Trong các khẳng định sau, khẳng định nào sai?
 Xem đáp án
Xem đáp án
Chọn C
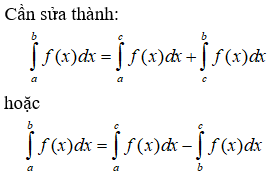
Câu 10:
20/07/2024Tích phân: bằng
 Xem đáp án
Xem đáp án
Chọn A.
Đặt t = x + 1⇒ dt = dx. Đổi cận: x = 0 ⇒ t = 1; x = 1 ⇒ t = 2

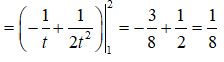
Câu 14:
20/07/2024Diện tích hình phẳng được giới hạn bởi các đường và đường thẳng x = -2 là:
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = x3 + 3x và y = -x là: x3 + 4x = 0 ⇔ x = 0
Ta có: x3 + 4x ≤ 0, ∀ x ∈ [-2;0].
Do đó:
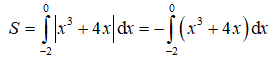
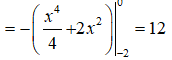
Câu 15:
19/07/2024Cho hàm số f(x) liên tục trên R và với mọi x ∈ R. Giá trị của tích phân là
 Xem đáp án
Xem đáp án
Chọn B.
Đặt t = - x suy ra: dt = -dx
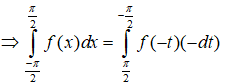
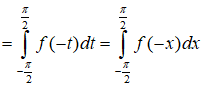
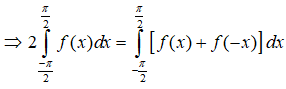
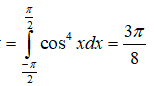

Câu 16:
20/07/2024Diện tích hình phẳng giới hạn bởi có kết quả là
 Xem đáp án
Xem đáp án
Chọn B.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = 2x - x2 và y = -x là :
Câu 17:
22/07/2024Thể tích của khối tròn xoay được giới hạn bởi đồ thị hàm số liên tục trên đoạn [a;b] trục Ox và hai đường thẳng quay quanh trục Ox, có công thức là:
 Xem đáp án
Xem đáp án
Chọn B.
Áp dụng công thức tính thể tích khối tròn xoay: giới hạn bởi đồ thị hàm số y = f(x), trục Ox, x = a, x = b khi quay xung quanh trục Ox ta có:
Câu 20:
20/07/2024Hình (S) giới hạn bởi Tính thể tích khối tròn xoay khi quay hình (S) quanh trục Ox.
 Xem đáp án
Xem đáp án
Chọn C.
Phương trình hoành độ giao điểm:
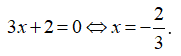
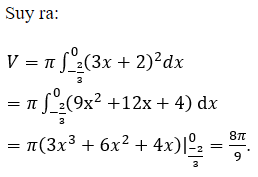
Bài thi liên quan
-
Đề kiểm tra 15 phút Toán 12 Chương 3 Giải tích có đáp án (Đề 1)
-
10 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 3 Giải tích có đáp án (Đề 2)
-
10 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 3 Giải tích có đáp án (Đề 3)
-
8 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 3 Giải tích có đáp án (Đề 4)
-
8 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 3 Giải tích có đáp án (Đề 5)
-
20 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 3 Giải tích có đáp án (Đề 7)
-
20 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 3 Giải tích có đáp án (Đề 8)
-
20 câu hỏi
-
20 phút
-
Có thể bạn quan tâm
- Đề kiểm tra 1 tiết Giải tích 12 Chương 3 có đáp án (384 lượt thi)
- Đề kiểm tra 1 tiết Giải tích 12 Chương 4 có đáp án (296 lượt thi)
- Đề thi Học kì 2 Giải tích 12 có đáp án (314 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 3 Giải tích có đáp án (2078 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 4 Giải tích có đáp án (1668 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 3 Hình học có đáp án (2194 lượt thi)
Các bài thi hot trong chương
- Top 8 Đề kiểm tra Toán 12 Chương 1 Hình học có đáp án (3453 lượt thi)
- Top 4 Đề thi Toán lớp 12 Học kì 1 chọn lọc, có đáp án (2868 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 2 Hình học có đáp án (2461 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 2 Giải tích có đáp án (2228 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 1 Giải tích có đáp án (2222 lượt thi)
- Đề kiểm tra 1 tiết Giải tích 12 Chương 1 có đáp án (415 lượt thi)
- Đề kiểm tra 1 tiết Giải tích 12 chương 2 có đáp án (288 lượt thi)