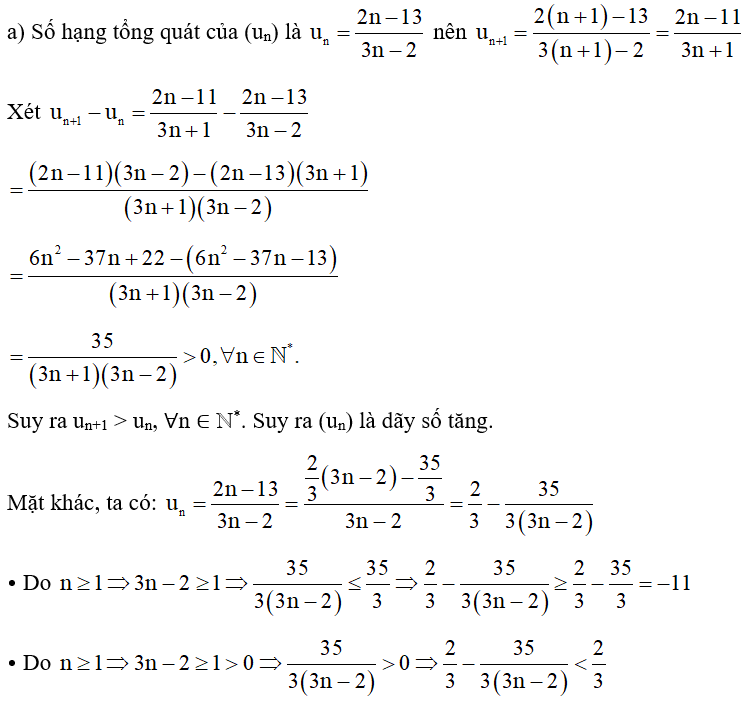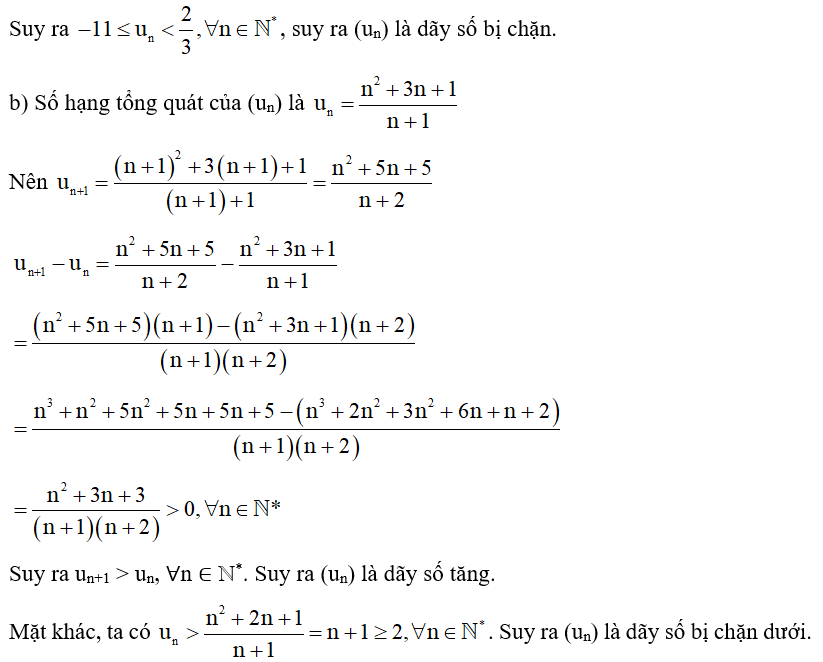Giải SBT Toán 11 CTST Bài 1. Dãy số
-
60 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
12/07/2024Cho dãy số (un) với un=n+12n+1. Số 815 là số hạng thứ bao nhiêu của dãy số?
 Xem đáp án
Xem đáp án
Ta có: n+12n+1=815
Suy ra 15(n + 1) = 8(2n + 1), hay 15n + 15 = 16n + 8, nên n = 7.
Vậy 815 là số hạng thứ bảy của dãy số.
Câu 2:
23/07/2024Dự đoán công thức số hạng tổng quát của dãy số (un), biết {u1=−2un+1=−2−1un.
 Xem đáp án
Xem đáp án
Bốn số hạng đầu tiên của dãy un là:
u1 = ‒2;
u2=−2−1−2=−32;
u3=−2−1−32=−43;
u4=−2−1−43=−54;
Ta dự đoán được số hạng tổng quát của dãy số (un) là un=−n+1n.
Câu 3:
06/07/2024Cho dãy số (un) xác định bởi {u1=4un+1=un+n(n≥1). Tìm số hạng thứ năm của dãy số đó.
 Xem đáp án
Xem đáp án
Ta có:
u2 = u1 + 1 = 4 + 1 = 5;
u3 = u2 + 2 = 5 + 2 = 7;
u4 = u3 + 3 = 7 + 3 = 10
Do đó, số hạng thứ năm của dãy số là u5 = u4 + 4 = 10 + 4 = 14.
Câu 4:
06/07/2024Xét tính bị chặn của dãy số (un) với un = (‒1)n.
 Xem đáp án
Xem đáp án
Ta có:
u1 = (‒1)1 = −1; u3 = (‒1)3 = −1; …
u2 = (‒1)2 = 1; u4 = (‒1)4 = 1; …
Do đó ‒1 ≤ un ≤ 1, suy ra (un) là dãy bị chặn.
Câu 6:
06/07/2024Xét tính tăng, giảm của các dãy số (un) cho bởi số hạng tổng quát un sau:
a) un=n−√n2−1;
b) un=n+(−1)nn2;
c) un=3n−12n.
 Xem đáp án
Xem đáp án
a) Ta có:
Suy ra là dãy số giảm.
b) Xét ta có: , suy ra .
Do đó, (un) là dãy số không tăng, không giảm.
c) Ta có .
Do đó, (un) là dãy số tăng.
Câu 7:
06/07/2024Xét tính tăng, giảm và bị chặn của dãy số (un) với
 Xem đáp án
Xem đáp án
Ta có: .
Suy ra . Suy ra (un) là dãy số tăng.
Do , suy ra 1 < un < 2, ∀n ∈ ℕ*.
Suy ra (un) là dãy số bị chặn.