Cách Phân tích một số ra thừa số nguyên tố cực hay, có lời giải
-
236 lượt thi
-
14 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Gọi P là tập hợp số nguyên tố. Điền kí hiệu hoặc thích hợp vào chỗ chấm:
43……P
93……P
15…….N
P…..N
Xem đáp án
43 ∈ P
93 ∉ P
15 ∈ N
P ⊂ N
Câu 2:
22/07/2024a) Tìm số tự nhiên k để 3.k là số nguyên tố
Xem đáp án
a) Để 3.k là số nguyên tố thì 3.k chỉ có ước là 3 và 1 nên k = 1
Câu 3:
22/07/2024b) Thay chữ số vào dấu * để được số nguyên tố: 5* ; 9*
Xem đáp án
b) 59 là số nguyên tố vậy * = 9
97 là số nguyên tố vậy * = 7
Câu 4:
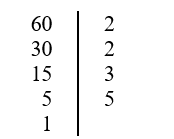
22/07/2024Phân tích số 60 ra thừa số nguyên tố, từ đó tìm tập hợp Ư(60) và đếm xem 60 có bao nhiêu ước số?
Xem đáp án
Suy ra 60= 2.2.3.5 =22.31.51.
Như vậy, số 60 đã được phân tích ra thừa số nguyên tố.
Từ ví dụ trên ta có một số nhận xét sau:
• Khi viết, các thừa số nguyên tố được sắp xếp theo thứ tự từ nhỏ đến lớn.
• Ư(60) = {1;2;3;4;5;6;10;12;15;20;30;60}
• Số 60 có tất cả (2+1)(1+1)(1+1) = 3.2.2 = 12 ước số
Câu 5:
22/07/2024Trong các số sau, số nào là số nguyên tố: 2, 4, 13, 19, 25, 31
Xem đáp án
Đáp án: C
A. 2, 4, 13, 19, 31 → Sai vì 4 ⋮ 2; số 4 không phải là số nguyên tố vì ngoài 1 và 4 thì 4 còn có ước là 2
B. 4, 13, 19, 25, 31 tương tự câu a ta có 4 là hợp số; và 25 không phải số nguyên tố vì 25 ngoài 1 và 25 thì 25 còn có ước là 5.
C. 2, 13, 19, 31 → Đúng
D. 2, 4, 13, 19 → Sai vì 4 ⋮ 2
Câu 6:
22/07/2024Khẳng định nào sau đây là sai?
Xem đáp án
Đáp án: B
A. Số 2 là số nguyên tố bé nhất → Đúng
B. Mọi số nguyên tố đều là số lẻ → Sai vì có 2 là số nguyên tố chẵn duy nhất
C. Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước → Đúng
D. Có 2 số tự nhiên liên tiếp là số nguyên tố → Đúng là 2 và 3
Câu 7:
22/07/2024Tìm số tự nhiên a sao cho 6 - a là số nguyên tố?
Xem đáp án
Đáp án: A
A. a = 1, a = 3
Khi a = 1
6 – a = 6 - 1 = 5 là số nguyên tố
Khi a = 3
6 – 3 = 3 là số nguyên tố
B. a = 1; a = 5. Khi a = 5; 6 - a = 6 - 5 = 1 không phải số nguyên tố
C. a = 3, a = 7. Khi a = 7; 6 – 7 phép tính không thực hiện được
D. a = 1, a = 7. Tương tự câu C
Câu 8:
22/07/2024Ba số tự nhiên lẻ liên tiếp đều là số nguyên tố là?
Xem đáp án
Đáp án: B
A. 1, 3, 5 → Sai vì 1 không là số nguyên tố
B. 3, 5, 7 → Đúng
C. 5, 7, 9 → Sai vì 9 không phải là số nguyên tố
D. 7, 9, 11 → Sai vì 9 không phải là số nguyên tố
Câu 9:
22/07/2024Chọn phát biểu sai:
Xem đáp án
Đáp án: D
A. Số nguyên tố nhỏ hơn 10 là 2, 3, 5, 7 → Đúng
B. 2 là số nguyên tố chẵn duy nhất → Đúng
C. Số 0 không là số nguyên tố cũng không là hợp số → Đúng
D. Số 1 là số nguyên tố bé nhất → Sai vì số 2 là số nguyên tố nhỏ nhất
Câu 10:
23/07/2024Khẳng định nào sau đây sai?
Xem đáp án
Đáp án: B
A. 0 và 1 không phải là số nguyên tố cũng không phải là hợp số.Đúng
B. Cho số a > 1, a có 2 ước thì a là hợp số → Sai vì a có 2 ước thì a là số nguyên tố
C. 2 là số nguyên tố chẵn duy nhất → Đúng
D. Số nguyên tố là số tự nhiên lớn hơn 1 mà chỉ có hai ước 1 và chính nó → Đúng
Câu 11:
22/07/2024Khẳng định nào sau đây đúng?
Xem đáp án
Đáp án: B
A. A = {0; 1} là tập hợp số nguyên tố → Sai vì 0 và 1 không phải là số nguyên tố
B. A = {3; 5} là tập hợp số nguyên tố → Đúng
C. A = {1; 3; 5} là tập hợp các hợp số → Sai vì 3;5 là số nguyên tố
D. A = {7; 8} là tập hợp các hợp số → Sai vì 7 là số nguyên tố
Câu 12:
22/07/2024Kết quả của phép tính nào sau đây là số nguyên tố
Xem đáp án
Đáp án: A
A. 15 - 5 + 3 = 13 là số nguyên tố
B. 7.2 + 1 = 15 là hợp số
C. 14.6:4 = 21 là hợp số
D. 6.4 - 12.2 = 0 không phải là hợp số cũng không là số nguyên tố
Câu 13:
22/07/2024Tìm số tự nhiên x để được số nguyên tố x
Xem đáp án
Đáp án: A
A. 7
B. 4
C. 6
D. 9
Để 3x là số nguyên tố thì x = 7 hay số đó là 37
Câu 14:
22/07/2024Cho các số 21; 71; 77; 101. Chọn phát biểu đúng trong các phát biểu sau?
Xem đáp án
Đáp án: B
A. Số 21 là hợp số, các số còn lại là số nguyên tố → Sai vì 77 là hợp số
B. Có hai số nguyên tố và hai số là hợp số trong các số trên → Đúng vì có 21;77 là hợp số
C. Chỉ có một số nguyên tố, còn lại là hợp số → Sai vì có 71; 101 là số nguyên tố
D. Không có số nguyên tố nào trong các số trên → Sai vì 71;101 là số nguyên tố