Bài tập Parabol có đáp án
-
400 lượt thi
-
14 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
15/07/2024Chứng tỏ rằng nếu điểm M(x0; y0) nằm trên parabol (P) thì điểm M'(x0; –y0) cũng nằm trên parabol (P).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
M(x0; y0) thuộc (P) thì
Có nên M'(x0; –y0) cũng thuộc (P).
Câu 2:
18/07/2024Tìm toạ độ tiêu điểm, toạ độ đỉnh, phương trình đường chuẩn và trục đối xứng của các parabol sau:
a) (P1): = 2x;
b) (P2): = x;
c) .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Có 2p = 2, suy ra p = 1.
Toạ độ tiêu điểm của parabol là F (1/2;0)
Toạ độ đỉnh của parabol là O(0; 0).
Phương trình đường chuẩn của parabol là x = -1/2
Trục đối xứng của parabol là trục Ox.
b) Có 2p = 1, suy ra p = 1/2
Toạ độ tiêu điểm của parabol là F(1/4;0)
Toạ độ đỉnh của parabol là O(0; 0).
Phương trình đường chuẩn của parabol là x = -1/4
Trục đối xứng của parabol là trục Ox.
c) Có 2p = 1/5 suy ra p = 1/10
Toạ độ tiêu điểm của parabol là F(1/20;0)
Toạ độ đỉnh của parabol là O(0; 0).
Phương trình đường chuẩn của parabol là x = -1/20
Trục đối xứng của parabol là trục Ox.
Câu 3:
20/07/2024Trong mặt phẳng Oxy, cho điểm A(2; 0) và đường thẳng d: x + 2 = 0. Viết phương trình của đường (L) là tập hợp các tâm J(x; y) của các đường tròn (C) thay đổi nhưng luôn luôn đi qua A và tiếp xúc với d.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Có JA =
Khoảng cách từ J đến d là: d(J; d) = |x + 2|.
Đường tròn (C) luôn đi qua A và tiếp xúc với d => JA = d(J; d)
Vậy (L) là một parabol có phương trình
Câu 4:
30/06/2024Cho điểm M(x; y) trên parabol (P): y2 = 2px (Hình 2). Tính khoảng cách từ điểm M đến tiêu điểm F của (P).
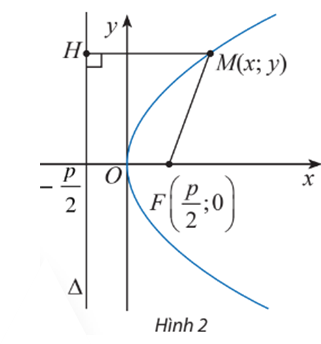
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Vì M thuộc (P) nên = 2px.
Khoảng cách từ điểm M đến tiêu điểm F là: MF =
(vì x + p/2 > 0).
Câu 5:
22/07/2024Tính bán kính qua tiêu của điểm dưới đây trên parabol tương ứng:
a) Điểm M1(1; –4) trên (P1): = 16x;
b) Điểm M2(3; –3) trên (P2): = 3x;
c) Điểm M3(4; 1) trên : .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Có 2p = 16, suy ra p = 8.
Bán kính qua tiêu của M1 là: FM1 = x + p/2 = 1 + 8/2 = 5.
b) Có 2p = 3, suy ra p = 3/2
Bán kính qua tiêu của M2 là: FM2 = x + p/2 = 3 + 3/4 = 15/4
c) Có 2p = 1/4 suy ra p = 1/8
Bán kính qua tiêu của M3 là: FM3 = x + p/2 = 4 + 1/16 = 65/16
Câu 6:
12/07/2024Một cồng có dạng một đường parabol (P). Biết chiều cao của cổng là 7,6 m và khoảng cách giữa hai chân cổng là 9 m. Người ta muốn treo một ngôi sao tại tiêu điểm F của (P) bằng một đoạn dây nối từ đỉnh S của cổng. Tính khoảng cách từ tâm ngôi sao đến đỉnh cổng.

 Xem đáp án
Xem đáp án
Hướng dẫn giải
Chọn hệ trục toạ độ sao cho gốc O trùng với đỉnh của parabol và trục Ox trùng với tâm đối xứng của parabol, đơn vị trên hai trục toạ độ là mét.
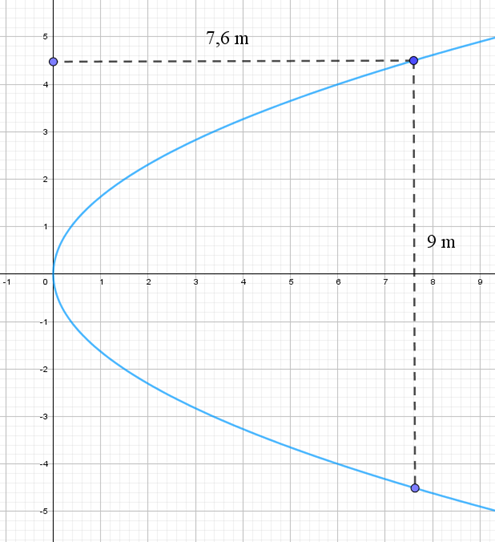
Giả sử parabol có phương trình chính tắc = 2px (p > 0).
Vì chiều cao của cổng là 7,6 m và khoảng cách giữa hai chân cổng là 9 m nên ta có: khi x = 7,6 thì y = 9/2 = 4,5 => 4,52 = 2p . 7,6 => p = 405/304
=> Toạ độ của tâm ngôi sao là F(p/2;0) hay F (405/608;0)
=> Khoảng cách từ tâm ngôi sao đến đỉnh cổng là 405/608 mét.
Câu 7:
16/07/2024Mặt cắt của một chảo ăng-ten có dạng một parabol (P) có phương trình chính tắc = 0,25x. Biết đầu thu tín hiệu của chảo ăng-ten đặt tại tiêu điểm F của (P). Tính khoảng cách từ điểm M(0,25; 0,25) trên ăng-ten đến F.

 Xem đáp án
Xem đáp án
Hướng dẫn giải
Có 2p = 0,25 => p = 0,125 => p/2 = 0,0625.
Khoảng cách từ điểm M(0,25; 0,25) trên ăng-ten đến F bằng khoảng cách từ M đến đường chuẩn hay x + 0,0625 = 0 của parabol:
Câu 8:
17/07/2024Tìm tọa độ tiêu điểm và phương trình đường chuẩn của các parabol sau:
a) (P1): = 7x;
b) ;
c) .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Có 2p = 7 => p = 7/2 => p/2 = 7/4
=> Toạ độ tiêu điểm của parabol là F(7/4;0) phương trình đường chuẩn của parabol là x + 7/4 = 0
b) Có 2p = 1/3 => p = 1/6 => p/2 = 1/12
=> Toạ độ tiêu điểm của parabol là F(1/12;0), phương trình đường chuẩn của parabol là x + 1/12 = 0
a) Có 2p = => p = =>
=> Toạ độ tiêu điểm của parabol là F phương trình đường chuẩn của parabol là
Câu 9:
21/07/2024Tính bán kính qua tiêu của điểm đã cho trên các parabol sau:
a) Điểm M1(3; –6) trên (P1): = 12x;
b) Điểm M2(6; 1) trên ;
c) Điểm trên .
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Có 2p = 12, suy ra p = 6.
Bán kính qua tiêu của M1 là: FM1 = x + p/2 = 3 + 6/2 = 6.
b) Có 2p = 1/6 suy ra p = 1/12
Bán kính qua tiêu của M2 là: FM2 = x + p/2 = 6 + 1/24 = 145/24
b) Có 2p = suy ra p =
Bán kính qua tiêu của M3 là: FM3 = x + p/2 = + =
Câu 10:
20/07/2024Trong mặt phẳng Oxy, cho điểm A(1/4; 0) và đường thẳng d: x+1/4. Viết phương trình của đường (P) là tập hợp tâm M(x; y) của các đường tròn (C) di động nhưng luôn luôn đi qua A và tiếp xúc với d.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Có MA =
Khoảng cách từ M đến d là: d(M; d) =
Đường tròn (C) luôn đi qua A và tiếp xúc với d => MA = d(M; d)
Vậy (P) là một parabol có phương trình = 8x.
Câu 11:
18/07/2024Cho parabol (P). Trên (P) lấy hai điểm M, N sao cho đoạn thẳng MN đi qua tiêu điềm F của (P). Chứng minh rằng khoảng cách từ trung điểm I của đoạn thẳng MN đến đường chuẩn Δ của (P) bằng 1/2 MN và đường tròn đường kính MN tiếp xúc với Δ.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Giả sử parabol (P) có phương trình chính tắc là = 2px (p > 0).
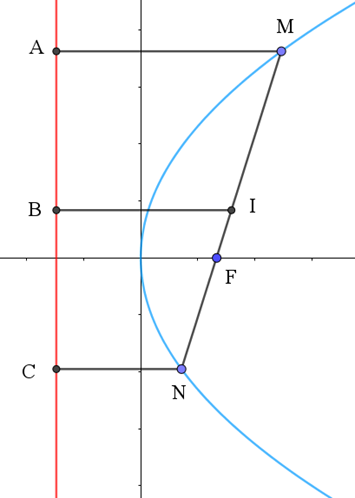
Gọi A, B, C lần lượt là hình chiếu của M, I, N lên Δ.
Vì I là trung điểm của MN nên IB là đường trung bình của hình thang MACN
=> Đường tròn đường kính MN chính là đường tròn tâm I, bán kính IB
Lại có Δ vuông góc với IB tại B
=> đường tròn đường kính MN tiếp xúc với Δ tại B.
Câu 12:
07/07/2024Hãy so sánh bán kính qua tiêu của điểm M trên parabol (P) với bán kính của đường tròn tâm M, tiếp xúc với đường chuẩn của (P).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Giả sử parabol (P) có phương trình chính tắc là = 2px (p > 0).
Gọi toạ độ của M là (x; y).
F(p/2;0) là tiêu điểm của (P), H là hình chiếu của M lên đường chuẩn Δ: x + p/2 = 0 của (P).
Khi đó:
MF =
MH =
Vậy MF = MH, mặt khác MH chính là bán kính của đường tròn tâm M, tiếp xúc với đường chuẩn của (P), do đó bán kính qua tiêu của điểm M trên parabol (P) bằng bán kính của đường tròn tâm M, tiếp xúc với đường chuẩn của (P).
Câu 13:
16/07/2024Một sao chổi A chuyển động theo quỹ đạo có dạng một parabol (P) nhận tâm Mặt Trời là tiêu điểm. Cho biết khoảng cách ngắn nhất giữa sao chổi A và tâm Mặt Trời là khoảng 112 km.
a) Viết phương trình chính tắc của parabol (P).
b) Tính khoảng cách giữa sao chổi A và tâm Mặt Trời khi sao chổi nằm trên đường thẳng đi qua tiêu điểm và vuông góc với trục đối xứng của (P).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
a) Chọn hệ trục toạ độ sao cho gốc toạ độ O trùng với đỉnh của parabol, tâm Mặt Trời trùng với tiêu điểm của parabol, đơn vị trên các trục là kilômét.
Gọi phương trình chính tắc của (P) là = 2px (p > 0).
Gọi F là tiêu điêm của (P), (x; y) là toạ độ của sao chổi A.
Khi đó khoảng cách giữa sao chổi A và tâm Mặt Trời là AF = ≥ p/2 (vì x ≥ 0)
=> khoảng cách ngắn nhất giữa sao chổi A và tâm Mặt Trời là p/2 (km)
=>
Vậy phương trình chính tắc của (P) là y2 = 448x.
b) Khi sao chổi nằm trên đường thẳng đi qua tiêu điểm và vuông góc với trục đối xứng của (P) thì sao chổi có hoành độ là x=p/2
Khoảng cách giữa sao chổi A và tâm Mặt Trời khi đó là:
AF = (km).
Câu 14:
22/07/2024Mặt cắt của gương phản chiếu của một đèn pha có dạng một parabol (P) có phương trình chính tắc = 6x. Tính khoảng cách từ điểm trên gương đến tiêu điểm của (P) (với đơn vị trên hệ trục toạ độ là xentimét).
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Có 2p = 6, suy ra p = 3.
Khoảng cách từ điểm trên gương đến tiêu điểm của (P) là:
MF = (cm).
