Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Trắc nghiệm Hình nón – Hình nón cụt – Diện tích xung quanh và thể tích có đáp án (Vận dụng)
-
678 lượt thi
-
10 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Cho hình thang vuông ABDC vuông tại A và B, biết cạnh AB = BC = 3m, AD = 5m. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh AB.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
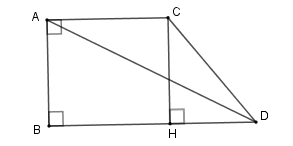
Xét tam giác vuông ABD ta có BD=√AD2-AB2=√52-32=4(cm).
Kẻ CH⊥BD tại H. Khi đó ACHB là hình vuông nên
CH=AB=AC=BH=3cm⇒HD=4-3=1cm.
Xét tam giác vuông CHD ta có CD2=CH2+HD2=32+12=10⇒CD=√10
Khi quay hình thang vuông ABDC quanh cạnh AB ta được hình nón cụt có bán kính đáy nhỏ AC, bán kính đáy lớn BD, đường sinh CD và chiều cao AB
Khi đó diện tích xung quanh hình nón cụt là
Sxq=π(R+r)l=π(3+4)√10=7π√10(cm2).
Câu 2:
11/11/2024Cho hình thang vuông ABCD vuông tại A và B, biết cạnh AB = BC = 4,5 cm, AD = 7,5cm. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh AB.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Lời giải
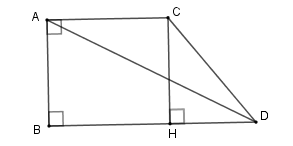
Xét tam giác vuông ABD ta có BD=√AD2-AB2=√7,52-4,52=6(cm).
Kẻ CH⊥BD tại H. Khi đó ACHB là hình vuông nên
CH=AB=AC=BH=4,5cm⇒HD=6-4,5=1,5cm.
Xét tam giác vuông CHD ta có CD2 = CH2 + HD2 = 4,52 + 1,52 = 22,5
CD = 3√102.
Khi quay hình thang vuông ABDC quanh cạnh AB ta được hình nón cụt có bán kính đáy nhỏ AC, bán kính đáy lớn BD, đường sinh CD và chiều cao AB
Khi đó diện tích xung quanh hình nón cụt là
Sxq=π(R+r)l=π(4,5+7,5)3√102=18π√10(cm2).
*Phương pháp giải:
Tính đáy BD và CD theo định lý Pytago
Sử dụng công thức diện tích xung quanh hình nón cụt Sxq=π(R+r)l.
*Lý thuyết:
Hình nón là hình được tạo ra khi quay tam giác vuông một vòng quanh một góc vuông cố định.
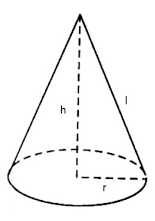
- Mặt đáy: là mặt phẳng có hình dạng hình chọn của hình nón.
- Đường cao: là khoảng cách từ tâm mặt đáy đến đỉnh của hình chóp hay được gọi là đường cao hạ từ đỉnh xuống tâm đáy hình nón. Được ký hiệu là: h.
- Đường sinh: là khoảng cách từ một điểm bất kỳ trên đường tròn đấy đến đỉnh của hình chóp. Được ký hiệu là: l.
- Bán kính đáy: là khoảng cách từ tâm đến một điểm trên hình tròn của mặt phẳng đáy. Được ký hiệu là: r.
Cho hình nón có bán kính đáy r và độ dài đường sinh l.
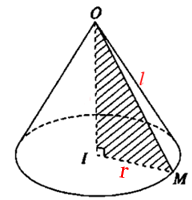
Khi đó:
Sxq = π.r.l
Xem thêm
Công thức tính diện tích xung quanh, diện tích toàn phần hình nón (2024) chính xác nhất
Câu 3:
16/07/2024Cho tam giác ABC đều cạnh a, đường trung tuyến AM. Quay tam giác ABC quanh cạnh AM. Tính diện tích toàn phần của hình nón tạo thành.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
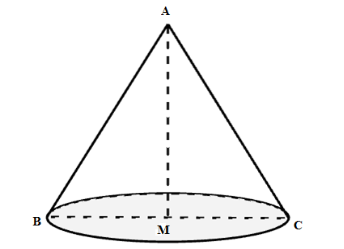
Xét tam giác ABC đều có AM vừa là đường trung tuyến, đường cao, đường phân giác nên ta có MC=BC2=a2.
Khi quay tam giác ABC quanh cạnh AM ta được hình nón đỉnh A, bán kính đáy là MC, đường sinh AC và chiều cao AM
Diện tích toàn phần của hình nón là:
Stp=πRl+πR2=π.MC.AC+π.MC2=π.a2.a+π(a2)2=3πa24.
Câu 4:
21/07/2024Cho tam giác ABC đều cạnh 4cm, đường trung tuyến AM. Quay tam giác ABC quanh cạnh AM. Tính diện tích toàn phần của hình nón tạo thành (đơn vị cm2).
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
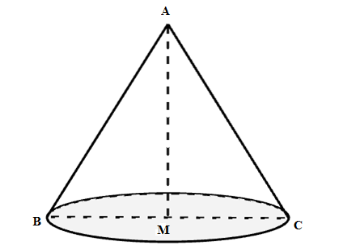
Xét tam giác ABC đều có AM vừa là đường trung tuyến, đường cao, đường phân giác nên ta có MC=BC2=42=2(cm).
Khi quay tam giác ABC quanh cạnh AM ta được hình nón đỉnh A, bán kính đáy là MC, đường sinh AC và chiều cao AM
Diện tích toàn phần của hình nón là:
Stp=πRl+πR2=π.MC.AC+π.MC2=π.2.4+π.22=12π(cm2).
Câu 5:
21/07/2024Cho một hình quạt tròn có bán kính 20cm và góc ở tâm là 144o. Người ta uốn hình quạt này thành một hình nón. Tính thể tích của khối nón đó.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D.
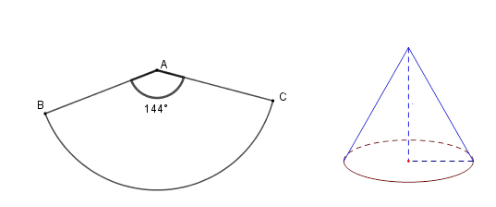
Ta uốn hình quạt BAC thành hình nón đỉnh A, đường sinh AB = 20cm
Khi đó độ dài cung BC chính là chu vi đáy của hình tròn
Ta có độ dài cung BC là lBC=π.20.144180=16π.
Khi đó chu vi đáy của hình nón C=2πR=16π⇒R=8cm.
⇒h2=l2-R2=202-82⇒h=4√21cm.
Thể tích khối nón V=13π.82.4√21=256π√213(cm3).
Câu 6:
22/07/2024Cho một hình quạt tròn có bán kính 12cm và góc ở tâm là 135o. Người ta uốn hình quạt này thành một hình nón. Tính thể tích của khối nón đó.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
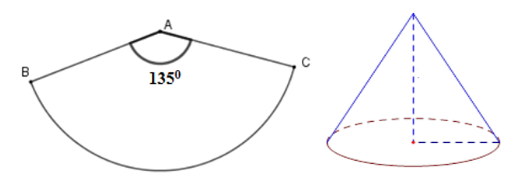
Ta uốn hình quạt BAC thành hình nón đỉnh A, đường sinh AB = 12cm
Khi đó độ dài cung BC chính là chu vi đáy của hình tròn
Ta có độ dài cung BC là lBC=π.12.135180=9π.
Khi đó chu vi đáy của hình nón C=2πR=9π⇒R=4,5cm.
⇒h2=l2-R2=122-4,52⇒h=3√552cm.
Thể tích khối nón V=13π.4,52.3√552=41π√558(cm3).
Câu 7:
18/07/2024Từ một khúc gỗ hình trụ cao 15cm, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là 640π . Tính thể tích khúc gỗ hình trụ.
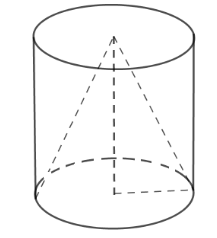
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Ta thấy hình nón có bán kính đáy bằng bán kính đáy hình trụ và chiều cao bằng chiều cao hình trụ nên
và Vt = 3Vn. Do đó phần gỗ bỏ đi chiếm thể tích khối trụ
Nên thể tích khối trụ là .
Câu 8:
23/07/2024Từ một khúc gỗ hình trụ cao 15cm, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là .
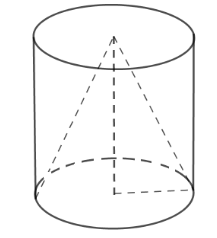
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Ta thấy hình nón có bán kính đáy bằng bán kính đáy hình trụ và chiều cao bằng chiều cao hình trụ nên
Vt = R2.h và Vn = R2h Vt = 3Vn. Do đó phần gỗ bỏ đi chiếm thể tích khối trụ
Nên thể tích khối trụ là Vt = 640 : = 960 (cm3)
Ta có Vt = R2h = 960 R2. 15 = 960 R = 8cm nên bán kính đáy của hình nón là R = 8cm
Chiều cao hình nón h = 15cm đường sinh hình nón l2 = h2 + R2 l = 17cm
Diện tích xung quanh hình nón là S = Rl = .8.17 = 136 (cm2)
Câu 9:
20/07/2024Từ một khúc gỗ hình trụ cao 24cm, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là 960 cm3.
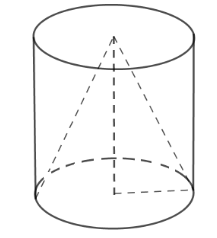
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Ta thấy hình nón có bán kính đáy bằng bán kính đáy hình trụ và chiều cao bằng chiều cao hình trụ nên
Vt = R2.h và Vn = R2h Vt = 3Vn. Do đó phần gỗ bỏ đi chiếm thể tích khối trụ
Nên thể tích khối trụ là Vt = 960 : = 1440 (cm3)
Câu 10:
20/07/2024Từ một khúc gỗ hình trụ cao 15cm, người ta tiện thành một hình nón (như hình vẽ). Biết phần gỗ bỏ đi có thể tích là . Tính diện tích xung quanh của hình nón.
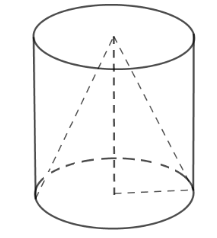
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Ta thấy hình nón có bán kính đáy bằng bán kính đáy hình trụ và chiều cao bằng chiều cao hình trụ nên
Vt = R2.h và Vn = .R2h Vt = 3Vn. Do đó phần gỗ bỏ đi chiếm thể tích khối trụ
Nên thể tích khối trụ là Vt = 960 : = 1440 (cm3)
Ta có Vt = R2.h = 1440R2. 24 = 1440 R = cm nên bán kính đáy của hình nón là R = cm, chiều cao hình nón h = 24cm
đường sinh hình nón l2 = h2 + R2 l = cm
Diện tích xung quanh hình nón là S = Rl = .. = (cm2).
Bài thi liên quan
-
Trắc nghiệm Toán 9 Bài 2 (có đáp án): Hình nón - Hình nón cụt - Diện tích xq và thể tích của hình
-
10 câu hỏi
-
20 phút
-
-
Trắc nghiệm Hình nón – Hình nón cụt – Diện tích xung quanh và thể tích có đáp án (Thông hiểu)
-
12 câu hỏi
-
25 phút
-
Có thể bạn quan tâm
- Bài 2: Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt (677 lượt thi)
Các bài thi hot trong chương
- Bài 1: Hình Trụ - Diện tích xung quanh và thể tích của hình trụ (703 lượt thi)
- Bài 3: Hình cầu. Diện tích mặt cầu và thể tích hình cầu (620 lượt thi)
- Đề kiểm tra Toán 9 Chương 4: Hình trụ - Hình nón - Hình cầu (271 lượt thi)
