Nội dung bài viết

    Xem thêm

    Chứng minh định lí: Trong các dây của một đường tròn, dây lớn nhất là đường kính

    Với giải câu hỏi 4 trang 126 sgk Toán lớp 9 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 743 04/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Ôn tập chương 2

    Câu hỏi 4 trang 126 Toán lớp 9 tập 1: Chứng minh định lí: Trong các dây của một đường tròn, dây lớn nhất là đường kính.

    Lời giải:

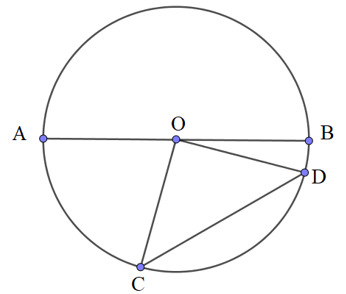
    Tài liệu VietJack

    Giả sử ta có đường tròn tâm O đường kính AB = 2R và một dây CD bất kì

    Ta cần chứng minh CD≤2R

    Nếu CD là đường kính thì CD = AB = 2R (1)

    Nếu CD không là đường kính, ta có:

    Xét tam giác COD

    Theo bất đẳng thức tam giác ta có: CD < OC + OD

    Mà OC = OD = R

    ⇒ CD < R + R⇒ CD < 2R (2)

    Từ (1) và (2) ta suy ra CD≤2R (đcpcm)

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 1 trang 126 Toán 9 Tập 1: Thế nào là đường tròn ngoại tiếp một tam giác...

    Câu hỏi 2 trang 126 Toán 9 Tập 1: Thế nào là đường tròn nội tiếp một tam giác...

    Câu hỏi 3 trang 126 Toán 9 Tập 1: Chỉ rõ tâm đối xứng của đường tròn...

    Câu hỏi 5 trang 126 Toán 9 Tập 1: Phát biểu các định lí về quan hệ vuông góc...

    Câu hỏi 6 trang 126 Toán 9 Tập 1: Phát biểu các định lí về liên hệ giữa dây và khoảng cách...

    Câu hỏi 7 trang 126 Toán 9 Tập 1: Nêu các vị trí tương đối của đường thẳng và đường tròn...

    Câu hỏi 8 trang 126 Toán 9 Tập 1: Phát biểu định nghĩa tiếp tuyến của đường tròn...

    Câu hỏi 9 trang 126 Toán 9 Tập 1: Nêu các vị trí tương đối của hai đường tròn...

    Câu hỏi 10 trang 126 Toán 9 Tập 1: Tiếp điểm của hai đường tròn tiếp xúc nhau...

    Bài 41 trang 128 Toán 9 Tập 1: Cho đường tròn (O) có đường kính BC...

    Bài 42 trang 128 Toán 9 Tập 1: Cho hai đường tròn (O) và (O’)...

    Bài 43 trang 128 Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; r)...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 743 04/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: