Nội dung bài viết

    Xem thêm

    Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài

    Với giải bài 42 trang 128 sgk Toán lớp 9 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 900 04/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Ôn tập chương 2

    Video Giải Bài 42 trang 128 Toán lớp 9 tập 1

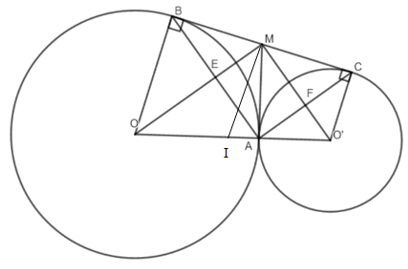
    Bài 42 trang 128 Toán lớp 9 tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, B∈ (O), C∈ (O’). Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O’M và AC. Chứng minh rằng:

    a) Tứ giác AEMF là hình chữ nhật.

    b) ME.MO = MF.MO’

    c) OO’ là tiếp tuyến của đường tròn có đường kính là BC.

    d) BC là tiếp tuyến của đường tròn có đường kính là OO’.

    Lời giải:

    Tài liệu VietJack

    a)

    Ta có: MB, MA là tiếp tuyến của đường tròn (O) nên MA = MB (tính chất hai tiếp tuyến cắt nhau) (1)

    Ta lại có MA, MC là tiếp tuyến của đường tròn (O’) nên MA = MC (tính chất hai tiếp tuyến cắt nhau) (2)

    Từ (1) và (2) suy ra MA = MB = MC

     ⇒MA=12BC

    Xét tam giác ABC

    Có MA là trung tuyến và MA=12BC

    Do đó, tam giác ABC vuông tại A

    ⇒^BAC=90o

    Xét tam giác MBA cân tại M  (do MA = MB )

    Có EM là phân giác nên ME cũng là đường cao

    ⇒ME⊥AB⇒^AEM=90o

    Xét tam giác MCA cân tại M (do MA = MC)

    Có FM là phân giác nên MF cũng là đường cao

    ⇒MF⊥AC⇒^AFM=90o

    Xét tứ giác AEMF có

    ^BAC=90o^AFM=90o^AEM=90o

    Do đó, AEMF là hình chữ nhật

    b)

    Xét tam giác AOM vuông tại A (do AM là tiếp tuyến)

    Có:

    AE⊥MO nên AE là đường cao.

    Áp dụng hệ thức lượng trong tam giác ta có:

    MA2=ME.MO (3)

    Xét tam giác AO’M vuông tại A (do AM là tiếp tuyến)

    Có AF⊥MO' nên AF là đường cao.

    Áp dụng hệ thức lượng trong tam giác ta có:

    MA2=MF.MO' (4)

    Từ (3) và (4) ⇒ ME. MO = MF. MO’

    c)

    Ta có MA = MB = MC (chứng minh câu a)

    Do đó, A, B, C nằm trên đường tròn tâm M bán kính MA

    Mặt khác OO'⊥MA tại A

    Do đó, OO’ là tiếp tuyến của đường tròn tâm M đường kính BC.

    d)

    Ta có: {OB⊥BCO'C⊥BC⇒OB//O'C

    Do đó, tứ giác OBCO’ là hình thang

    Gọi I là trung điểm của OO’.

    Ta có M là trung điểm của BC.

    Do đó, MI  là đường trung bình của hình thang OBCO’

    ⇒MI//OB//O'C

    Mà {OB⊥BCO'C⊥BC⇒MI⊥BC (5)

    Ta có AEMF là hình chữ nhật nên ^OMO'=^EMF=90o

    Do đó, tam giác OMO’ vuông tại M

    Ta lại có MI là trung tuyến của tam giác OMO’ nên MI = IO = IO’ (tính chất đường trung tuyến ứng với cạnh huyền)

    Do đó, O, M, O’ nằm trên đường tròn tâm I đường kính OO’ (6)

    Từ (5) và (6) ta suy ra BC là tiếp tuyến của đường tròn tâm I đường kính OO’.

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 1 trang 126 Toán 9 Tập 1: Thế nào là đường tròn ngoại tiếp một tam giác...

    Câu hỏi 2 trang 126 Toán 9 Tập 1: Thế nào là đường tròn nội tiếp một tam giác...

    Câu hỏi 3 trang 126 Toán 9 Tập 1: Chỉ rõ tâm đối xứng của đường tròn...

    Câu hỏi 4 trang 126 Toán 9 Tập 1: Chứng minh định lí: Trong các dây của một đường tròn...

    Câu hỏi 5 trang 126 Toán 9 Tập 1: Phát biểu các định lí về quan hệ vuông góc...

    Câu hỏi 6 trang 126 Toán 9 Tập 1: Phát biểu các định lí về liên hệ giữa dây và khoảng cách...

    Câu hỏi 7 trang 126 Toán 9 Tập 1: Nêu các vị trí tương đối của đường thẳng và đường tròn...

    Câu hỏi 8 trang 126 Toán 9 Tập 1: Phát biểu định nghĩa tiếp tuyến của đường tròn...

    Câu hỏi 9 trang 126 Toán 9 Tập 1: Nêu các vị trí tương đối của hai đường tròn...

    Câu hỏi 10 trang 126 Toán 9 Tập 1: Tiếp điểm của hai đường tròn tiếp xúc nhau...

    Bài 41 trang 128 Toán 9 Tập 1: Cho đường tròn (O) có đường kính BC...

    Bài 43 trang 128 Toán 9 Tập 1: Cho hai đường tròn (O; R) và (O’; r)...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 900 04/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: