Nội dung bài viết

    Xem thêm

    Cho nửa đường tròn đường kính AB cố định. C là một điểm trên

    Với giải câu hỏi 36 trang 106 sbt Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 460 29/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 9 Bài 6: Cung chứa góc

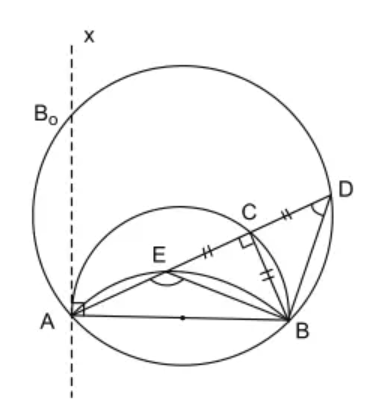
    Bài 36 trang 106 SBT Toán 9 Tập 2: Cho nửa đường tròn đường kính AB cố định. C là một điểm trên nửa đường tròn, trên dây AC kéo dài lấy điểm D sao cho CD = CB.

    a) Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.

    b) Trên tia CA lấy điểm E sao cho CE = CB. Tìm quỹ tích các điểm E khi C chạy trên nửa đường tròn đã cho.

    Lời giải:

    a)

    Chứng minh thuận

    Ta có: ACB^=90o  (góc nội tiếp chắn nửa đường tròn)

     ⇒BCD^=90o(kề bù)

    Xét tam giác BCD có:

     BCD^=90o(cmt)

    CD = CB (gt)

    Do đó, tam giác BCD vuông cân tại C

    ⇒CDB^=ADB^=45o

    AB cố định. Khi C chuyển động trên nửa đường tròn đường kính AB thì D chuyển động trên cung chứa góc 45o  dựng trên đoạn thẳng AB cố định.

    Ta có dây AC thay đổi phụ thuộc vào vị trí điểm C trên nửa đường tròn đường kính AB

    Dây AC lớn nhất bằng đường kính của đường tròn .Khi C trùng với B thì D cũng trùng với B. Vậy B là điểm của quỹ tích

    Dây AC nhỏ nhất có độ dài bằng 0 khi C trùng với A.Khi đó D trùng với B’ là giao điểm của tiếp tuyến đường tròn đường kính AB tại A với cung chứa góc 45° vẽ trên AB.

    Chứng minh đảo:

    Lấy điểm D’ bất kì trên cung lớn AB, nối AD’ cắt đường tròn đường kính AB tại C’. Nối BC’, B’D’.

    Ta có:  AD'B^=45o(vì D’ nằm trên cung chứa góc 45° vẽ trên AB)

    Xét đường tròn đường kính AB có:

     AC'B^=90o (góc nội tiếp chắn nửa đường tròn)

     ⇒BC'D'^=90o (kề bù)

    Xét tam giác tam giác BC’D’ có:

    AD'B^=C'D'B^=45o

    BC'D'^=90o

    Do dó, tam giác BC’D’ vuông cân tại C’

    ⇒C’B = C’D’

    Vậy quỹ tích điểm các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là cung BB’ nằm trên cung chứa góc 45° vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C.

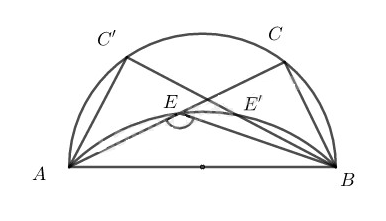
    b)

    Chứng minh thuận:

    Xét đường tròn đường kính AB có:

    Ta có:  ACB^=90o (góc nội tiếp chắn nửa đường tròn)

    Xét tam giác CBE có:

    ACB^=ECB^=90o

    CB = CE (gt)

    Do đó, tam giác CBE vuông cân tại C

    ⇒CEB^=45o

    Mà: CEB^+AEB^=180o  (hai góc kề bù)

    ⇒AEB^=135o

    Khi C chuyển động trên đường tròn đường kính AB cố định thì E chuyển động trên cung chứa góc 135° dựng trên đoạn thẳng AB cố định.

    Khi dây AC có độ dài lớn nhất bằng đường kính đường tròn thì C trùng với B nên E cũng trùng với B.vậy B là một điểm của quỹ tích

    Khi dây AC có độ dài nhỏ nhất bằng 0 thì C trùng với A. khi đó E trùng với A nên A là một điểm của quỹ tích.

    Vậy E chuyển động trên cung chứa góc 135° vẽ trên đoạn AB nằm trên nửa mặt phẳng bờ AB chứa điểm C.

    Chứng minh đảo:

    Lấy điểm E’ bất kì trên cung chứa góc 135°, nối AE’ cắt đường tròn đường kính AB tại C’. Nối BE’, B’C’.

    Ta có: AE'B^=135o  (vì E’ nằm trên cung chứa góc  vẽ trên AB)

    Lại có: AE'B^+BE'C^=180o  (hai góc kề bù)

    ⇒BE'C'^=180o−AE'B^=180o−135o=45o

    Xét đường tròn đường kính AB ta có:

     AC'B^=90o(góc nội tiếp chắn nửa đường tròn)

    Xét tam giác E’C’B có:

     E'C'B^=AC'B^=90o (cmt)

     BE'C'^=45o (cmt)

    Do đó, tam giác E’C’B vuông cân tại C’

    ⇒C'E'=C'B

    Quỹ tích điểm các điểm E khi C chuyển động trên nửa đường tròn đường kính AB là cung chứa góc 135° vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C.

    Xem thêm lời giải sách bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 33 trang 105 SBT Toán 9 Tập 2: Cho tam giác ABC có cạnh BC cố định...

    Câu hỏi 34 trang 105 SBT Toán 9 Tập 2: Dựng cung chứa góc...

    Câu hỏi 35 trang 106 SBT Toán 9 Tập 2: Dựng tam giác ABC biết BC = 3cm...

    Câu hỏi 37 trang 106 SBT Toán 9 Tập 2: Cho nửa đường tròn đường kính AB...

    Câu hỏi 38 trang 106 SBT Toán 9 Tập 2: Dựng hình vuông ABCD...

    Bài tập bổ sung

    Câu hỏi 6.1 trang 106 SBT Toán 9 Tập 2: Dựng một cung chứa góc... 

    Câu hỏi 6.2 trang 106 SBT Toán 9 Tập 2: Cho đường tròn tâm O bán kính R...

    Câu hỏi 6.3 trang 106 SBT Toán 9 Tập 2: Cho tam giác ABC có ba góc nhọn...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 460 29/03/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: