Nội dung bài viết

    Xem thêm

    Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A

    Với giải bài tập 77 trang 169 sbt Toán lớp 9 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 1,269 17/11/2021
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 9 Bài 8: Vị trí tương đối của hai đường tròn (Tiếp theo)

    Bài 77 trang 169 SBT Toán lớp 9 Tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈(O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng:

    a) MNQP là hình thang cân.

    b) PQ là tiếp tuyến chung của hai đường tròn (O) và (O’).

    c) MN + PQ = MP + NQ.

    Lời giải:

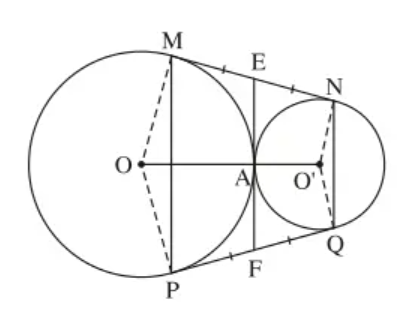
    Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A (ảnh 1)

    a)

    Vì M và P đối xứng qua trục OO’ nên OO’ là đường trung trực của MP

    ⇒ OP = OM

    Khi đó P thuộc (O) và MP ⊥ OO’    (1)

    Vì N và Q đối xứng qua trục OO’ nên OO’ là đường trung trực của NQ

    ⇒ O’N = O’Q

    Khi đó Q thuộc (O’) và NQ ⊥ OO’  (2)

    Từ (1) và (2) suy ra: MP // NQ

    Do đó, tứ giác MNPQ là hình thang

    Vì OO’ là đường trung trực của MP và NQ nên OO’ đi qua trung điểm hai đáy hình thang MNQP, OO’ đồng thời cũng là trục đối xứng của hình thang MNQP nên MNQP là hình thang cân.

    b)

    Ta có: MN ⊥ OM (tính chất tiếp tuyến)

    ⇒OMN^=90o⇒OMP^+PMN^=90o (3)

    Tam giác OMP cân tại O (do OM = OP)

    ⇒OPM^=OMP^ (4)

    Lại có MNQP là hình thang cân nên PMN^=QPM^ (5)

    Từ (3), (4), (5) ta suy ra OPM^+QPM^=90o⇒OPQ^=90o

    ⇒ QP ⊥ OP tại P

    Vậy PQ là tiếp tuyến của đường tròn (O).

    Ta có: MN ⊥ O’N (tính chất tiếp tuyến)

    ⇒O'NM^=90o⇒MNQ^−O'NQ^=90o (6)

    Tam giác O’NQ cân tại O’ (do O’N = O’Q)

    ⇒O'NQ^=O'QN^ (7)

    Lại có MNQP là hình thang cân nên MNQ^=PQN^ (8)

    Từ (6), (7), (8) ta suy ra PQM^−O'QN^=90o⇒O'QP^=90o

    Suy ra: QP ⊥ O’Q tại Q

    c)

    Kẻ tiếp tuyến chung tại A cắt MN tại E và PQ tại F

    Trong đường tròn (O), theo tính chất hai tiếp tuyến cắt nhau, ta có:

    EM = EA và FP = FA

    Trong đường tròn (O’), theo tính chất hai tiếp tuyến cắt nhau, ta có:

    EN = EA và FQ = FA

    ⇒ EM = EA = EN = 12MN

    Và FP = FA = FQ =  12PQ

    Suy ra : MN + PQ = 2EA + 2FA

    = 2(EA + FA) = 2EF    (9)

    E là trung điểm của MN (do EM = EN) và F là trung điểm của PQ (do FP = FQ)

    Do đó, EF là đường trung bình của hình thang MNQP nên :

    EF = 12 (MP + NQ) hay MP + NQ = 2EF    (10)

    Từ (9) và (10) suy ra: MN + PQ = MP + NQ

    Xem thêm lời giải sách bài tập Toán lớp 9 hay, chi tiết khác:

    Bài 71 trang 168 SBT Toán lớp 9 Tập 1: Cho I là trung điểm của đoạn thẳng AB...

    Bài 72 trang 169 SBT Toán lớp 9 Tập 1: Cho hai đường tròn đồng tâm O...

    Bài 73 trang 169 SBT Toán lớp 9 Tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A...

    Bài 74 trang 169 SBT Toán lớp 9 Tập 1: Cho hai đường tròn đồng tâm O...

    Bài 75 trang 169 SBT Toán lớp 9 Tập 1: Cho đường tròn (O ; 3cm) và đường tròn (O’; 1cm) tiếp xúc ngoài tại A...

    Bài 76 trang 169 SBT Toán lớp 9 Tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A...

    Bài 78 trang 170 SBT Toán lớp 9 Tập 1: Cho hai đường tròn (O; 2cm), (O’; 3cm), OO’ = 6cm...

    Bài 79 trang 170 SBT Toán lớp 9 Tập 1: Cho đường tròn (O; R), điểm A nằm bên ngoài đường tròn (R < OA < 3R)...

    Bài 80 trang 170 SBT Toán lớp 9 Tập 1: Cho đường tròn (O; 2cm) tiếp xúc với đường thẳng d...

    Bài tập bổ sung:

    Bài 8.1 trang 170 SBT Toán lớp 9 Tập 1: Cho hai đường tròn (O;R) và (O’;r). Điền vào chỗ trống của bảng sau...

    Bài 8.2 trang 170 SBT Toán lớp 9 Tập 1: Cho hai đường tròn (O; 3cm) và (O’; 4cm) có OO’ = 5cm...

    Bài 8.3 trang 171 SBT Toán lớp 9 Tập 1: Cho đường tròn (O) và điểm A cố định trên đường tròn...

     

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,269 17/11/2021
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: