Nội dung bài viết

    Xem thêm

    Cho ba hàm số: y = 1/2.x^2; y = x^2; y = 2x^2. Vẽ đồ thị của ba hàm số này

    Với giải bài 5 trang 37 sgk Toán lớp 9 Tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 9. Mời các bạn đón xem:

    1 1,114 05/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Bài 2: Đồ thị hàm số y = ax2 (a ≠ 0)

    Video Giải Bài 5 trang 37 SGK Toán 9 Tập 2

    Bài 5 trang 37 SGK Toán 9 Tập 2: Cho ba hàm số: y=12x2; y=x2; y=2x2.

    a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.

    b) Tìm ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.

    c) Tìm ba điểm A’; B’; C’ có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A’; B và B’; C và C’.

    d) Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.

    Lời giải

    a) Bảng giá trị tương ứng của x và y:

    x

    -2

    -1

    0

    1

    2

    y =12x2

    2

    		  

    0

    		  

    0

     

    x

    -2

    -1

    0

    1

    2

    y =x2

    4

    1

    0

    1

    4

     

    x

    -2

    -1

    0

    1

    2

    y =2x2

    8

    2

    0

    2

    8

    Ta vẽ các đồ thị hàm số (1): y=12x2; (2): y=x2; (3): y=2x2

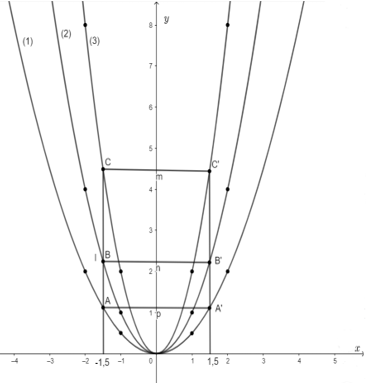
    Tài liệu VietJack

    b) Từ điểm (-1,5;0) nằm trên trục hoành ta kẻ đường thẳng song song với Oy. Đường thẳng này cắt các đồ thị (1); (2); (3) lần lượt tại các điểm A, B, C.

    Gọi yA,yB,yC lần lượt là tung độ của các điểm A, B, C. Ta có:

    yA=12.−1,52=12.94=98yB=1.−1,52=1.94=94yC=2.−1,52=2.94=92

    Vậy tung độ điểm A là 98; tung độ điểm B là 94; tung độ điểm C là 92.

    c) Từ điểm (1,5; 0) nằm trên trục hoành ta kẻ đường thẳng song song với Oy. Đường thẳng này cắt các đồ thị (1); (2); (3) lần lượt tại các điểm A’, B’, C’.

    Gọi lần lượt là tung độ của các điểm A’, B’,C’. Ta có:

    yA'=12.1,52=12.94=98yA'=1.1,52=1.94=94yA'=2.1,52=2.94=92

    Khi đó A’32;98; B’32;94; C'32;92

    Nhận xét: A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy.

    d) Hàm số có giá trị nhỏ nhất khi và chỉ khi y nhỏ nhất.

    Dựa vào đồ thị nhận thấy cả ba hàm số đạt y nhỏ nhất tại điểm O(0; 0).

    Vậy ba hàm số trên đều đạt giá trị nhỏ nhất tại x = 0.

    Xem thêm lời giải bài tập Toán lớp 9 hay, chi tiết khác:

    Câu hỏi 1 trang 34 Toán 9 Tập 2: Hãy nhận xét một vài đặc điểm của đồ thị này bằng cách trả lời các câu hỏi sau...

    Câu hỏi 2 trang 34 Toán 9 Tập 2: Nhận xét một vài đặc điểm của đồ thị và rút ra những kết luận...

    Câu hỏi 3 trang 35 Toán 9 Tập 2: Cho hàm số...

    Bài 4 trang 36 Toán 9 Tập 2: Cho hai hàm số...

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,114 05/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: