Câu hỏi:
22/07/2024 217Tìm T=∫xn1+x+x22!+x33!+...+xnn!dx?
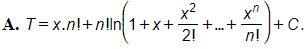
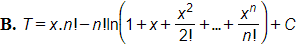
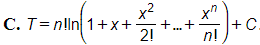
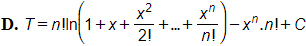
Đáp án chính xác
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: D
Giải thích:
Lời giải:
Điều kiện :
x−1x+1≥0⇔[x≥1x<−1
Trường hợp 1 : Nếu x≥1 thì
Q=∫√x−1x+1dx
=∫x−1√x2−1dx
=∫x√x2−1dx−∫1√x2−1dx
=√x2−1−ln|x+√x2−1|+C
Trường hợp 2: Nếu x<−1 thì
Q=∫√x−1x+1dx
=∫1−x√x2−1dx
=∫1√x2−1dx−∫x√x2−1dx
=ln|x+√x2−1|−√x2−1+C
Vậy đáp án đúng là đáp án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Kết quả nào dưới đây không phải là nguyên hàm của ∫(sin3x+cos3x)dx?
Xem đáp án »
23/07/2024
547


