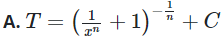Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: A
Giải thích:
Lời giải:
Ta có :
T=∫dxn√(xn+1)n+1
=∫dxxn+1.n√(1xn+1)n+1
=∫x−n−1(1xn+1)1+1ndx
=∫x−n−1(1xn+1)−1−1ndx
Đặt: t=1xn+1
⇒dt=−nxn+1=−nx−n−1
⇒T=−1n∫t−1−1ndt
=t−1n+C
+C
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Kết quả nào dưới đây không phải là nguyên hàm của ∫(sin3x+cos3x)dx?
Xem đáp án »
23/07/2024
542