Câu hỏi:
17/07/2024 203Tìm I=∫ex(3x−2)+√x−1√x−1(ex.√x−1+1)dx?
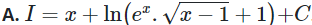
Đáp án chính xác
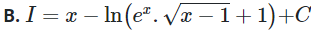
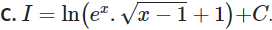
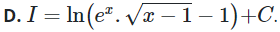
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: A
Giải thích:
Lời giải:
I=∫ex(3x−2)+√x−1√x−1(ex.√x−1+1)dx
=∫√x−1(ex.√x−1+1)+ex(2x−1)√x−1(ex.√x−1+1)dx
Đặt : t=ex.√x−1+1
⇒dt=(ex2√x−1+ex√x−1)dx
=ex(2x−1)2√x−1dx
Vậy ⇒I=∫dx+∫ex(2x−1)√x−1(ex√x−1+1)dx
=x+∫1tdt=x+ln|t|+C
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Kết quả nào dưới đây không phải là nguyên hàm của ∫(sin3x+cos3x)dx?
Xem đáp án »
23/07/2024
545


