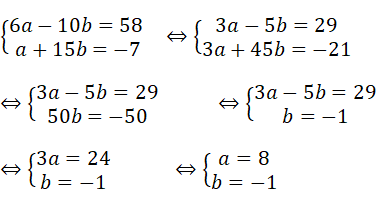Câu hỏi:
18/07/2024 184Tìm giá trị của a và b để hai đường thẳng () ∶(3a - 1)x + 2by = 56 và (:1/2 ax - (3b + 2)y = 3 cắt nhau tại điểm M(2; -5).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hai đường thẳng () và () cắt nhau tại M(2; -5) nên:
M ∈ ( ): + 2b.(-5) = 56 ⇔ 6a - 10b = 58
M ∈ ( ): 1/2 a.2 - (3b + 2)(-5) = 3 ⇔ a + 15b = -7
Khi đó, ta có hệ phương trình:
Vậy a = 8 và b = -1 thì hai đường thẳng ( ) và ( ) cắt nhau tại M(2; -5).