Câu hỏi:
22/07/2024 122
Mùa xuân ở hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún cây đu sẽ đưa người chơi dao động qua lại quanh vị trí cân bằng. Giả sử khoảng cách h (tính bằng mét) từ người chơi đu đến vị trí cân bằng được tính theo thời gian t (t ³ 0 và được tính bằng giây) bởi hệ thức h = |d| với , trong đó ta quy ước rằng d > 0 khi vị trí cân bằng ở về phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại.
a) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất.
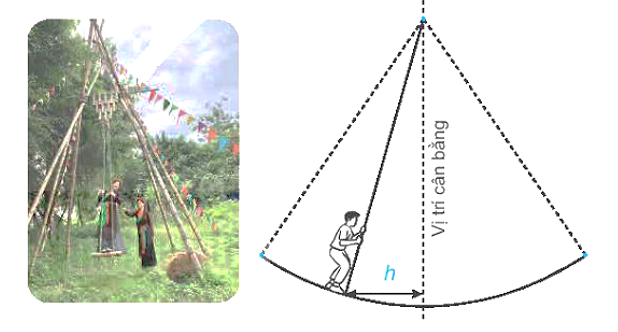
Mùa xuân ở hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún cây đu sẽ đưa người chơi dao động qua lại quanh vị trí cân bằng. Giả sử khoảng cách h (tính bằng mét) từ người chơi đu đến vị trí cân bằng được tính theo thời gian t (t ³ 0 và được tính bằng giây) bởi hệ thức h = |d| với , trong đó ta quy ước rằng d > 0 khi vị trí cân bằng ở về phía sau lưng người chơi đu và d < 0 trong trường hợp ngược lại.
a) Tìm các thời điểm trong vòng 2 giây đầu tiên mà người chơi đu ở xa vị trí cân bằng nhất.

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
a) Ta có h = |d| .
Vậy người chơi đu ở xa vị trí cân bằng nhất khi và chỉ khi , k Î ℤ.
Mà t Î [0; 2] nên , mà k Î ℤ nên k = 0; k = 1.
Với k = 0 thì t = (giây), k = 1 thì t = 2 (giây).
Vậy có 2 thời điểm t = giây và t = 2 giây người chơi đu ở xa vị trí cân bằng nhất.
a) Ta có h = |d| .
Vậy người chơi đu ở xa vị trí cân bằng nhất khi và chỉ khi , k Î ℤ.
Mà t Î [0; 2] nên , mà k Î ℤ nên k = 0; k = 1.
Với k = 0 thì t = (giây), k = 1 thì t = 2 (giây).
Vậy có 2 thời điểm t = giây và t = 2 giây người chơi đu ở xa vị trí cân bằng nhất.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một máy bay có 4 động cơ trong đó 2 động cơ ở cánh phải và 2 động cơ ở cánh trái. Chuyến bay hạ cánh an toàn khi trên mỗi cánh của nó có ít nhất một động cơ không bị lỗi. Giả sử mỗi động cơ ở cánh phải có xác suất bị lỗi là 0,01 và mỗi động cơ ở cánh trái có xác suất bị lỗi là 0,015. Các động cơ hoạt động độc lập với nhau. Tính xác suất để chuyến bay hạ cánh an toàn.
Một máy bay có 4 động cơ trong đó 2 động cơ ở cánh phải và 2 động cơ ở cánh trái. Chuyến bay hạ cánh an toàn khi trên mỗi cánh của nó có ít nhất một động cơ không bị lỗi. Giả sử mỗi động cơ ở cánh phải có xác suất bị lỗi là 0,01 và mỗi động cơ ở cánh trái có xác suất bị lỗi là 0,015. Các động cơ hoạt động độc lập với nhau. Tính xác suất để chuyến bay hạ cánh an toàn.
Câu 2:
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp B.CMND bằng
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp B.CMND bằng
Câu 3:
Hai bạn Dũng và Cường tham gia một kì thi học sinh giỏi môn Toán. Xác suất để Dũng và Cường đạt giải tương ứng là 0,85 và 0,9. Tính xác suất để:
a) Có ít nhất một trong hai bạn đạt giải;
Hai bạn Dũng và Cường tham gia một kì thi học sinh giỏi môn Toán. Xác suất để Dũng và Cường đạt giải tương ứng là 0,85 và 0,9. Tính xác suất để:
a) Có ít nhất một trong hai bạn đạt giải;
Câu 4:
Hai bạn An và Bình tham gia một trò chơi độc lập với nhau. Xác suất để An và Bình giành giải thưởng tương ứng là 0,8 và 0,6. Xác suất để có ít nhất một bạn giành giải thưởng là
Hai bạn An và Bình tham gia một trò chơi độc lập với nhau. Xác suất để An và Bình giành giải thưởng tương ứng là 0,8 và 0,6. Xác suất để có ít nhất một bạn giành giải thưởng là
Câu 5:
Cho tứ diện OABC có OA = OB = OC = a, và .
a) Chứng minh rằng (OBC) ^ (ABC).
Cho tứ diện OABC có OA = OB = OC = a, và .
a) Chứng minh rằng (OBC) ^ (ABC).
Câu 7:
c) Xác định nồng độ ion hydrogen trong bia biết độ pH của bia là khoảng 4,5.
c) Xác định nồng độ ion hydrogen trong bia biết độ pH của bia là khoảng 4,5.
Câu 8:
Cho đồ thị ba hàm số mũ y = ax, y = bx và y = cx như trong hình vẽ dưới đây. Khẳng định nào sau đây là đúng?
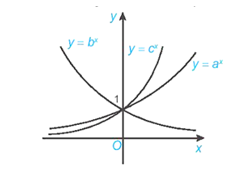
Cho đồ thị ba hàm số mũ y = ax, y = bx và y = cx như trong hình vẽ dưới đây. Khẳng định nào sau đây là đúng?

Câu 9:
Cho lăng trụ tam giác đều ABC.A'B'C' có AB = 1; AA' = 2. Thể tích khối lăng trụ ABC.A'B'C' bằng
Cho lăng trụ tam giác đều ABC.A'B'C' có AB = 1; AA' = 2. Thể tích khối lăng trụ ABC.A'B'C' bằng
Câu 10:
Hai bạn Sơn và Tùng, mỗi người gieo một con xúc xắc. Xác suất để số chấm xuất hiện trên cả hai con xúc xắc của Sơn và Tùng lớn hơn 1 là
Hai bạn Sơn và Tùng, mỗi người gieo một con xúc xắc. Xác suất để số chấm xuất hiện trên cả hai con xúc xắc của Sơn và Tùng lớn hơn 1 là
Câu 12:
Một chất điểm chuyển động có phương trình s(t) = t3 – 3t2 – 9t + 2, ở đó thời gian t > 0 tính bằng giây và quãng đường s tính bằng mét.
a) Tính vận tốc của chất điểm tại thời điểm t = 2 giây.
b) Tính gia tốc của chất điểm tại thời điểm t = 3 giây.
Một chất điểm chuyển động có phương trình s(t) = t3 – 3t2 – 9t + 2, ở đó thời gian t > 0 tính bằng giây và quãng đường s tính bằng mét.
a) Tính vận tốc của chất điểm tại thời điểm t = 2 giây.
b) Tính gia tốc của chất điểm tại thời điểm t = 3 giây.
Câu 13:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA ^ (ABC), . Khoảng cách từ A đến mặt phẳng (SBC) bằng
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA ^ (ABC), . Khoảng cách từ A đến mặt phẳng (SBC) bằng
Câu 14:
Giải các phương trình và bất phương trình sau
f) log (3x2 + 1) > log (4x).
Giải các phương trình và bất phương trình sau
f) log (3x2 + 1) > log (4x).


