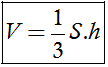Câu hỏi:
08/11/2024 373
Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng?
A. 4 mặt phẳng.
B. 1 mặt phẳng.
C. 2 mặt phẳng.
D. 3 mặt phẳng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
* Lời giải:
Hình hộp đứng có đáy là hình thoi (không phải là hình chữ nhật) có 3 mặt phẳng đối xứng bao gồm:
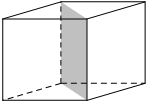
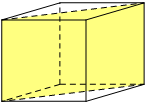
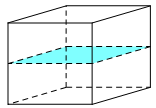
2 mặt phẳng chứa đường chéo của đáy và vuông góc với đáy.
Một mặt phẳng là mặt phẳng trung trực của cạnh bên.
* Phương pháp giải:
Hình hộp đứng
Định nghĩa. Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.
Tính chất. Hình hộp đứng có 2 đáy là hình bình hành, 4 mặt xung quanh là 4 hình chữ nhật.
* Lý thuyết cần nắm và các dạng toán về khối đa diện:
- Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy.
Khối chóp cụt là phần không gian được giới hạn bởi một hình chóp cụt kể cả hình chóp cụt ấy.
- Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy.
- Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay hình chóp giới hạn nó.
1. Hình lăng trụ đứng
Định nghĩa. Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với mặt đáy.
Tính chất. Các mặt bên của hình lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy.
2. Hình lăng trụ đều
Định nghĩa. Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.
Tính chất. Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau và vuông góc với mặt đáy.
• Hình hộp là hình lăng trụ có đáy là hình bình hành.
1. Hình hộp đứng
Định nghĩa. Hình hộp đứng là hình hộp có cạnh bên vuông góc với mặt đáy.
Tính chất. Hình hộp đứng có 2 đáy là hình bình hành, 4 mặt xung quanh là 4 hình chữ nhật.
2. Hình hộp chữ nhật
Định nghĩa. Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.
Tính chất. Hình hộp chữ nhật có 6 mặt là 6 hình chữ nhật.
3. Hình lập phương
Định nghĩa. Hình lập phương là hình hộp chữ nhật 2 đáy và 4 mặt bên đều là hình vuông
Tính chất. Hình lập phương có 6 mặt đều là hình vuông.
Hình chóp là hình có đáy là một đa giác và các mặt bên là các tam giác có chung một đỉnh.
THỂ TÍCH
1. Công thức tính thể tích khối chóp
Trong đó: S là diện tích đáy, h là chiều cao khối chóp.
2. Công thức tính thể tích khối lăng trụ
Trong đó: B là diện tích đáy, h là hiều cao khối lăng trụ
● Thể tích khối hộp chữ nhật: V = abc
Trong đó: a, b, c là ba kích thước của khối hộp chữ nhật.
● Thể tích khối lập phương: V = a3
Trong đó a là độ dài cạnh của hình lập phương.
TỈ SỐ THỂ TÍCH
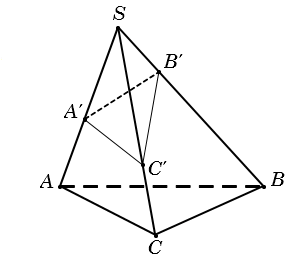
Cho khối chóp S.ABC và A', B', C' là các điểm tùy ý lần lượt thuộc SA, SB, SC ta có
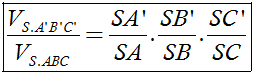
Phương pháp này được áp dụng khi khối chóp không xác đinh được chiều cao một cách dễ dàng hoặc khối chóp cần tính là một phần nhỏ trong khối chóp lớn và cần chú ý đến một số điều kiện sau
- Hai khối chóp phải cùng chung đỉnh.
- Đáy hai khối chóp phải là tam giác.
- Các điểm tương ứng nằm trên các cạnh tương ứng.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Khái niệm về khối đa diện (mới 2024 + Bài Tập) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Có tất cả bao nhiêu mặt phẳng cách đều bốn đỉnh của một tứ diện?
Câu 5:
Gọi lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối lập phương. Mệnh đề nào sau đây là đúng?
Câu 7:
Lắp ghép hai khối đa diện để tạo thành khối đa diện (H), trong đó là khối chóp tứ giác đều có tất cả các cạnh bằng a, là khối tứ diện đều cạnh a sao cho một mặt của trùng với một mặt của như hình vẽ. Hỏi khối da diện (H) có tất cả bao nhiêu mặt?
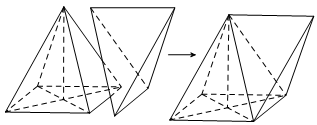
Lắp ghép hai khối đa diện để tạo thành khối đa diện (H), trong đó là khối chóp tứ giác đều có tất cả các cạnh bằng a, là khối tứ diện đều cạnh a sao cho một mặt của trùng với một mặt của như hình vẽ. Hỏi khối da diện (H) có tất cả bao nhiêu mặt?

Câu 9:
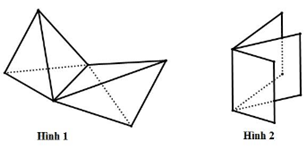
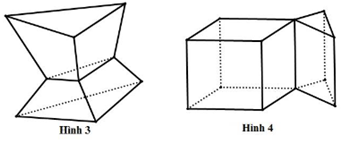
Cho các hình sau:
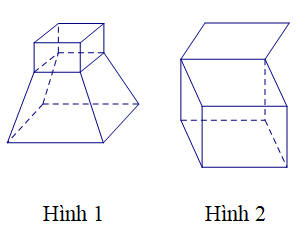
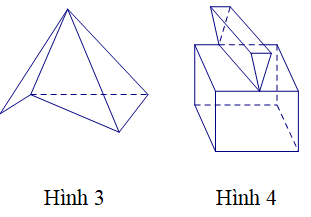
Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:
Cho các hình sau:


Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là: