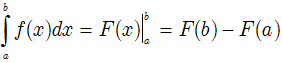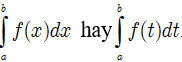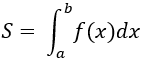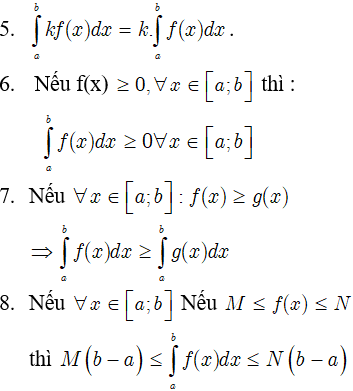Câu hỏi:
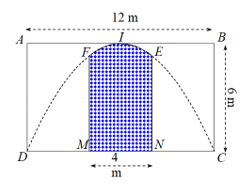
20/11/2024 3,342Một công ty quảng cáo X muốn làm một bức tranh trang trí hình ở chính giữa của một bức tường hình chữ nhật ABCD có chiều cao , chiều dài (hình vẽ bên). Cho biết là hình chữ nhật có ; cung có hình dạng là một phần của cung parabol có đỉnh I là trung điểm của cạnh AB và đi qua hai điểm C, D. Kinh phí làm bức tranh là 900.000 đồng/. Hỏi công ty X cần bao nhiêu tiền để làm bức tranh đó?
A. 20.400.000 đồng.
B. 20.600.000 đồng.
C. 20.800.000 đồng.
D. 21.200.000 đồng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Lời giải
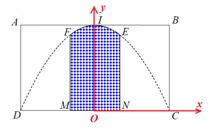
Gọi O là trung điểm MN. Chọn hệ trục tọa độ Oxy như hình vẽ.
Khi đó, ta có phương trình đường parabol đỉnh và đi qua hai điểm là
Diện tích bức tranh là diện tích hình phẳng giới hạn bởi đường parabol (P) trục Ox và hai đường thẳng . Khi đó
Vậy, số tiền công ty X cần dùng để làm bức tranh là
(đồng)
*Phương pháp giải:
Bước1:Viết phương trình parabol đi qua 2 điểm C và D
Bước2:Tính diện tích bức tranh giới hạn bởi Parabol và 2 đường thẳng x=2;x=-2
Bước3: Tính số tiền cần để làm bức tranh
*Lý thuyết:
Dựa vào các dữ kiện đề bài ta suy ra các yếu tố sau:
Parabol có tiêu điểm là F và đường chuẩn Δ:
Từ đó tìm được p, thay vào phương trình chính tắc của parabol là y2 = 2px (p > 0).
1. Khái niệm tích phân
* Định nghĩa:
Cho hàm số f liên tục trên K và a, b là hai số bất kì thuộc K. Nếu F là một nguyên hàm của f trên K thì hiệu số:
F(b) - F(a)
Được gọi là tích phân của f từ a đến b và kí hiệu:
* Nhận xét: Tích phân của hàm số f từ a đến b có thể kí hiệu bởi
Tích phân đó chỉ phụ thuộc vào f và các cận a; b mà không phụ thuộc vào cách ghi biến số.
* Định lí: Cho hàm số y = f(x) liên tục; không âm trên đoạn [a;b]. Khi đó, diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y = f(x); trục hoành và hai đường thẳng x = a; x = b là:
2. Tính chất của tích phân
Giả sử cho hai hàm số f(x) và g(x) liên tục trên K và a, b, c là ba số bất kỳ thuộc K. Khi đó ta có :

Xem thêm
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
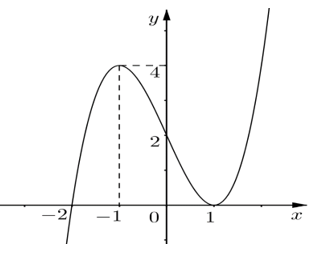
Cho hàm số đa thức bậc ba y=f(x)=ax3+bx2+cx+d (a≠0) có đồ thị như hình vẽ. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) và trục hoành.
Câu 2:
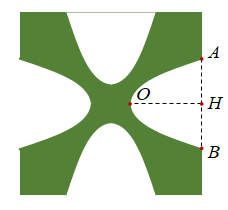
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng cm bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết cm, cm. Tính diện tích bề mặt hoa văn đó.
Câu 5:
Để tính ∫xln(2+x)dx theo phương pháp nguyên hàm từng phần, ta đặt
Câu 6:
Cho đồ thị hàm số như hình vẽ bên.
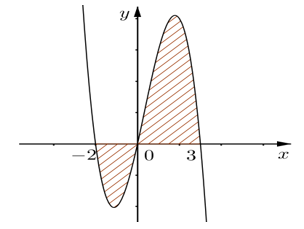
Diện tích S của hình phẳng phần tô đậm trong hình được tính theo công thức nào sau đây?
Câu 7:
Giả sử là hàm số liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K. Khẳng định nào sau đây sai?
Câu 8:
Diện tích hình phẳng S giới hạn bởi các đồ thị hàm số và trục hoành Ox (như hình vẽ) được tính bởi công thức nào dưới đây?
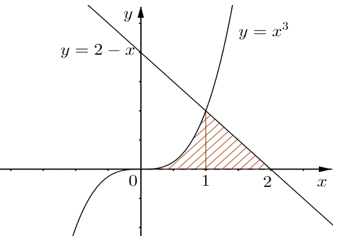
Câu 9:
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x thì được thiết diện là một hình chữ nhật có hai cạnh là 3x và .
Câu 11:
Cho hàm số f(x) xác định và liên tục trên [0;1] thỏa mãn . Giá trị
Câu 12:
Cho hình phẳng D giới hạn bởi đường cong và trục hoành. Tính thể tích V của khối tròn xoay tạo thành khi quay D quanh trục hoành.
Câu 14:
Cho F(x) là một nguyên hàm của hàm số . Biết F(1) =2. Giá trị của là
Câu 15:
Biết . Với là các số nguyên và tối giản. Trong các khẳng định sau khẳng định nào đúng?