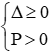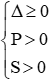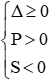Câu hỏi:
10/12/2024 381Có bao nhiêu số nguyên m thuộc sao cho phương trình có bốn nghiệm phân biệt?
A. 2020
B. 2018
C. 2016
D. 2020
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là B
Lời giải
Ta có:
Đặt . Ta có:
Khi đó phương trình trở thành (*) với
Để phương trình ban đầu có 4 nghiệm phân biệt thì phương trình (*) phải có 2 nghiệm t phân biệt thỏa mãn
Kết hợp điều kiện đề bài ta có
Vậy có 2020-3+1=2018 giá trị của m thỏa mãn yêu cầu bài toán
*Phương pháp giải:
Cho phương trình ax4 + bx2 + c = 0 (a ≠ 0) (1)
Đặt t = x2 (t ≥ 0), khi đó phương trình (1) trở thành: at2 + bt + c = 0 (2)
+ Để phương trình (1) có 4 nghiệm thì phương trình (2) có 2 nghiệm dương phân biệt
*Lý thuyết:
- Cho phương trình ax2 + bx + c = 0 (a ≠ 0). Khi đó
+ Điều kiện để phương trình có 2 nghiệm trái dấu: a.c < 0
+ Điều kiện để phương trình có 2 nghiệm cùng dấu:
( nếu là 2 nghiệm phân biệt cùng dấu ta thay ∆ ≥ 0 bởi ∆ > 0)
+ Điều kiện để phương trình có 2 nghiệm cùng dấu dương:
( nếu là 2 nghiệm phân biệt cùng dấu ta thay ∆ ≥ 0 bởi ∆ > 0)
+ Điều kiện để phương trình có 2 nghiệm cùng dấu âm:
( nếu là 2 nghiệm phân biệt cùng dấu ta thay ∆ ≥ 0 bởi ∆ > 0)
Xem thêm
Lý thuyết, cách xác định và bài tập các trường hợp phương trình có 2 nghiệm trái dấu
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho . Khi đó biểu thức với tối giản và . Tích a.b có giá trị bằng:
Câu 4:
Tìm tập hợp tất cả các tham số m sao cho phương trình có 4 nghiệm phân biệt.
Câu 5:
Có bao nhiêu số nguyên m để phương trình có hai nghiệm phân biệt lớn hơn 1.
Câu 6:
Hỏi có bao nhiêu giá trị m nguyên trong đoạn để phương trình có nghiệm duy nhất?
Câu 13:
Cho phương trình . Biết phương trình có 2 nghiệm phân biệt thỏa mãn . Giá trị của bằng:
Câu 14:
Cho các số thực a, b, c thuộc khoảng và thỏa mãn . Giá trị của biểu thức bằng:
Câu 15:
Biết rằng tập hợp các giá trị của m để phương trình có nghiệm, là với a, b là các số nguyên dương. Tính b – a.