Câu hỏi:
18/07/2024 178
Cho tứ diện ABCD có AB ^ CD và AC ^ BD. Gọi H là hình chiếu vuông góc của A xuống mặt phẳng (BCD). Chứng minh rằng H là trực tâm của ∆BCD và AD ⊥ BC.
Cho tứ diện ABCD có AB ^ CD và AC ^ BD. Gọi H là hình chiếu vuông góc của A xuống mặt phẳng (BCD). Chứng minh rằng H là trực tâm của ∆BCD và AD ⊥ BC.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
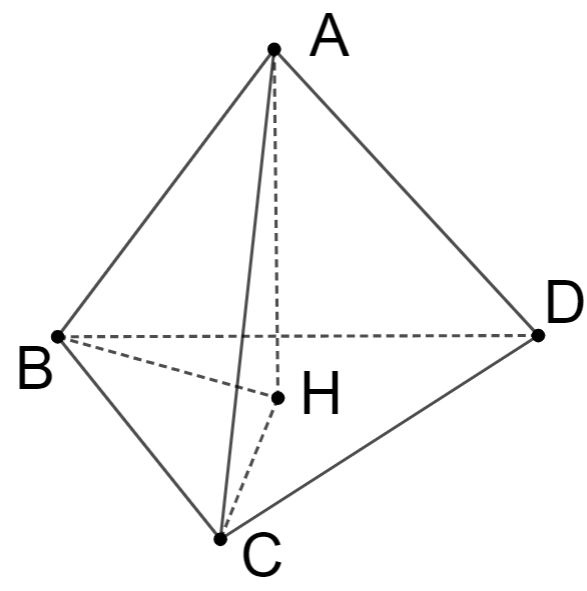
Theo giả thiết:
Suy ra CD ⊥ AHB
Do đó CD ⊥ BH (1)
Chứng minh tương tự: CH ⊥ BD (2)
Từ (1) và (2) suy ra H là trực tâm của ∆BCD.
Do đó DH ^ BC.
Lại có AH ^ BC suy ra BC ⊥ (AHD).
Vậy H là trực tâm của ∆BCD và AD ^ BC.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy là hình thoi, O là giao điểm của hai đường chéo, SA = SC, SB = SD.
a) Chứng minh rằng SO ^ (ABCD).
b) Gọi I, J lần lượt là trung điểm của BA, BC. Chứng minh rằng IJ ^ (SBD).
c) Chứng minh rằng BD ^ (SAC).
Cho hình chóp S.ABCD có đáy là hình thoi, O là giao điểm của hai đường chéo, SA = SC, SB = SD.
a) Chứng minh rằng SO ^ (ABCD).
b) Gọi I, J lần lượt là trung điểm của BA, BC. Chứng minh rằng IJ ^ (SBD).
c) Chứng minh rằng BD ^ (SAC).
Câu 2:
Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh . Biết rằng SA = SB = SC = SD, SO =
a) Chứng minh rằng SO ⊥ (ABCD).
b) Tính độ dài đường cao xuất phát từ đỉnh A của tam giác SAC.
Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh . Biết rằng SA = SB = SC = SD, SO =
a) Chứng minh rằng SO ⊥ (ABCD).
b) Tính độ dài đường cao xuất phát từ đỉnh A của tam giác SAC.
Câu 3:
Cho tứ diện ABCD có DA ⊥ (ABC), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ AH ⊥ MD tại H.
a) Chứng minh rằng AH ⊥ (BCD).
b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng GK ⊥ (ABC).
Cho tứ diện ABCD có DA ⊥ (ABC), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Vẽ AH ⊥ MD tại H.
a) Chứng minh rằng AH ⊥ (BCD).
b) Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Chứng minh rằng GK ⊥ (ABC).


