Câu hỏi:
22/07/2024 329Cho tập hợp A viết tập hợp B là tập con của A chỉ chứa các số hữu tỉ?
A = {4,2; 2,(531);\(\sqrt {10} \); \(2\frac{1}{3}\); \( - \sqrt {\frac{9}{4}} \)}
A. B = \(\left\{ {4,2;{\rm{ }}2,\left( {531} \right);{\rm{ }}\sqrt {10} ;{\rm{ }}\; - \sqrt {\frac{9}{4}} } \right\}\);
B. B = \(\left\{ {2,\left( {531} \right);{\rm{ }}\sqrt {10} ;{\rm{ }}2\frac{1}{3};\;{\rm{ }} - \sqrt {\frac{9}{4}} } \right\}\);
C. B = \(\left\{ {2\frac{1}{3};{\rm{ }}2,\left( {531} \right);{\rm{ }}4,2;{\rm{ }}\; - \sqrt {\frac{9}{4}} } \right\}\);
D. B = \(\left\{ {4,2;{\rm{ }}2,\left( {531} \right);{\rm{ }}2\frac{1}{3};\;{\rm{ }} - \sqrt {\frac{9}{4}} } \right\}\).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
Số hữu tỉ là số viết dưới dạng phân số \(\frac{a}{b}\)với \(a,b \in \mathbb{Z},b \ne 0\). Gồm các số thập phân hữu hạn và các số thập phân vô hạn tuần hoàn.
Ta có các số:
4,2 là số thập phân hữu hạn.
2,(531) là số thập phân vô hạn tuần hoàn.
\(\sqrt {10} = 3,162277...\) là số thập phân vô hạn không tuần hoàn.
\(2\frac{1}{3} = 2 + \frac{1}{3} = \frac{7}{3} = 2,(3)\)là số thập phân vô hạn tuần hoàn.
\( - \sqrt {\frac{9}{4}} = - \sqrt {{{(\frac{3}{2})}^2}} = - \frac{3}{2} = - 1,5\) là số thập phân hữu hạn.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
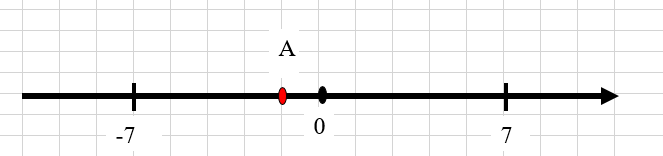
Cho hình dưới đây, hãy cho biết điểm A chỉ số thực nào? Biết điểm A màu đỏ chia 1 ô vuông nhỏ thành 3 phần bằng nhau.
Câu 3:
Cho một sợi dây dài 23 cm người ta muốn cắt ra thành những sợi dây ngắn hơn dài 3cm, hỏi sau khi cắt cắt được bao nhiêu sợi dây và sợi dây thừa ra dài khoảng bao nhiêu cm
Câu 4:
Sử dụng máy tính cầm tay tính \(\sqrt {94} \)và làm tròn đến chữ số thập phân thứ hai?
Câu 8:
Xác định tất cả giá trị của x để \(\left| {{x^2}} \right| = 49\)?
Câu 12:
Hãy so sánh \(\left| { - 1\frac{4}{5}} \right|\) và \(\left| {\frac{9}{5}} \right|\)?
Câu 13:
Cho tập hợp A viết tập hợp B là tập con của A chỉ chứa các số hữu tỉ?
\(A{\rm{ }} = {\rm{ }}\left\{ {3,4;{\rm{ }}1,\left( {231} \right);{\rm{ }}3\frac{5}{7};{\rm{ }}6,74283 \ldots ; - \sqrt {25} } \right\}\)
Câu 14:
Có bao nhiêu phần tử của tập hợp \(A = \{ x|x \in \mathbb{Z},81 \le \left| {{x^2}} \right| \le 144\)}??


