Câu hỏi:
23/07/2024 3,999Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 3:2. Khi đó bằng?
A. 3
B. 5
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
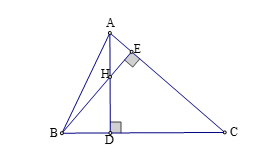
Xét tam giác vuông ABD và ADC, ta có: ;
Suy ra: (1)
Lại có (cùng phụ với ) và
Do đó (g.g), suy ra , do đó BD.DC = DH.AD (2)
Từ (1) và (2) suy ra (3)
Theo giả thiết suy ra hay , suy ra AD = HD
Thay vào (3) ta được:
Đáp án cần chọn là: D
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho tam giác ABC vuông tại A có AB = 9cm, tan C = . Tính độ dài cac đoạn thẳng AC và BC (làm tròn đến chữ số thập phân thứ hai)
Câu 3:
Cho tam giác ABC vuông tại A, đường cao AH có AB = 13cm, BH = 0,5dm. Tính tỉ số lượng giác sinC (làm tròn đến chữ số thập phân thứ 2)
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH có AC = 15cm, CH = 6cm. Tính tỉ số lượng giác cos B.
Câu 7:
Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H. Biết HD:HA = 1:2. Khi đó bằng?
Câu 8:
Cho tam giác ABC cân tại A có AB = AC = 13cm; BC = 10cm. Tính sin A
Câu 9:
Cho tam giác ABC vuông tại A có BC = 8cm, AC = 6cm. Tính tỉ số lượng giác tanC. (làm tròn đến chữ số thập phân thứ 2)
Câu 11:
Cho tam giác ABC vuông tại A có AB = 5cm, cot C = . Tính độ dài các đoạn thẳng AC và BC (làm tròn đến chữ số thập phân thứ 2)
Câu 12:
Cho tam giác vuông ABC vuông tại C có AC = 1cm, BC = 2cm. Tinh các tỉ số lượng giác sin B, cos B
Câu 13:
Cho tam giác ABC vuông tại A có BC = 9cm; AC = 5cm. Tính tỉ số lượng giác tan C (làm tròn đến chữ số thập phân thứ 1)
Câu 15:
Cho tam giác ABC vuông tại C có BC = 1,2cm, AC = 0,9cm. Tính các tỉ số lượng giác sinB và cosB.