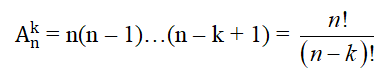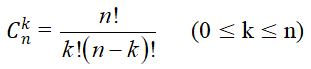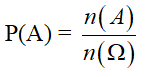Câu hỏi:
05/11/2024 4,133Cho một bảng ô vuông 3x3
Điền ngẫu nhiên các số 1, 2, 3, 4, 5, 6, 7, 8, 9 vào bảng trên (mỗi ô chỉ điền một số). Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”. Xác suất của A bằng:
A. P(A) =
B. P(A) =
C. P(A) =
D. P(A) =
Trả lời:
Giải bởi Vietjack
Đáp án đúng: B
*Lời giải:
Ta có 
Xét : Có ít nhất một hàng hoặc một cột chỉ toàn số chẵn.
Vì chỉ có 4 số chẵn là 2, 4, 6, 8 nên chỉ có thể có đúng một hàng hoặc đúng một cột chỉ toàn các số chẵn. Để điền như vậy cần chọn một trong số ba hàng hoặc ba cột rồi chọn 3 số chẵn xếp vào hàng hoặc cột đó, 6 số còn lại xếp tùy ý. Do đó 
Vậy 
*Phương pháp giải:
- tìm không gian mẫu
- tìm A ngang là" mỗi hàng hoặc mỗi cột sẽ có ít nhất 1 số chẵn"
- khi đó sẽ tính ra được xác suất cho biến cố A ngang. Và xác suất cho biến cố A sẽ = 1- P(Angang)
*Lý thuyến cần nắm về tổ hợp - xác suất
1. Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m+n cách thực hiện.
2. Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.
3. Hoán vị:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử.
- Số các hoán vị của n phần tử là: Pn = n(n-1)...2.1 = n!
4. Chỉnh hợp:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
- Số các chỉnh hợp chập k của n phần tử là:
5. Tổ hợp:
Giả sử A có n phần tử (n ≥ 1).
- Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).
Số các tổ hợp chập k của n phần tử là:
6. Công thức nhị thức Niu-tơn:
(a + b)n = Cn0an + Cn1an - 1b + … + Cnkan - kbk + … + Cnn-1abn-1 + Cnnbn
7. Phép toán trên các biến cố:
- Giả sử A là biến cố liên quan đến một phép thử.
Khi đó, tập Ω\A được gọi là biến cố đối của biến cố A, kí hiệu là A−.
- Giả sử A và B là hai biến cố liên quan đến một phép thử:
+ Tập A ⋃ B được gọi là hợp của các biến cố A và B.
+ Tập A ⋂ B được gọi là giao của các biến cố A và B.
+ Nếu A ⋂ B = ∅ thì ta nói A và B xung khắc.
8. Xác suất của biến cố:
Giả sử A là biến cố liên quan đến phép thử chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó, xác suất của biến cố A là: 
trong đó: n(A) là số phần tử của A; còn n(Ω) là số các kết quả có thể xảy ra của phép thử.
9. Tính chất của xác suất:
Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện.
P(∅) = 0, P(Ω) = 1
0 ≤ P(A) ≤ 1, với mọi biến cố A.
Nếu A và B xung khắc, thì P(AB) = P(A) + P(B) (công thức cộng xác suất)
Với mọi biến cố A, ta có: P(A−) = 1 – P(A).
A và B là hai biến cố độc lập khi và chỉ khi P(A.B) = P(A).P(B).
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Tổ hợp - xác suất hay, chi tiết
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho một đa giác đều 48 đỉnh. Lấy ngẫu nhiên 3 đỉnh của đa giác. Tính xác suất để tam giác tạo thành từ ba đỉnh đó là một tam giác nhọn.
Câu 2:
Trong chương trình giao lưu gồm có 15 người ngồi vào 15 ghế theo một hàng ngang. Giả sử người dẫn chương trình chọn ngẫu nhiên 3 người trong 15 người để giao lưu với khán giả. Xác suất để trong 3 người được chọn đó không có 2 người ngồi kề nhau là
Câu 3:
Gọi S là tập hợp các số tự nhiên có chín chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc tập S. Xác suất để số được chọn chia hết cho 3 là
Câu 4:
Cho tập hợp (S). Hai bạn A, B mỗi bạn chọn ngẫu nhiên một tập con của (S). Xác suất để tập con của A và B chọn được có đúng 2 phần tử chung gần nhất với kết quả nào dưới đây?
Câu 5:
Có 15 cuốn sách gồm 4 cuốn sách Toán, 5 cuốn sách Lý và 6 cuốn sách Hóa. Các cuốn sách đôi một khác nhau. Thầy giáo chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học sinh. Tính xác suất để số cuốn sách còn lại của thầy còn đủ 3 môn
Câu 6:
Cho một đa giác đều có 20 đỉnh nội tiếp trong đường tròn (C). Lấy ngẫu nhiên hai đường chéo trong số các đường chéo của đa giác. Tính xác suất để lấy được hai đường chéo cắt nhau và giao điểm của hai đường chéo trong đường tròn?
Câu 7:
Cho tập S = {1;2;3;...;19;20} gồm 20 số tự nhiên từ 1 đến 20. Lấy ngẫu nhiên ba số thuộc S. Xác suất để ba số lấy được lập thành một cấp số cộng là
Câu 8:
Trong một buổi dạ hội có 10 thành viên nam và 12 thành viên nữ, trong đó có 2 cặp vợ chồng. Ban tổ chức muốn chọn ra 7 đôi, mỗi đôi gồm 1 nam và 1 nữ để tham gia trò chơi. Tính xác suất để trong 7 đôi đó, có đúng một đôi là cặp vợ chồng. Biết rằng trong trò chơi, người vợ có thể ghép đôi với một người khác chồng mình và người chồng có thể ghép đôi với một người khác vợ mình
Câu 9:
Cho đa giác 30 đỉnh nội tiếp đường tròn, gọi (S) là tập hợp các đường thẳng đi qua hai trong số 30 đỉnh đã cho. Chọn 2 đường thẳng bất kỳ thuộc tập (S). Tính xác suất để chọn được 2 đường thẳng mà giao điểm của chúng nằm bên trong đường tròn.
Câu 10:
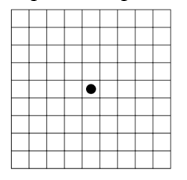
Cho một quân cờ đứng ở vị trí trung tâm của một bàn cờ 9x9 (xem hình vẽ). Biết rằng, mỗi lần di chuyển, quân cờ chỉ di chuyển sang ô có cùng một cạnh với ô đang đứng. Tính xác suất để sau bốn lần di chuyển, quân cờ không trở về đúng vị trí ban đầu.
Câu 11:
Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng , trong đó 1abcd9
Câu 12:
Gọi S là tập tất cả các số tự nhiên có 4 chữ số đôi một khác nhau được chọn từ các chữ số 1,2,3,4,5,6,7,8,9. Lấy ngẫu nhiên một số thuộc S. Tính xác suất để lấy được một số chia hết cho 11 và tổng 4 chữ số của nó cũng chia hết cho 11.
Câu 13:
Một nhóm học sinh gồm bốn bạn nam trong đó có bạn Quân và bốn bạn nữ trong đó có bạn Lan. Xếp ngẫu nhiên bốn bạn trên thành một hàng dọc. Xác suất để xếp được hàng dọc thỏa mãn các điều kiện: đầu hàng và cuối hàng đều là nam và giữa hai bạn nam gần nhau có ít nhất một bạn nữ, đồng thời bạn Quân và bạn Lan không đứng cạnh nhau bằng
Câu 14:
Gọi A là tập các số tự nhiên có 3 chữ số đôi một khác nhau. Lấy ngẫu nhiên ra từ A hai số. Tính xác suất để lấy được hai số mà các chữ số có mặt ở hai số đó giống nhau.
Câu 15:
Cho A là tập tất cả các số tự nhiên có 5 chữ số phân biệt. Chọn ngẫu nhiên một số từ tập tính xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1.
